Введение

Лист 160

Лист 159

Лист 158

Лист 157

Лист 156

Лист 155

Лист 154

Лист 153

ПЕРЕЧЕНЬ СТИХОТВОРЕНИЙ, ОПИСЫВАЮЩИХ ГРАФИЧЕСКИЙ ОБРАЗ БУКВЫ И ЕЁ ПРОСТОЕ ПОЛОЖЕНИЕ

Конверт №4

Конверт №3

Конверт №2

Конверт №1

БУКВ ИЗ ЭЛЕМЕНТОВ

КОНСТРУИРОВАНИЕ И РЕКОНСТРУИРОВАНИЕ

Лист 152

Лист 151

Лист 150

НАПИСАННЫХ БУКВ

ПРАВИЛЬНО И НЕПРАВИЛЬНО

УЗНАВАНИЕ

Лист 149

Лист 148

Лист 147

ДИФФЕРЕНЦИАЦИЯ ОПТИЧЕСКИ СХОДНЫХ БУКВ

Лист 146

Лист 145

Лист 144

Лист 143

Лист 142

Лист 141

Лист 140

Лист 139

Лист 138

Лист 137

Лист 136

Лист 135

Лист 134

Лист 133

Лист 132

Лист 131

Лист 130

Лист 129

Лист 128

Сигналы, используемые при моделировании, отладке и тестировании систем, относятся к классу детерминированных сигналов. Детерминированным называется сигнал, который можно полностью описать аналитической функцией, зависящей от времени или частоты. Детерминированные сигналы можно разделить на две большие группы: импульсные и периодические сигналы. Под импульсными понимаются сигналы, обладающие конечной энергией. При этом импульсные сигналы могут описываться как ограниченной во времени на заданном интервале функцией, так и бесконечной функцией. Периодические сигналы могут быть получены путем суммирования бесконечного числа импульсных сигналов, отстоящих друг от друга на одинаковый интервал времени, называемый периодом повторения сигнала. Периодические сигналы обладают бесконечной энергией и характеризуются средней мощностью за период.

Анализ сигналов в радиотехнических или электронных системах заключается в определении временных и частотных характеристик этих сигналов. К ним относятся временная функция сигнала, спектральная плотность или спектр сигнала, энергетический спектр или спектр мощности сигнала. По этим характеристикам можно определить параметры сигналов, главными из которых являются:

– длительность, период повторения (временные параметры);

– ширина спектра, положения максимумов спектра, положение частотных гармоник (частотные параметры);

– энергия сигнала, средняя мощность сигнала (энергетические, мощностные параметры).

Зная численные значения параметров сигналов можно проводить их сравнение между собой, а также оценивать их изменение при прохождении через радиотехническую или электронную систему.

Домашнее контрольное задание (ДКЗ) по дисциплине "Теория радиотехнических сигналов" посвящено решению задач расчета основных характеристик детерминированных сигналов на основе теории спектрального анализа. Его целью является систематизация и расширение теоретических знаний, приобретение практических навыков производства и оформления инженерных расчетов. Основой расчета является спектральный анализ периодических и непериодических сигналов с использованием ряда и интеграла Фурье.

Задача № 1. Спектральный анализ периодической последовательности прямоугольных видеоимпульсов в базисе тригонометрических функций кратного аргумента.

Необходимо:

1. Изобразить в масштабе график временного представления периодического колебания в соответствии с исходными данными предложенного варианта.

2. Записать общий вид ряда Фурье в 1 форме, пояснив значения коэффициентов, входящих в ряд.

3. Найти общие выражения для коэффициентов ряда и рассчитать их значения до к = 5. Результаты свести в таблицу.

4. Для полученных результатов записать ряд Фурье в первой форме.

5. Записать общий вид ряда Фурье во второй форме, пояснив физический смысл входящих в него коэффициентов.

6. Найти общие выражения для коэффициентов 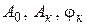и рассчитать их значения до пятой гармоники включительно. Результаты свести в таблицу.

7. Для полученных коэффициентов записать ряд Фурье во второй форме.

8. В масштабе построить графики спектров амплитуд и фаз. Сделать вывод об их характере. Пояснить понятие "огибающей" спектра амплитуд.

9. Дать определение энергетической ширины спектра амплитуд, раскрыть физическую сущность равенства Парсеваля.

10. Определить полную мощность сигнала и энергетическую ширину спектра при условии сохранения в нем заданного процента полной мощности.

11. Сделать выводы по проведенным инженерным расчетам.

Задача № 2. Спектральный анализ непериодического видеоимпульса.

Необходимо:

1. Получить аналитическую модель одиночного видеоимпульса заданной формы.

2. Изобразить в масштабе график временного представления исходного сигнала.

3. Привести общее выражение для определения спектральной плотности непериодического сигнала.

4. Найти спектр заданного непериодического сигнала (спектральную функцию, вещественную и мнимую части спектральной функции, амплитудный и фазовый спектры). Изобразить графики с использованием программных средств и дать их краткую характеристику.

5. Определить полную энергию видеоимпульса

6. Определить энергетическую ширину спектра F _э сигнала при условии сохранения в нем заданного в исходных данных процента полной энергии.

7. Восстановить сигнал по известному спектру в ограниченной полосе частот F _э с использованием программных средств, оценить точность восстановления.

8. Сделать выводы по проведенным инженерным расчетам, обратив внимание на связь ширины спектра с длительностью импульса.

На практике отыскание спектров импульсных сигналов непосредственно с помощью прямого преобразования Фурье часто приводит к значительным вычислительным трудностям. Для нахождения спектров удобнее воспользоваться известными спектрами сигналов простой формы и свойствами преобразования Фурье, представленными в приложениях 1 и 2 соответственно.

В общем случае последовательность действий при нахождении спектров сигналов с использованием теорем о свойствах преобразования Фурье следующая:

– выбрать из таблицы типовых сигналов (прил. 1) сигналы, с помощью которых можно сформировать заданный сигнал;

– записать заданный сигнал с помощью математических операций над выбранными типовыми сигналами;

– найти аналитическое выражение спектра заданного сигнала с использованием известных спектров типовых сигналов и теорем о свойствах спектров;

– выполнить проверку правильности нахождения спектра заданного сигнала с помощью свойств площади функций s (t) и 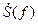, свойств симметрии сигнала и спектра.

Дата добавления: 2014-12-10