
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Рекомендации по решению задачи № 2
|
|
|
|
Импульсные сигналы в общем случае могут быть заданы своими моделями на конечном интервале времени [ t 1, t 2], полубесконечном интервале: (–∞, t 0], [ t 0, ∞). Примерами сигналов, ограниченных во времени, являются прямоугольный импульс, треугольный импульс и другие, а также любой сигнал, умноженный на функцию, ограниченную во времени на некотором интервале [ t 1, t 2]:
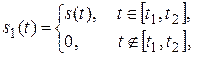
где s (t) – сигнал, определённый на более широком временном интервале, чем функция s 1(t). Примерами сигналов, определённых на бесконечных или полубесконечных интервалах, являются экспоненциальные функции, импульсы гауссовской формы (см. прил. 1), а также сигналы, образованные из указанных сигналов с помощью линейных операций: суммирование, взвешивание (умножение на амплитудный коэффициент), задержка и др.
В частотной области аналоговые импульсные сигналы можно описать с помощью спектральной функции (спектра) 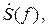 которая связана с временной функцией сигнала s (t) преобразованием Фурье. Прямое преобразование Фурье имеет вид:
которая связана с временной функцией сигнала s (t) преобразованием Фурье. Прямое преобразование Фурье имеет вид:

Спектр 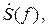 в общем случае является комплексной функцией частоты, которая обладает комплексно-сопряжённой симметрией для сигналов s (t), описываемых действительными функциями:
в общем случае является комплексной функцией частоты, которая обладает комплексно-сопряжённой симметрией для сигналов s (t), описываемых действительными функциями:
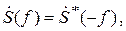
где «*» означает комплексное сопряжение, т.е. смену знака перед мнимыми составляющими комплексной функции  .
.
Любую комплексную функцию  можно представить в показательной форме через модуль и аргумент:
можно представить в показательной форме через модуль и аргумент:
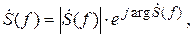
либо в квадратурной форме через действительную и мнимую части:
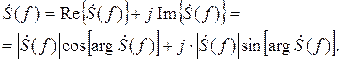
Модуль спектральной функции 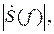 называемый амплитудным спектром (АС), представляет собой действительную функцию, обладающую свойством чётной симметрии:
называемый амплитудным спектром (АС), представляет собой действительную функцию, обладающую свойством чётной симметрии:
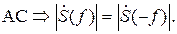
Аргумент спектральной функции 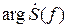 , называемый фазовым спектром (ФС), обладает свойством нечётной симметрии:
, называемый фазовым спектром (ФС), обладает свойством нечётной симметрии:
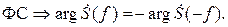
Аналогичными свойствами обладают действительная и мнимая части спектральной функции:
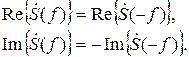
Показательная и квадратурная формы спектральной функции сигнала связаны между собой следующими соотношениями:


При отображении спектров сигналов удобно пользоваться следующими рекомендациями. Во-первых, спектр действительных сигналов всегда изображается в виде пары графиков (АС и ФС, либо действительная и мнимая части спектра), представляемых в одинаковом масштабе по оси частот. Во-вторых, при изображении спектров можно использовать только положительные частоты. В-третьих, ФС строится в пределах [–π, π] по вертикальной оси, поскольку добавление целого числа 2π к аргументу комплексной функции не изменяет её значения.
Таким образом, основными характеристиками аналогового импульсного сигнала являются временная s (t) и спектральная 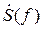 функция сигнала, связанные между собой преобразованием Фурье:
функция сигнала, связанные между собой преобразованием Фурье:
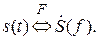
Для сравнения сигналов друг с другом используются параметры сигналов и спектров. Основными параметрами аналогового импульсного сигнала является его длительность τ и ширина спектра F. Они характеризуют размеры интервалов времени и частоты, в пределах которых сосредоточена основная часть энергии сигнала.
Геометрический смысл энергии сигнала заключается в величине площади под квадратом временной функции сигнала
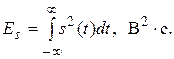
В соответствии с теоремой Парсеваля для аналоговых импульсных сигналов их энергию можно также определить по амплитудно-частотному спектру:
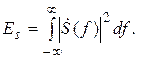
В том случае, когда сигнал имеет конечную длительность, ограниченную временным интервалом [ t 1, t 2], т.е. длительность сигнала равна τ = t 2 – t 1, его спектральная функция 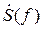 не ограничена на оси частот, поэтому ширину спектра F сигнала s (t) нужно выбирать, исходя из выбранного критерия. Введём понятие энергетической ширины спектра как интервала частот, в котором сосредоточена заданная доля общей энергии сигнала. В некоторых источниках используются термины эквивалентная или эффективная ширина спектра.
не ограничена на оси частот, поэтому ширину спектра F сигнала s (t) нужно выбирать, исходя из выбранного критерия. Введём понятие энергетической ширины спектра как интервала частот, в котором сосредоточена заданная доля общей энергии сигнала. В некоторых источниках используются термины эквивалентная или эффективная ширина спектра.
Если в спектре сигнала не наблюдается ярко выраженного максимума на некоторой частоте f 0, или этот максимум находится вблизи начала координат, то за начало интервала частот, определяющего энергетическую ширину спектра, принимают нулевую частоту. Такие аналоговые сигналы относятся к так называемым видеосигналам. Другим характерным свойством видеосигналов является отсутствие высокочастотного (как правило гармонического) " заполнения " сигнала, наблюдаемого у модулированных радиосигналов.
Если задаться долей энергии в пределах ширины спектра
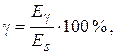
то эффективную ширину спектра F э можно косвенно определить из соотношения:
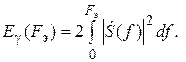
При определении энергетической ширины спектра удобно пользоваться графиком зависимости части энергии сигнала в полосе F э от ширины интервала частот [0, F э]. На рис. 2.2. показан пример такой зависимости.
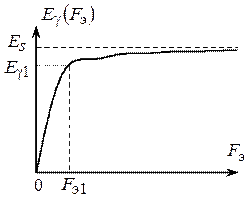
Рис. 2.2. Зависимость части энергии сигнала от ширины
интервала частот
Во временной области импульсный видеосигнал характеризуется эффективной длительностью τэ, которая определяется как длительность интервала времени, в котором сосредоточена заданная часть общей энергии сигнала. Если расположить начало координат в точке, соответствующей началу сигнала s (t), то эффективная длительность сигнала τэ косвенно находится из выражения

Обратное преобразование Фурье позволяет найти сигнал по его спектру:

Восстановление сигнала s (t) по известному спектру в ограниченной полосе частот F э даёт аппроксимацию сигнала:
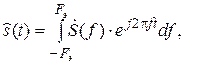
Отличие аппроксимации сигнала  от исходного сигнала s (t) в метрическом пространстве сигналов можно оценить по величине метрики
от исходного сигнала s (t) в метрическом пространстве сигналов можно оценить по величине метрики  или ее квадрата – энергии разности сигналов:
или ее квадрата – энергии разности сигналов:
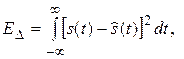
используемой в качестве меры точности восстановления сигнала.
Энергетическая ширина спектра F э и эффективная длительность τэ сигнала определяют интервалы по частоте и времени, в которых сосредоточена информация о форме сигнала и его спектра. Чем ближе параметр γ к 100%, тем точнее сохраняется форма сигнала и его спектра при переходе из частотной области во временную область и обратно с помощью интеграла Фурье с ограниченными пределами.
Помимо временной и спектральной функций в качестве характеристики детерминированных импульсных сигналов используют также энергетический спектр Ws (f).
Энергетический спектр импульсного сигнала s (t) определяется следующим образом:
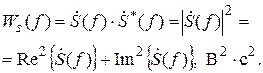
Важно отметить, что в энергетическом спектре отсутствует информация о фазовом спектре сигнала, поэтому по энергетическому спектру нельзя восстановить спектральную 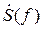 или временную s (t) функции сигнала. Энергетический спектр является действительной функцией и обладает чётной симметрией, поэтому его можно изобразить в виде одного графика W 0 (f) =2 Ws (f) в области положительных частот.
или временную s (t) функции сигнала. Энергетический спектр является действительной функцией и обладает чётной симметрией, поэтому его можно изобразить в виде одного графика W 0 (f) =2 Ws (f) в области положительных частот.
По энергетическому спектру Ws (f) детерминированного импульсного сигнала можно определить ширину его спектра F.
Рассмотрим несколько примеров спектрального анализа одиночных видеоимпульсов.
Пример 2.1
Найдем спектр аналогового экспоненциального импульсного сигнала, который задается выражением
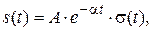
где σ(t) – единичная ступенчатая функция (функция Хевисайда):
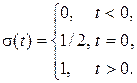
График функции сигнала s (t) при выбранных значениях параметров А = 3 В и α = 3,14 1/мкс показан на рис. 2.3.
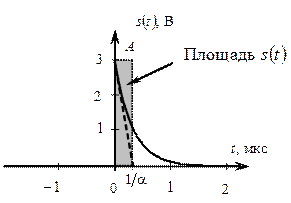
Рис. 2.3. Аналоговый импульсный сигнал s (t)
Спектр сигнала s (t) может быть найден путём подстановки выражения сигнала в формулу прямого преобразования Фурье:
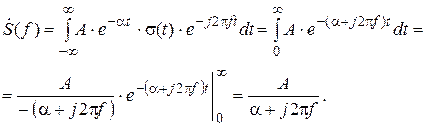
Действительная и мнимая части спектра сигнала s (t) показаны на рис.2.4, а АС и ФС – на рис. 2.5.
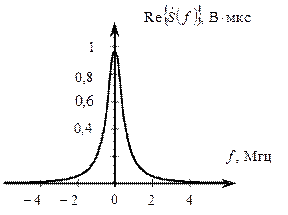
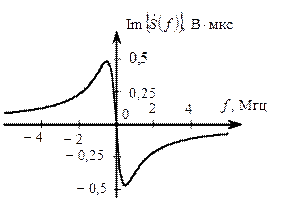
Рис. 2.4. Действительная и мнимая части спектра сигнала s (t)
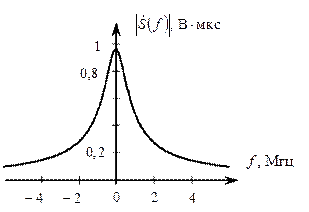
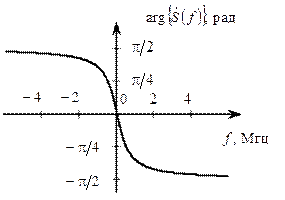
Рис. 2.5. Амплитудный и фазовый спектры сигнала s (t)
Из графиков видно, что действительная часть спектра и спектр амплитуд являются чётными функциями, а мнимая часть спектра и фазовый спектр – нечётными функциями, что подтверждает свойства симметрии спектров действительных сигналов.
Проверить правильность нахождения спектра сигнала можно с помощью свойства площади преобразования Фурье (свойство 17, прил. 2):
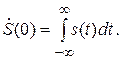
Площадь под экспоненциальной функцией может быть найдена как произведение А·(1/α). Таким образом, для сигнала s (t) получаем
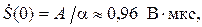
что совпадает со значением амплитудного спектра сигнала в нуле.
Пример 2.2
Найдём основные характеристики и параметры аналогового импульсного сигнала s (t), показанного на рис. 2.6. Параметры сигнала: А = 2 В, α = 3,14 1/мкс, τ0= 0,5 мкс.
Из рис. 2.6 видно, что аналитическое выражение сигнала s (t) может быть получено в виде суммы двух усеченных экспонент, одна из которых инвертирована во времени:

где сигнал s 1(t) определяется выражением
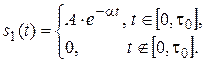
Сигнал s 1(t) можно выразить с помощью математических операций над односторонними экспонентами (рис. 2.7):
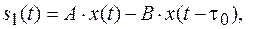
где 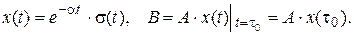
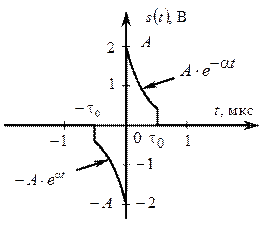
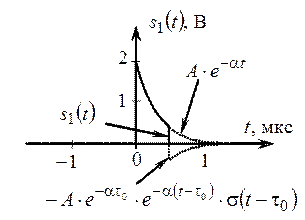
Рис. 2.6. Импульсный сигнал s (t) Рис. 2.7. Формирование сигнала s 1(t)
Получим временную функцию искомого сигнала s (t):
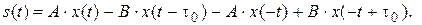
Теперь по известному спектру экспоненциального сигнала с использованием свойств линейности спектров и инвертирования сигнала во времени

где «*» означает комплексное сопряжение, можно найти спектр сигнала 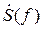 :
:

Полученное выражение позволяет оценить особенности спектра сигнала s (t). Спектр 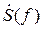 является чисто мнимым, что соответствует свойству спектров для нечетных временных функций. Мнимая часть спектра сигнала s (t) показана на рис. 2.8, амплитудный и фазовый спектры сигнала показаны на рис. 2.9.
является чисто мнимым, что соответствует свойству спектров для нечетных временных функций. Мнимая часть спектра сигнала s (t) показана на рис. 2.8, амплитудный и фазовый спектры сигнала показаны на рис. 2.9.
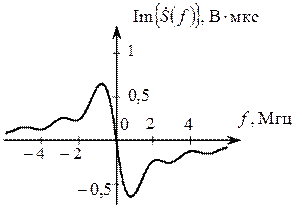
Рис. 2.8. Мнимая часть спектра импульсного аналогового сигнала s (t)
С помощью свойства площади преобразования Фурье (прил.2, свойство17) можно проверить правильность нахождения спектра сигнала:



Рис. 2.9. Амплитудный и фазовый спектры сигнала s (t)
Для определения эффективной ширины спектра сигнала найдём его энергию
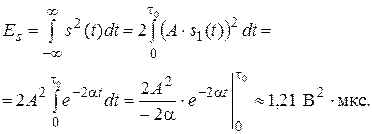
На рис. 2.10 показана зависимость части энергии сигнала в полосе F э от ширины интервала частот.
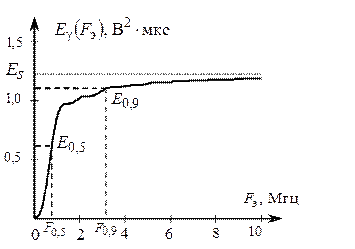
Рис. 2.10. Зависимость части энергии сигнала от ширины
интервала частот
Из рис. 2.10 видно, что 50% энергии сигнала сконцентрировано в полосе от нуля до F 0,5 = 0,77 МГц, а 90% энергии сигнала находится в полосе частот от нуля до F 0,9 = 3,25 МГц.
Пример 2.3
С помощью теорем о свойствах преобразования Фурье найти и проанализировать спектр аналогового трапецеидального сигнала s (t), изображенного на рис. 2.11 с амплитудой А и длительностью τ0.
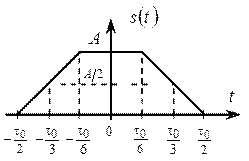
Рис. 2.11. Трапецеидальный сигнал
Аналитическое выражение сигнала s (t) имеет следующий вид:
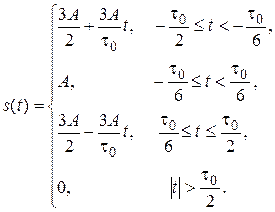
Вывод аналитического выражения для спектра сигнала 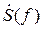 непосредственно прямым преобразованием Фурье (1.2) приведёт к громоздким преобразованиям и вызовет большие трудности. Воспользуемся тем, что трапецеидальный сигнал s (t) можно представить в виде свёртки двух прямоугольных импульсов s 1(t) и s 2(t), изображённых на рис. 2.12:
непосредственно прямым преобразованием Фурье (1.2) приведёт к громоздким преобразованиям и вызовет большие трудности. Воспользуемся тем, что трапецеидальный сигнал s (t) можно представить в виде свёртки двух прямоугольных импульсов s 1(t) и s 2(t), изображённых на рис. 2.12:
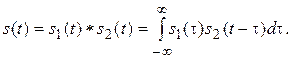
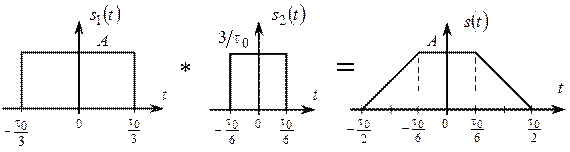
Рис. 2.12. Получение трапецеидального сигнала
Прямоугольный импульс s 1(t) имеет длительность 2 τ0/3, соответствующую длительности исходного трапецеидального сигнала по уровню 0,5 относительно амплитудного значения А. Прямоугольный импульс s 2(t) имеет длительность τ0/3 и амплитуду 3/τ0, т.е. является импульсом с единичной площадью.
Графическое проведение свёртки иллюстрируется рис. 2.13. На верхнем графике представлен первый сомножитель s 1(τ) подынтегрального выражения, следующий график показывает второй сомножитель s 2(t – τ) в зависимости от временного сдвига t. Отметим, что для t > 0 график второго сомножителя смещается вправо. Результат произведения двух сомножителей показан на третьем графике. Площадь под этим третьим графиком является результатом свёртки двух импульсов для конкретного временного сдвига t.

Рис. 2.13. Свёртка двух прямоугольных сигналов
Зависимость площади от временного сдвига t показана на нижнем графике рис. 2.13. Это и есть заданный трапецеидальный сигнал. Интересно отметить, что зависимость площади произведения на третьем графике совпадает с аналитическим выражением заданного сигнала для соответствующего интервала 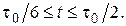
Искомый спектр определяется по теореме о спектре свёртки сигналов:
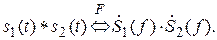
Прямоугольный импульс длительностью Т можно записать с использованием специальной функции:
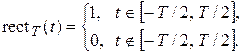
Спектр прямоугольного импульса амплитудой А и длительностью Т определяется следующим соотношением:
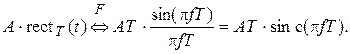
Используя выражения для спектров прямоугольных импульсов, получим спектральную функцию сигнала s (t):
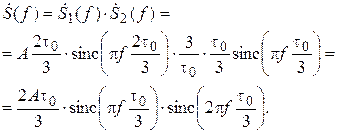
Спектр трапецеидального сигнала (рис. 2.11) является чётной действительной функцией, получаемой произведением спектров соответствующих прямоугольных сигналов. Спектры этих сигналов изображены на рис. 2.14 пунктирными линиями. Ширина главного лепестка амплитудного спектра составляет F, а уровень первого бокового лепестка составляет 0,086 от максимума.
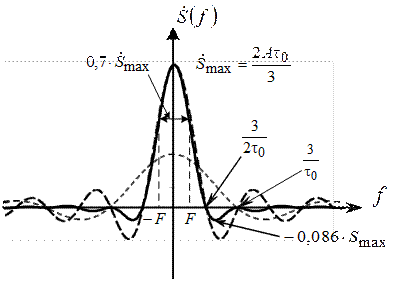
Рис. 2.14. Получение спектра трапецеидального сигнала
Значительно более наглядно эти параметры выглядят на графике амплитудного спектра, представленного в логарифмическом масштабе на рис. 2.15. Для сравнения пунктиром показан амплитудный спектр прямоугольного импульса с длительностью, равной длительности трапецеидального импульса по уровню 0,5 от амплитудного значения. Видно, что форма главных лепестков спектров этих сигналов практически одинакова, т.е. они имеют примерно одинаковую ширину спектра. Однако уровень первого бокового лепестка спектра трапецеидального сигнала на 8 дБ ниже уровня бокового лепестка прямоугольного сигнала.

Рис. 2.15. Амплитудный спектр в логарифмическом масштабе
Интересно отметить, что максимальное значение спектра сигнала 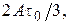 совпадает с площадью исходного трапецеидального сигнала. Это универсальное свойство спектров можно использовать, в частности, для проверки правильности нахождения спектра сигнала.
совпадает с площадью исходного трапецеидального сигнала. Это универсальное свойство спектров можно использовать, в частности, для проверки правильности нахождения спектра сигнала.
Пример 2.4
Рассмотрим пример нахождения характеристик аналогового импульсного сигнала (рис. 2.16), заданного выражением
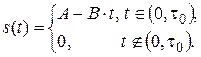
Параметры сигнала: А = 1 В, В = 0,5 В/мкс, τ0 = 2 мкс.
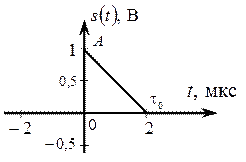
Рис. 2.16. Аналоговый импульсный сигнал s (t)
Для определения аналитического выражения спектра сигнала s (t) воспользуемся свойствами преобразования Фурье. Поскольку в таблице прил. 1 нет сигналов, похожих на заданный сигнал s (t), попробуем получить типовые сигналы с помощью математических операций над ним.
Продифференцируем сигнал s (t) по времени

де δ(t) – дельта-функция; 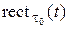 – прямоугольный импульс длительностью τ0, определяемый следующим соотношением:
– прямоугольный импульс длительностью τ0, определяемый следующим соотношением:

График функции сигнала s '(t) показан на рис. 2.17.
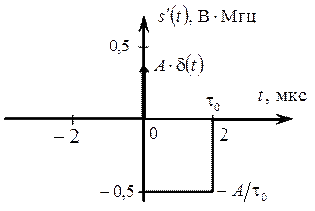
Рис. 2.17. Первая производная сигнала s (t) по времени
Спектры каждой из компонент сигнала s '(t) приведены в таблице прил. 1, поэтому можно записать
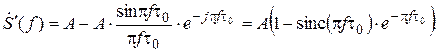
Для нахождения аналитического выражения спектра сигнала s (t) воспользуемся свойством интегрирования:
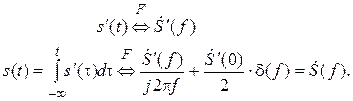
Поскольку в данном случае 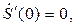 получаем
получаем
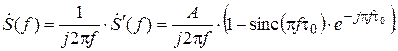
На рис. 2.18 представлены действительная и мнимая части спектра сигнала, а на рис. 2.19 – амплитудный и фазовый спектры сигнала s (t).
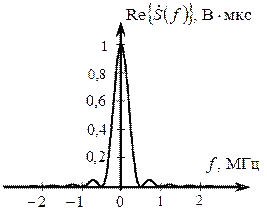
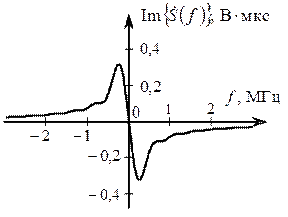
Рис. 2.18. Действительная и мнимая части спектра сигнала s (t)
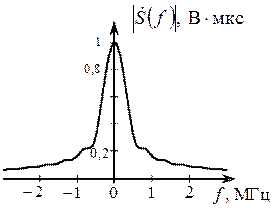
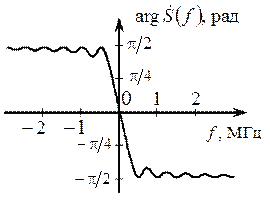
Рис. 2.19. Амплитудный и фазовый спектры сигнала s (t)
Проанализируем полученный спектр  . Модуль спектра (АС) представляет собой произведение двух функций: гиперболы A /2π f, вызванной скачком напряжения на величину А (рис 2.16), и спектра
. Модуль спектра (АС) представляет собой произведение двух функций: гиперболы A /2π f, вызванной скачком напряжения на величину А (рис 2.16), и спектра  , представленных на рис. 2.20. Результат произведения этих двух функций показан на рис. 2.21.
, представленных на рис. 2.20. Результат произведения этих двух функций показан на рис. 2.21.
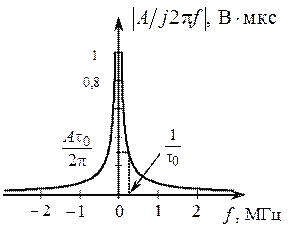
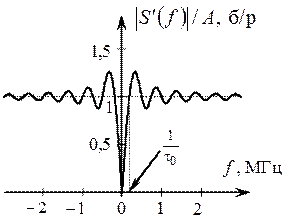
Рис. 2.20. Составляющие амплитудного спектра: 
аналогового импульсного сигнала s (t)
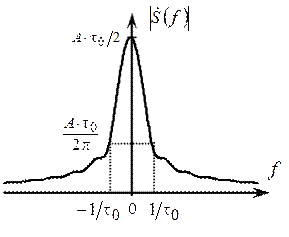
Рис. 2.21. Амплитудный спектр сигнала s (t)
В амплитудном спектре сигнала s (t) максимальное значение S (0) может быть определено по свойству площади преобразования Фурье как площадь исходного треугольного импульса:
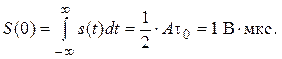
Ширина спектра и пульсации амплитудного спектра вокруг гиперболы определяются длительностью треугольного сигнала τ0. Определим энергию сигнала s (t). Для упрощения расчетов учтём, что энергия сигнала не зависит от положения сигнала на оси времени и от его инверсии по времени, поэтому расположим сигнал так, как показано на рис. 2.22.
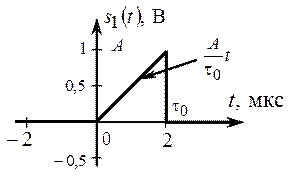
Рис. 2.22. Треугольный импульс, полученный из исходного сигнала s (t)
Энергия сигнала s (t) равна энергии сигнала s 1(t) и определяется следующим образом:
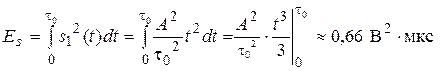
Энергетический спектр сигнала s (t) может быть определён следующим образом:
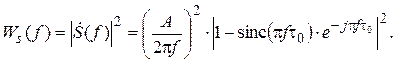
Энергетический спектр сигнала s (t) показан на рис. 2.23.
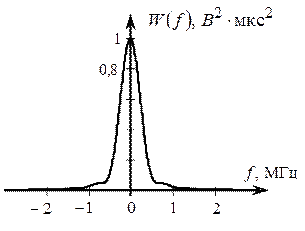
Рис. 2.23. Энергетический спектр сигнала s (t)
Определим энергетическую ширину полосы частот сигнала s (t) по графику, показанному на рис. 2.24.
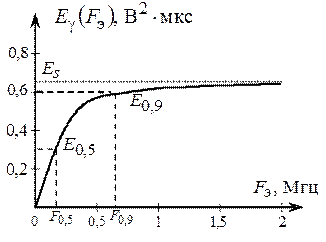
Рис. 2.24. Зависимость части энергии сигнала от полосы частот
Для восстановления сигнала по его спектру в эффективной полосе частот воспользуемся формулой обратного преобразования Фурье (1.19):

На рис. 1.26 показаны сигналы, восстановленные из спектра 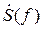 в полосе частот, в которой сконцентрировано 50% и 90 % энергии сигнала s (t). Из рис. 2.25 видно, что сигнал, восстановленный по 50% энергии не похож на исходный треугольный импульс, в то время как восстановление сигнала по 90% энергии привело к значительному уменьшению ошибки восстановления.
в полосе частот, в которой сконцентрировано 50% и 90 % энергии сигнала s (t). Из рис. 2.25 видно, что сигнал, восстановленный по 50% энергии не похож на исходный треугольный импульс, в то время как восстановление сигнала по 90% энергии привело к значительному уменьшению ошибки восстановления.
Увеличение параметра γ, т.е. расширение полосы частот F э приводит к уменьшению энергии разностного сигнала E ∆ Особого внимания заслуживает то, как восстанавливается скачкообразное изменение исходного сигнала.
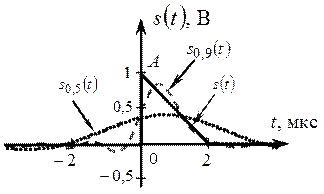
Рис. 2.25. Сравнение аналогового импульсного сигнала s (t)
с сигналами, восстановленными по разным полосам частот
Во-первых, все восстановленные сигналы проходят через середину скачка. Во-вторых, отклонение восстановленного сигнала от исходного имеет максимальную величину вблизи скачка. Максимальное отклонение определяется величиной скачка А и составляет примерно 12% от величины скачка. Такое поведение восстановленного сигнала вблизи скачка носит название эффекта Гиббса. В-третьих, период колебаний в восстановленном сигнале уменьшается с ростом эффективной полосы F э. И, наконец, скорость спада амплитуды колебаний увеличивается с ростом F э, что и объясняет в конечном итоге уменьшение энергии разностного сигнала при увеличении F э.
Пример 2.5
С помощью теорем о свойствах преобразования Фурье найдём аналитическое выражение спектра сигнала
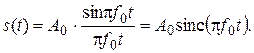
для А 0 = 2 В, f 0 = 2 МГц и построим графики амплитудного и фазового спектров.
Из графика функции сигнала s (t), показанного на рис. 2.26, видно, что форма сигнала с точностью до постоянных коэффициентов совпадает с формой спектра прямоугольного импульса (прил. 1). Это означает, что спектр сигнала s (t) может быть найден с помощью свойства дуальности частоты и времени (прил. 2):

где А, В – амплитудные коэффициенты; α и β – масштабные коэффициенты.
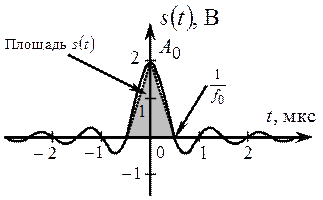
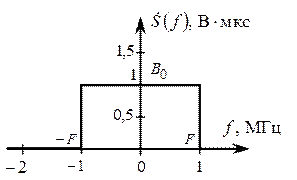
Рис. 2.26. Сигнал s (t). Рис. 2.27. Спектр сигнала s (t).
Таким образом, спектр заданного сигнала s (t) имеет форму прямоугольника на оси частот с неизвестными параметрами высоты В 0 и граничной частоты F, представленного на рис 2.27:

Коэффициент В 0 найдём исходя из свойства площади сигнала. Площадь под функцией вида sinc(x) равна площади треугольника, вписанного в главный лепесток функции:

Граничную частоту F можно определить по свойству площади спектра:
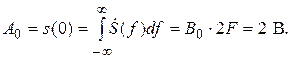
Отсюда получим F = f 0/2 = 1 МГц. Спектр сигнала s (t) является действительной чётной функцией.
|
|
|
|
|
Дата добавления: 2014-12-10; Просмотров: 6671; Нарушение авторских прав?; Мы поможем в написании вашей работы!