Уравнение состояния. Равновесное и неравновесное состояние термодинамической системы

Равновесное и неравновесное состояние термодинамической системы.

Если все термодинамические параметры состояния постоянны во времени и одинаковы во всех точках системы, то такое состояние системы называется равновесным. Если между различными точками в системе существуют градиенты температур, давлений и т. п., то она является неравновесной. В такой системе под действием градиентов параметров возникают потоки теплоты, вещества и т. п., стремящиеся вернуть ее в состояние равновесия. Опыт показывает, что изолированная система с течением времени всегда приходит в состояние равновесия и никогда самопроизвольно выйти из него не может.

В классической термодинамике рассматриваются только равновесные системы.

Для равновесной термодинамической системы существует функциональная связь между параметрами состояния, которая называется уравнением состояния.

Опыт показывает, что объем v, температура Т и давление р простейших систем, которыми являются газы и пары, связаны термическим уравнением состояния вида:

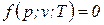, (1.16).

Существование этой зависимости между основными параметрами обусловлено тем, что величина каждого из них определяется положением и скоростями движения молекул, которые для каждого состояния имеют вполне определенные значения.

Уравнению состояния можно придать другую форму:

; ;

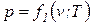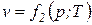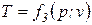
Эти уравнения показывают, что из трех основных параметров, определяющих состояние системы, независимыми являются два любых. Термодинамическое состояние газа можно считать известным, если заданы значения двух его параметров, т.к. третий параметр можно вычислить из уравнения состояния.

Дата добавления: 2014-11-29