Внутренняя энергия. Для некругового процесса равенство (I, 1) не соблюдается, так как система не возвращается в исходное состояние

Для некругового процесса равенство (I, 1) не соблюдается, так как система не возвращается в исходное состояние. Вместо этого равенства для некругового процесса можно записать (опуская коэффициент k):

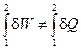
Так как пределы интегрирования в общем случае произвольны, то и для элементарных величин d W и d Q:

d Q ¹ d W,

следовательно:

d Q – d W ¹ 0

Обозначим разность d Q – d W для любого элементарного термодинамического процесса через dU:

dU º d Q – d W (I, 2)

или для конечного процесса:

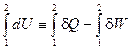(I, 3)

Возвращаясь к круговому процессу, получаем (из уравнения I, 1):

(I, 4)

Таким образом, величина dU является полным дифференциалом некоторой функции состояния системы. При возвращении системы к исходному состоянию (после циклического изменения) величина этой функции приобретает первоначальное значение.

Функция состояния системы U, определяемая равенствами (I, 2) или (I, 3), называется внутренней энергией системы.

Очевидно, выражение (I, 3) может быть записано следующим образом:

=U₂–U₁=∆U= (I, 5)

или:

U₂ – U₁ = ∆U = Q – W

Данное рассуждение обосновывает опытным путём наличие определенной функции состояния системы, имеющей смысл суммарной меры всех движений, которыми обладает система.

Иначе говоря, внутренняя энергия включает поступательную и вращательную энергию молекул, колебательную энергию атомов и групп атомов в молекулах, энергию движения электронов, внутриядерную и другие виды энергии, т. е. совокупность всех видов энергии частиц в системе за исключением потенциальной и кинетической энергии самой системы.

Предположим, что циклический процесс удалось провести так, что после того, как система вернулась к исходному состоянию, внутренняя энергия системы не приняла начального значения, а увеличилась. В этом случае повторение круговых процессов вызвало бы накопление энергии в системе. Создалась бы возможность превращения этой энергии в работу и получения таким путём работы не за счёт теплоты, а «из ничего», так как в круговом процессе работа и теплота эквивалентны друг другу, что показано прямыми опытами.

Невозможность осуществления указанного цикла построения вечного двигателя (перпетуум мобиле) первого рода, дающего работу без затраты эквивалентного количества другого вида энергии, доказана отрицательным результатом тысячелетнего опыта человечества. Этот результат приводит к тому же выводу, который в частной, но более строгой форме мы получили, анализируя опыты Джоуля.

Сформулируем ещё раз полученный результат. Полный запас энергии системы (её внутренняя энергия) в результате циклического процесса возвращается к исходному значению, т. е. внутренняя энергия системы, находящейся в данном состоянии, имеет одно определенное значение и не зависит от того, каким изменениям система подвергалась перед тем, как прийти к данному состоянию.

Иными словами, внутренняя энергия системы есть однозначная, непрерывная и конечная функция состояния системы.

Изменение внутренней энергии системы определяется выражением (I, 5); для кругового процесса справедливо выражение (I, 4). При бесконечно малом изменении некоторых свойств (параметров) системы внутренняя энергия системы изменяется также бесконечно мало. Это — свойство непрерывной функции.

В пределах термодинамики нет необходимости использовать общее определение понятия внутренней энергии. Формальное количественное определение через выражения (I, 2) или (I, 3) достаточно для всех дальнейших термодинамических рассуждений и выводов.

Поскольку внутренняя энергия системы есть функция её состояния, то, как уже было сказано, прирост внутренней энергии при бесконечно малых изменениях параметров состояний системы есть полный дифференциал функции состояния. Разбивая интеграл в уравнении (I, 3) на два интеграла по участкам пути от состояния 1 до состояния 2 (путь «а») (см. рис.2) и обратно — от состояния 2 до состояния 1 (иной путь «b» ), — получаем:

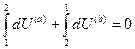(I, 6)

или

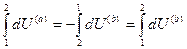(I, 7)

К тому же результату мы придем, сравнивая пути «а»и«с»или «b»и «с» и т. д.

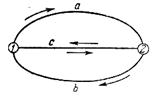
Рис. 2. Схема кругового (циклического) процесса.

Выражение (I, 7) показывает, что приращение внутренней энергии системы при переходе её из одного состояния в другое не зависит от пути процесса, а зависит только от начального и конечного состояний системы.

Дата добавления: 2014-11-29