Работа различных процессов

Под названием работы объединяются многие энергетические процессы; общим свойством этих процессов является затрата энергии системы на преодоление силы, действующей извне. К таким процессам относится, например, перемещение масс в потенциальном поле. Если движение происходит против градиента силы, то система затрачивает энергию в форме работы; величина работы положительна. При движении по градиенту силы система получает энергию в форме работы извне; величина работы отрицательна. Такова работа поднятия известной массы в поле тяготения. Элементарная работа в этом случае:

d W = – mgdH

где m — масса тела; H — высота над начальным нулевым уровнем. При расширении системы, на которую действует внешнее давление P, система совершает работу 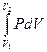, элементарная работа равна в этом случае PdV (V₁ и V₂ — начальный и конечный объёмы системы соответственно).

При движении электрического заряда q в электрическом поле против направления падения потенциала j и на участке, где изменение потенциала равно dj, а также при увеличении заряда тела, имеющего потенциал j, на величину dq работа совершается над системой, величина её равна в первом случае — qd j, а во втором случае — j dq.

Аналогичным образом можно выразить работу увеличения поверхности раздела S между однородными частями системы (фазами): d W = –s dS, где s — поверхностное натяжение.

В общем случае элементарная работа d W является суммой нескольких качественно различных элементарных работ:

d W = Pd V – mgdH – s dS – j d q + … (1, 11)

Здесь P, –mg, –σ, – j — силы в обобщённом смысле (обобщённые силы) или факторы интенсивности; V, H, S, q — обобщённые координаты или факторы ёмкости.

В каждом конкретном случае следует определить, какие виды работы возможны в исследуемой системе, и, составив соответствующие выражения для d W, использовать их в уравнении (I, 3). Интегрирование уравнения (I, 11) и подсчет работы для конкретного процесса возможны только в тех случаях, когда процесс равновесен и известно уравнение состояния.

Для очень многих систем можно ограничить ряд уравнения (I, 11) одним членом — работой расширения.

Работа расширения при равновесных процессах в зависимости от их особенностей выражается различными уравнениями, вытекающими из уравнения состояния. Приведем некоторые из них:

1) Процесс, протекающий при постоянном объёме (изохорный процесс; V = const):

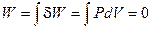(I, 12)

2) Процесс, протекающий при постоянном давлении (изобарный процесс; P = const):

W = 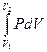= P(V₂ – V₁) = P D V (I, 13)

3) Процесс, протекающий при постоянной температуре (изотермический процесс, T = const). Работа расширения идеального газа, для которого PV = nRT:

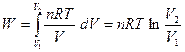(I, 14)

Отметим одно существенное обстоятельство. Расширение газа — неравновесный процесс, он протекает с конечной скоростью. В результате в объеме газа возникает турбулентность. При этом давление в отдельных частях системы оказывается различным и перестает быть параметром, определяющим её состояние. Следовательно, в общем случае применение предложенных уравнений для вычисления работы процесса расширения оказывается некорректным.

Тем не менее, указанный процесс может быть осуществлен бесконечно медленно через непрерывный ряд состояний, бесконечно близких к равновесным состояниям, причем не только в прямом, но и обратном направлении.

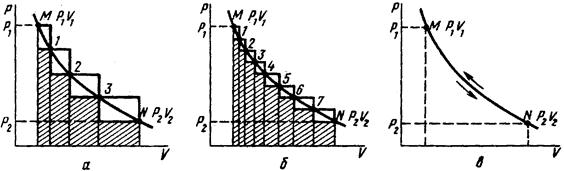
Рис.3. График процесса расширения и сжатия газа при неравновесных (а, б) и равновесных (квазистатических) (в) условиях.

Рассмотрим расширение газа в цилиндре с подвижным поршнем. Допустим, что поршень нагружен гирьками с одинаковым весом (внешнее давление). Точкой М (рис.3а) представим исходное равновесное состояние системы. После снятия одной гирьки давление и объём газа в системе скачкообразно изменятся. Новое равновесное состояние, в которое придет система после снятия первого груза, обозначим точкой 1. После снятия второго груза давление и объём опять изменятся и система снова перейдет в состояние равновесия (точка 2). Допустим, что данная операция повторяется четыре раза, тогда изменения давления и объёма системы изобразятся нижней ломаной линией MN, где точка N — конечное равновесное состояние системы. Площадь между нижней ломаной линией MN и осью абсцисс будет равна совершенной (полученной) работе в процессе расширения газа.

Теперь проведем обратный процесс — будем постепенно нагружать поршень гирьками и тем самым сжимать газ. Процесс сжатия газа изобразится верхней ломаной линией MN (рис.3а). Площадь между ней и осью абсцисс будет равна работе, затраченной на сжатие газа. Из рисунка следует, что полученная работа меньше затраченной работы. Их разность равна площади, заключенной между верхней и нижней ломаными линиями.

Проведем процесс расширения и сжатия газа в цилиндре по-иному: величину каждого груза уменьшим, например, вдвое, а общее внешнее давление оставим неизменным.

Полученная работа, как это следует из рисунка 3б, при этом увеличится, а затраченная на сжатие газа работа, наоборот, уменьшится. Уменьшится и разность между этими работами.

Из рассмотренных здесь двух процессов расширения и последующего сжатия газа вытекает: если внешнее давление изменится на бесконечно малую величину dP, то ломаные линии прямого и обратного процессов практически совпадут с кривой MN (рис.3в). Полученная работа при расширении газа будет максимальной, а затраченная работа при сжатии газа будет минимальной. Их разность будет стремиться к нулю. Число точек на линии MN, отвечающих промежуточным состояниям равновесия, будет бесконечно большим. Следовательно, процесс сжатия и расширения газа в последнем случае окажется бесконечно медленным и будет непрерывно проходить через состояния, бесконечно близкие к равновесным, что отвечает определению равновесного (квазистатического) процесса.

Внешнее давление при квазистатическом процессе на бесконечно малую величину dP отличается от внутреннего давления в системе, которое может быть вычислено из уравнения состояния, например, для идеального газа — из уравнения состояния Менделеева‑Клапейрона.

Дата добавления: 2014-11-29