Адиабатические процессы в газах

Говорят, что термодинамическая система совершает адиабатический процесс, если он обратим и если система термически изолирована, так что во время процесса не происходит теплообмена между системой и окружающей средой.

Если дать возможность газу адиабатически расширяться, то он произведёт работу и её величина будет положительной.

Так как газ термически изолирован (Q = 0), то значение ∆U должно быть отрицательным, т. е. во время адиабатического расширения внутренняя энергия газа уменьшается.

Из уравнения (I, 43) следует:

PdV + C_VdT = 0 (I, 45)

Выразив давление из (I, 39) и разделив на T, получим

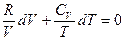
Полагая C_V независимым от T и интегрируя, получаем:

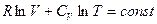
Из (I, 41) следует, что R = C_P – C_V. Подставляя это выражение для R и деля на C_V получаем:

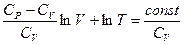
Если ввести обозначение 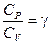, то после потенцирования получим уравнение адиабаты:

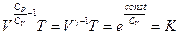, (I, 46)

где K и 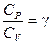— постоянные. Величина 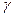называется показателем адиабаты.

Подстановка 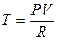и 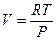приводит к двум другим возможным формам уравнения адиабаты:

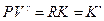(I, 47)

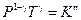(I, 48)

Уравнения (I, 46), (I, 47) и (I, 48) являются термодинамическими уравнениями, т. к. они вытекают из первого закона термодинамики и уравнения состояния идеального газа, поэтому применимы лишь к идеальным газам и не являются общими уравнениями, справедливыми для любых систем.

Уравнение (I, 47) следует сравнить с уравнением изотермы для идеального газа:

PV = const

На диаграмме P – V изотермы являются семейством равнобочных гипербол. Адиабата (кривая 1 – 3 (рис.4)) по сравнению с гиперболой (кривая 1 – 2) круче, т. к. показатель степени g больше единицы.

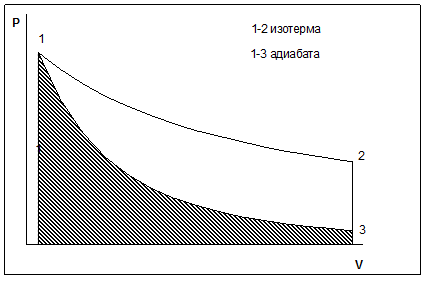
Рис. 4. Работа, совершаемая при адиабатическом расширении идеального газа.

Когда идеальный газ расширяется адиабатически от состояния 1 до состояния 3, кинетическая энергия его молекул, следовательно, и температура газа уменьшаются. Работа, которая производится во время расширения, равна, очевидно, заштрихованной области на рис.4. Она, как уже отмечалось выше, будет положительной

Интересным и простым приложением теории адиабатического расширения газов является вычисление изменения температуры при удалении от земной поверхности. Основной причиной изменения температуры являются конвекционные токи в тропосфере, которые непрерывно перемещают воздух из нижних слоёв в более высокие слои и наоборот. Когда воздух с уровня моря поднимается в верхние слои с низким давлением, он расширяется. Т. к. воздух — плохой проводник тепла, то теплота от окружающего воздуха очень мало передаётся новым подвижным слоям, поэтому можно считать, что происходит адиабатическое расширение. Соответственно понижается температура поднявшегося воздуха. С другой стороны, воздух верхних слоёв атмосферы, опускаясь вниз, испытывает адиабатическое сжатие, вследствие чего повышается температура.

Чтобы рассчитать изменение температуры, рассмотрим столб воздуха с единичным сечением. Гидростатическое давление столба воздуха высотой dH равно rg dH, где g — ускорение свободного падения, а r — плотность воздуха.

Следовательно, при подъёме на расстояние dH давление уменьшится на величину .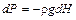

Из уравнения Менделеева-Клапейрона 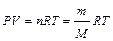получаем:

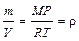, где m — масса и М — молекулярная масса газа. Тогда

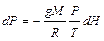(I, 49)

После логарифмирования и дифференцирования уравнения (I, 48) получаем:

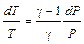(I, 50)

Подставляя в (I, 50) значение dP из (I, 49), получаем:

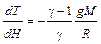
Полагая R = 8,314 , g = 9,81 , M = 0,0289 и

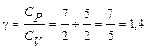(газы земной атмосферы двухатомны, ничтожными количествами одноатомных инертных газов можно пренебречь), получим:

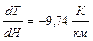
В действительности эта величина несколько больше, чем наблюдаемое среднее снижение температуры в зависимости от высоты над уровнем моря. Разница объясняется главным образом тем, что мы пренебрегли эффектом конденсации водяного пара в расширяющихся массах воздуха.

Рассмотренные ранее отдельные типы процессов (изохорный, изобарный, изотермический и адиабатный) являются частными предельными случаями реальных процессов. Соответствующие им теплоемкости также являются частными видами теплоемкости. Реальные процессы в газах часто протекают по путям, промежуточным между указанными. Эти процессы носят общее название политропных процессов или политроп и могут приближенно характеризоваться значением показателя политропы n в уравнении политропы. Для идеального газа оно имеет следующий вид:

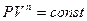
Дата добавления: 2014-11-29