
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основные аффинные задачи
|
|
|
|
Основные аффинные и метрические задачи
Задача называется метрической, если в ней фигурируют метрические свойства фигур, т.е. свойства, которые можно выявить непосредственным измерением (длина отрезка, расстояние между точками, расстояние от точки до прямой или плоскости, величина угла, перпендикулярность, площадь, объем). В аффинных задачах метрические свойства не рассматриваются. Аффинные задачи решаются в аффинной системе координат, а, следовательно, и в прямоугольной декартовой. Метрические задачи удобно решать в прямоугольной системе координат.
Основные аффинные и метрические задачи, решаемые с помощью координат, сформулируем в виде теорем.
1. Координаты вектора, заданного двумя точками.
Теорема 1. Если в аффинной системе координат 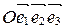
 и
и 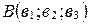 , то
, то 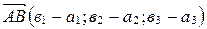 .
.
 Представим вектор
Представим вектор 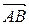 в виде разности векторов
в виде разности векторов 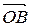 и
и 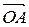 :
:
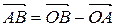 .
.
 Так как
Так как  , то по определению координат точки
, то по определению координат точки 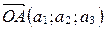 . Аналогично
. Аналогично 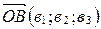 . Применяя свойство координат векторов (координаты разности двух векторов равны разности их соответствующих координат), получаем, что вектор
. Применяя свойство координат векторов (координаты разности двух векторов равны разности их соответствующих координат), получаем, что вектор  имеет координаты
имеет координаты 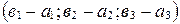 Þ
Þ 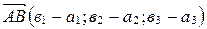 .
.
2. Деление отрезка в данном отношении.
Говорят, что точка М делит направленный отрезок  в отношении
в отношении 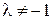 , если выполняется векторное равенство:
, если выполняется векторное равенство:
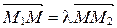 . (1)
. (1)
Число 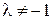 при этом называется простым отношением трех точек М1, М2 и М. Простое отношение трех точек М1, М2 и М обозначается так:
при этом называется простым отношением трех точек М1, М2 и М. Простое отношение трех точек М1, М2 и М обозначается так: 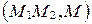 .
.
Почему в определении деления отрезка в данном отношении 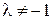 ?
?
Пусть М1 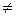 М2 и точка М делит направленный отрезок
М2 и точка М делит направленный отрезок  в отношении l=-1. Тогда по определению деления отрезка в данном отношении
в отношении l=-1. Тогда по определению деления отрезка в данном отношении
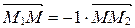 ,
,
т.е.  Þ
Þ 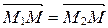 Þ
Þ  . А так как начало у векторов
. А так как начало у векторов 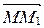 и
и 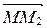 общее и они равны, то М1=М2. Получили противоречие с условием, следовательно,
общее и они равны, то М1=М2. Получили противоречие с условием, следовательно, 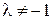 .
.
Из векторного равенства (1) следует, что если  , то
, то 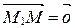 , т.е. точка М совпадает с точкой М1; если l>0, то точка М лежит внутри отрезка
, т.е. точка М совпадает с точкой М1; если l>0, то точка М лежит внутри отрезка 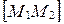 (рис. 37), т.е.
(рис. 37), т.е.  ; если l<0, то точка М лежит на прямой
; если l<0, то точка М лежит на прямой 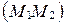 вне отрезка
вне отрезка 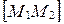 (рис. 38), т.е.
(рис. 38), т.е. 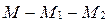 или
или 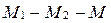 .
.
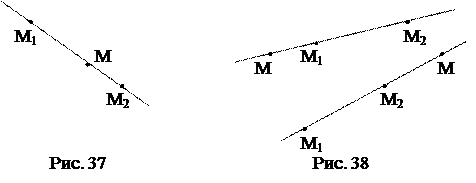
Теорема 2. Пусть в аффинной системе координат 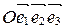
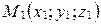 ,
, 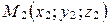 . Тогда координаты точки
. Тогда координаты точки 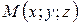 , делящей направленный отрезок
, делящей направленный отрезок  в отношении
в отношении 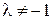 , находятся по формулам:
, находятся по формулам:
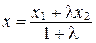 ;
; 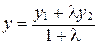 ;
; 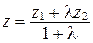 . (2)
. (2)
 По определению деления отрезка в данном отношении
По определению деления отрезка в данном отношении 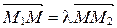 .
.
 По теореме 1
По теореме 1 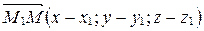 ,
, 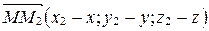 . Тогда
. Тогда 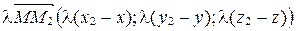 . Так как два вектора равны тогда и только тогда, когда равны их соответствующие координаты, то
. Так как два вектора равны тогда и только тогда, когда равны их соответствующие координаты, то 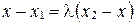 ;
; 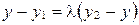 ;
; 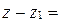

 , откуда получаем:
, откуда получаем: 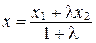 ;
; 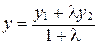 ;
; 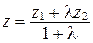 .
.
Формулы (2) называются формулами деления отрезка в данном отношении в координатах.
Из теоремы 2 получаем
Следствие. Если М(х;у;z) – середина отрезка М1М2 с концами 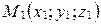 и
и 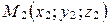 , то
, то 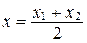 ,
, 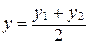 ,
, 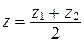 .
.
 Так как М – середина М1М2, то
Так как М – середина М1М2, то 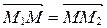 Þ l=1. Применяя формулы деления отрезка в данном отношении в координатах, получаем:
Þ l=1. Применяя формулы деления отрезка в данном отношении в координатах, получаем:

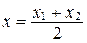 ,
, 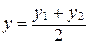 ,
, 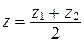 .
.
Основная метрическая задача
Теорема 3(расстояние между двумя точками в координатах). Если в прямоугольной декартовой системе координат 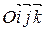
 ,
, 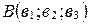 , то расстояние АВ между точками А и В находится по формуле:
, то расстояние АВ между точками А и В находится по формуле:
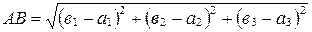 .
.
 Учитывая, что
Учитывая, что  ,
, 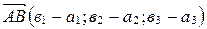 и используя формулы для нахождения длины вектора в координатах, получаем:
и используя формулы для нахождения длины вектора в координатах, получаем:

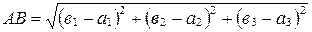 .
.
Формулы, доказанные в теоремах 1 и 2, можно использовать и в аффинной, и в прямоугольной декартовой системе координат, а формулу из теоремы 3 – только в прямоугольной декартовой системе координат.
Задания для самостоятельной работы
1. Найдите координаты точки А, если В (3;0;-2), 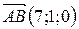 .
.
2. С – середина отрезка АВ. Найдите координаты точки В, если А (1;0;-4), С (3;1;0).
3. Точки Р и Q лежат внутри отрезка АВ, причем АР=РQ=QВ. Найдите (ВQ,А).
4. На плоскости дан отрезок [АВ]. Постройте точку С, делящую направленный отрезок 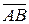 в отношении
в отношении 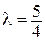 ;
; 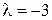 .
.
5. Известны координаты вершин треугольника АВС: А(4;3), В(0;5),С(-2;2). Пользуясь теоремой, обратной теореме Пифагора, выясните, будет ли этот треугольник прямоугольным.
6. Можно ли вывести формулы для нахождения расстояния между двумя точками, координаты которых даны в аффинной системе координат?
|
|
|
|
|
Дата добавления: 2014-12-10; Просмотров: 3786; Нарушение авторских прав?; Мы поможем в написании вашей работы!