Исключающее ИЛИ

Логическое сложение (операция ИЛИ, дизъюнкция)

Логическое сложение двух переменных X₁ и X₂ есть логическая функция Y, которая истинна тогда, когда истинна хотя бы одна входная переменная.

Таблица истинности для логического сложения имеет вид:

X1	X2	Y

В символах алгебры логики операция И записывается следующим образом:

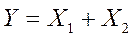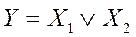или

Логическая операция, результат которой для двух переменных Х1 и Х2 является истиной при разных значениях этих переменных.

Таблица истинности для этой операции имеет вид:

X1	X2	Y

Рассмотренные функции позволяют реализовать любую логическую зависимость. В реализации современных логических схем широкое распространение получили логические функции ИЛИ-НЕ, И-НЕ. На их основе строятся цифровые устройства, входящие в состав вычислительных машин. Работа таких устройств описывается некоторой логической функцией, представляющей собой сравнительно сложное логическое выражение. Для практической реализации это выражение минимизируют с использованием правил алгебры логики. Наиболее распространенные правила:

1. Логическое произведение любого аргумента на 0 всегда равно 0:

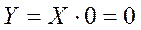
2. Логическое произведение любого аргумента на 1 равно значению аргумента:

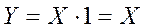
3. Логическое произведение одних и тех же аргументов равно значению аргумента:

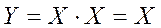4.Логическое произведение аргумента и его инверсии равно нулю:

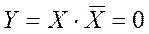
5.Логическое сложение аргумента с 0 равно значению аргумента:

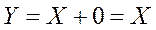6.Логическое сложение аргумента с единицей равно единице:

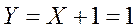7. Логическое сложение одних и тех же аргументов равно значению аргумента:

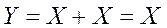
8. Логическое сложение аргумента с его инверсией равно единице:

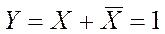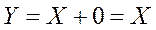
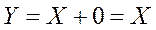
9.Двойная инверсия аргумента равна значению аргумента

10. Переместительный закон:

11.Сочетательный закон:

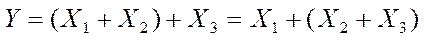12. Распределительный закон:

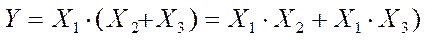
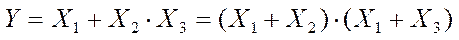13. Закон поглощения:

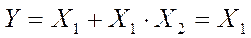14. Закон склеивания:

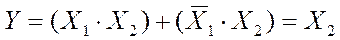
Правила алгебры логики применяют для преобразования исходных выражений к виду, удобному для их практической реализации. Используя эти правила, можно спроектировать практически любой цифровой автомат.

Вопросы для самоконтроля

1. Системы счисления, применяемые в компьютерах.

2. Как перевести десятичное число в двоичное?

3. Как перевести десятичное число в шестнадцатеричное?

4. Как перевести двоичное число в шестнадцатеричное?

5. Как перевести двоичное число в десятичное?

6. Как перевести десятичную дробь в двоичное число?

7. Как обрабатываются в компьютере отрицательные числа?

8. Какие основные математические операции выполняет компьютер?

9. Что такое «таблица истинности»?

10. В чем смысл логической операции отрицания?

11. В чем заключается операция логического сложения?

12. В чем заключается операция логического умножения?

Тесты

1. В компьютере могут использоваться системы счисления:

+двоичная

+ двоично-десятичная

+ шестнадцатеричная

- восьмеричная

2.Способ наименования и изображения чисел с помощью символов, имеющих определенные количественные значения

+ система счисления

- кодирование

- программирование

- представление

3.Десятичное число 248 в шестнадцатеричной системе счисления имеет значение

- E7

+ F8

- 96

- 6D

4. Десятичное число 384 в двоичной системе счисления имеет значение

-110011001

[phone]

- 101101100

- 100011011

5. Двоичное число 11011001 в десятичной системе счисления имеет значение

- 354

+217

- 237

- 321

6. Двоичное число 11011001 в шестнадцатеричной системе счисления имеет значение

- FE

+D9

- F9

- E8

7. Используя девятиразрядные двоичные числа можно записать _ целых чисел

- 361

+ 512

- 496

- 464

8. В процессе обработки число 10010011 инвертируется, а затем представляется в шестнадцатеричной форме и будет иметь вид:

- 93

+6С

- D3

- DE

9. После упрощения выражения получается

+Х₁

- Х₁+Х₂

- Х₂

- Х₁Х₂

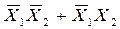10. После упрощения выражения получается

-

+

-

-

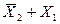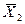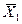РАЗДЕЛ 2. технические средства РЕАЛИЗАЦИИ информаЦИОННЫХ ПРОЦЕССОВ

Дата добавления: 2014-12-10