Найдите производные следующих функций

Решите следующие задачи самостоятельно.

12.1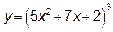

12.2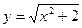

12.3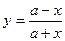

12.4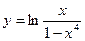

12.5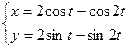

ЗАДАНИЕ №13

Найти пределы функции, применяя правило Лопиталя.

Для раскрытия неопределённостей вида 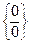или 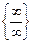используется правило Лопиталя:

Пусть 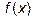и 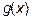две дифференцируемые на некотором интервале функции, причем 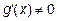, и пусть пр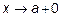и (или 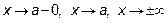), обе эти функции стремятся к нулю (или 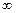). Тогда, если 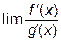при данном стремлении x существует, то существует и

.

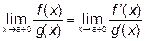Пример 1. Найти предел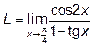

Решение: При 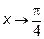имеем неопределённость 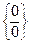. Функции 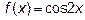, , 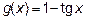дифференцируемы в некоторой окрестности точки 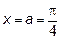, причем 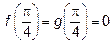. Если 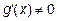, то по правилу Лопиталя получим:

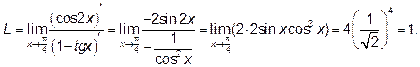
Ответ: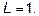

Если отношение производных опять представляет собой неопределенность, вида 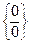или 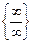, то можно снова применить правило Лопиталя, т.е. перейти к отношению вторых производных и т.д.

Пример 2. Найти предел .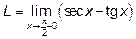

Решение: При 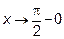получается неопределенность вида 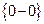. Выполняя преобразования, указанную неопределённость приведем к виду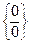

Теперь при 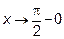и числитель, и знаменатель стремятся к нулю. Применяем правило Лопиталя

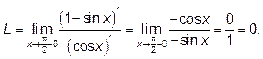
Ответ: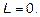

Встречаются также неопределенности типа 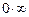. Они раскрываются аналогично предыдущему случаю, то есть приводятся к виду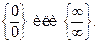

Пример 3. Найти предел .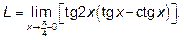

Решение: Здесь 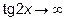, 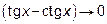при 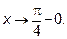. Следовательно имеем неопределенность 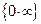. Приводим эту последовательность к виду 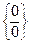и получаем

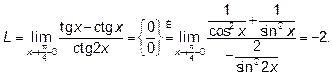
где буква Л над знаком равенства означает применение правила Лопиталя.

Ответ: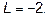

Подробнее о вычислении пределов по правилу Лопиталя можно прочесть в [1] гл.4 §2, 4, 5 и найти соответствующие задачи в [3].

Следующие задачи решите самостоятельно:

13.1 Вычислить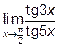

13.2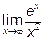

13.3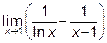

ЗАДАНИЕ №14

Следующая задача посвящена исследованию графика функции методами дифференциального исчисления.

Подробно об этом можно прочесть в [1], гл.11, [4] гл.5.

I. Методами дифференциального исчисления исследовать функцию 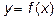для 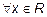и по результатам исследования построить ее график.

II. Найти наименьшее и наибольшее значения функции на отрезке[a;b].

I. Для исследования функции используется общая схема исследования функции.

1. Найти область допустимых значений (ОДЗ) аргумента функции .
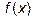2. Найти точки пересечения функции 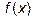с осями координат Оx и Oy.
3. Найти точки разрыва и определить тип.
4. Установить, является ли функция 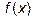четной, нечетной и периодической.
5. Найти асимптоты графика функции .
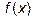6. Найти 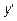, определить точки экстремумов 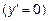и интервалы возрастания 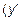>0) и убывания 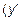<0) графика функции .
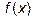7. Найти 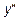, определить точки перегиба ( 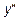=0) и интервалы выпуклости ( 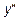<0) и вогнутости ( 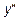>0) графика функции .
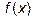8. По результатам исследования построить график функции .

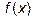II. План нахождения наибольшего и наименьшего значений функции 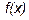на отрезке [a,b].

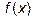
1. Найти критические точки функции 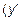=0 или не существует).
2. В каждой критической точке определить знак производной 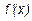слева и справа. Если 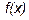меняет знак при переходе через критическую точку, то в данной точке функция 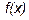имеет локальный экстремум, иначе эта точка не является точкой экстремума.
3. Вычислить значения функции 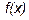в точках экстремума и при x=a, x=b.
4. Среди этих значений найти наибольшее и наименьшее значения функции 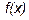на отрезке [a,b].

Пример 1. Пусть .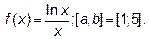

Решение:

1. Функция 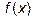определена и непрерывна в интервале 0<x<+∞, т.к. область допустимых значений для функции y=lnx: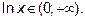
2. В точке 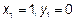график 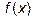пересекает ось Ox. С осью Oy график функции 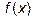не пересекается.
3. В граничной точке x=0 области допустимых значений функция 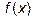имеет бесконечный разрыв II рода, потому что

.

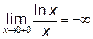1. Функция 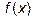является четной, нечетной или периодической, если выполняется одно из равенств 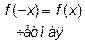, , 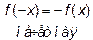, 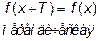где T>0 –период.

Заданная функция не является четной или нечетной, т.к. для x <0 она не определена.

Находим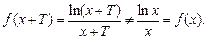

Следовательно, 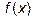является функцией общего вида.

1. Так как в точке x=0 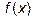имеет бесконечный разрыв, то прямая x=0 (ось Oy) является вертикальной асимптотой.

Ищем наклонные асимптоты .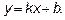

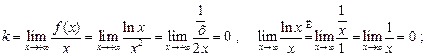
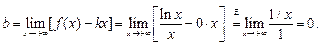
Поэтому 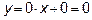(ось Ox) есть горизонтальная асимптота (y=0)

1. Находим 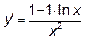и критические точки:

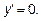
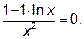1-lnx=0. lnx=1. x=e.

Исследуем знак производной в каждом из интервалов (O,e) и (e,∞), на которые критическая точка разбивает область определения функции.

Возьмем точку в (O,e), например, 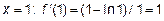>0; возьмем точку в (e,∞), например,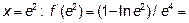 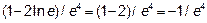<0.

Составим таблицу

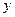
	(0,e)	e≈2.72	(e,+∞)
	+		-
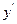
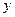
	Возрастает		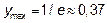Убывает

1. Находим вторую производную , , , , , .

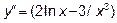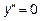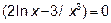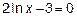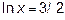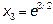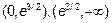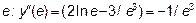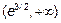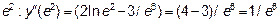Определяем знак второй производной на интервалах . Возьмем в интервале точку <0. Возьмем в интервале точку >0.

Составим таблицу

	-		+
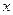
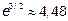
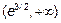
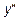
График	Выпуклый		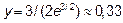Вогнутый

Точка перегиба имеет координаты .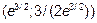

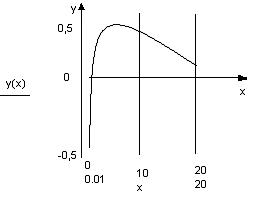
1. На основании полученных данных строим график. По оси Ox удобно взять масштаб, равный 1, а по оси Oy, равный 0.1.

На отрезке [1; 5] функция имеет локальный максимум в точке 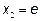, равный 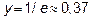. Вычисляем значения функции 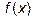в точке x=1 и x=5: y(1)=0, .

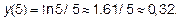Следовательно, на отрезке [1; 5] .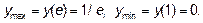

Решите самостоятельно следующие задачи:

14.1. Определите интервалы возрастания и убывания функции .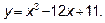

14.2. Найти экстремум функции 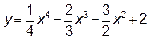и определить ее наибольшее и наименьшее значение на отрезке [-2,4].

14.3. Найти асимптоты графика функции .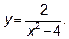

14.4. Найти асимптоты кривой .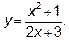

14.5. Исследовать функцию .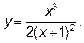

Задачи на эту тему можно найти в [3] гл.7 §2.

ЗАДАНИЕ №15

Далее в контрольных работах любой специальности следует задача на интегрирование. Подробнее о неопределенных интегралах можно прочесть в [4] гл.10 и в[1] гл XII

Функция f(x) является первообразной для функции f(x ) на промежутке x, если

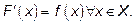
Совокупность всех первообразных называется неопределённым интегралом от функции f(x)

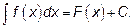
где С – произвольная постоянная

Свойства неопределенного интеграла.

1. Если a – постоянная величина, то 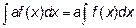, т.е. постоянный множитель можно выносить за знак интеграла.

2. Интеграл от алгебраической суммы конечного числа функций равен такой же алгебраической сумме интегралов от слагаемых функций

.

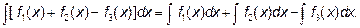3. 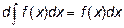, т.е. знак дифференциала d и знак интеграла 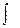взаимно уничтожаются в указанном порядке.

4. 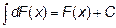знаки d и 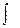взаимно погашаются и в таком порядке, лишь следует добавить произвольную константу.

Основная таблица интегралов.

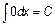
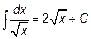
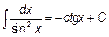
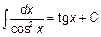
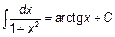
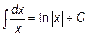
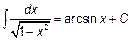
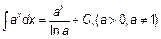
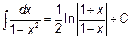
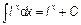
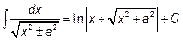
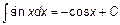
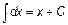
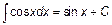
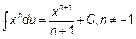
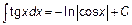
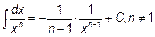
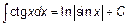
Непосредственное интегрирование.

Пример 1. Найти .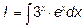

В простейших примерах применяется метод непосредственного интегрирования, то есть используются свойства и таблицы интегралов. А именно, при помощи тождественных преобразований подынтегрального выражения исходный интеграл сводится к табличному интегралу или к сумме табличных интегралов.

Решение: Положим

a=3e

на основании свойств показательной функции и по таблице интегралов получаем:

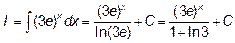
Интегрирование по частям.

Пример 2. Найти интеграл: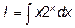

Решение: Используем метод интегрирования по частям, основанный на следующем свойстве интегралов:

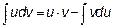
Очевидно, что применять эту формулу имеет смысл только в том случае, если интеграл в правой части проще, чем в левой, например:

1. Если подынтегральное выражение слева содержит сомножитель

arcsin x, arcos x, arctg x, ln x

то в качестве u(x) выбирают эти функции.

2. Если подынтегральная функция имеет вид

,

где 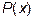- многочлен степени “n”.

Тогда в качестве u(x) берут P(x) и интегрируют по частям n раз. В нашем примере подынтегральное выражение имеет вид

,

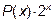Где 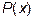- многочлен первой степени х.

Итак, мы должны взять

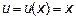
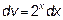
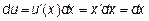
При промежуточном интегрировании постоянную С опускаем.

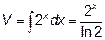
Затем отыскиваем интеграл в правой части при

и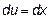

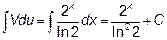
По интегрированию по частям получаем:

.

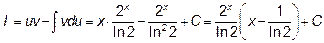Замена переменной под знаком интеграла.

Пример 3. Найти: А) ;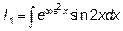

Б) .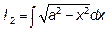

Решение: Воспользуемся методом замены переменной. Если

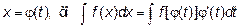
Здесь мы заменили переменную х выражением через t, а dx на .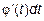

а) Найдем 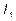. Для этого обозначим 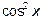через t, тогда

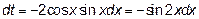
Видим что выражение справа – это часть подынтегрального выражения, то есть

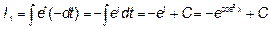
Это пример основан на выделении дифференциала новой переменной. Такой вариант метода замены переменной называют «подведением» под знак дифференциала, то есть при

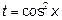
подынтегральная функция является функцией промежуточной переменной умноженной на дифференциал этой переменной:

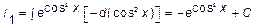
Иногда удобнее действовать иначе. В случае:

б) имеем иррациональную подынтегральную функцию. Чтобы избавиться от этой иррациональности, воспользуемся основным тригонометрическим тождеством. Для того, чтобы перейти к тригонометрическому виду сделаем замену переменной. Положим

.

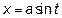Стало быть

.

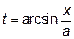Тогда

.

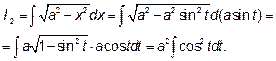Для того чтобы избавиться от степени тригонометрической функции, перейдем к двойному углу.

Имеем

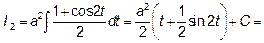
Перейдем обратно к переменной х

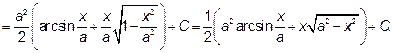
Интегрирование рациональной функции.

Пример 4. Найти: А) ,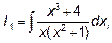

Б)

Решение: Как в примере А), так и в примере Б) подынтегральная функция является рациональной дробью, то есть дробью вида

,

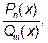где P и Q многочлены степени соответственно m и n.

А) Степени числителя и знаменателя совпадают и равны 3. В этом случае, поделив числитель на знаменатель как многочлен на многочлен, получим сумму многочлена и остатка деления – правильной рациональной дроби. Интегрирование многочленов не сложно, а правильная рациональная дробь раскладывается на сумму дробей стандартного вида – так называемых «простейших» дробей, то есть дробей вида

.

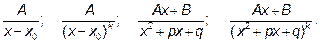Интегралы от этих дробей известны. Итак, разделим числитель подынтегрального выражения на знаменатель как многочлен на многочлен.

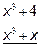
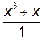
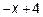
Таким образом, в результате деления мы получим частное, равное 1 и остаток равный (-х + 4). Итак, неправильную дробь можно разложить следующим образом

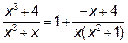, то есть

в виде суммы многочлена нулевой степени и правильной дроби. Теперь правильную дробь надо разложить на простейшие. У нас знаменатель уже разложен на множители

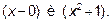
Так бывает не всегда. Если это не так, его надо разложить на множители и в соответствии с ними разложить вашу правильную дробь на сумму простейших дробей методом неопределенных коэффициентов:

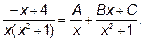
Приведя к общему знаменателю, получаем:

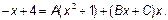
Два многочлена равны, если равны коэффициенты при соответствующих степенях неизвестного. Приравнивая коэффициенты при одинаковых степенях многочлена в левой части и многочлена в правой, получим:

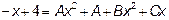
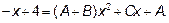
Приравняв коэффициенты при

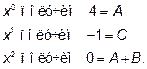
Решив совместно эти уравнения, получим

А = 4, В = -4, С = -1

Итак 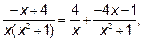, а

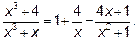
Следовательно,

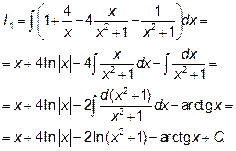
Заметим, что если 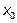- действительный корень знаменателя кратности k, то в разложении ему будут соответствовать k простейших дробей вида 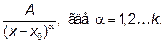. В нашем примере многочлен, стоявший в знаменателе рациональной дроби, имеет один действительный корень 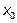= 0 кратности единица – следовательно, в разложении рациональной дроби на сумму простейших этому корню соответствует одно слагаемое.

Если знаменатель имеет комплексные корни, то только попарно сопряженные, так как коэффициенты знаменателя вещественны. Пусть знаменатель кратности 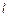имеет комплексно сопряженные корни 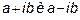кратности 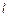. Тогда в разложении на простейшие дроби им будут соответствовать 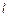простейших дробей вида

,

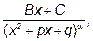где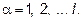

В нашем примере такие комплексные корни имел двучлен 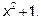. Действительно, приравняв его к нулю, получим 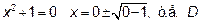<0 – а это означает, что действительных корней нет, 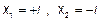комплексно сопряжённые корни кратности 1.

Б) Найдем 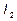. Не всегда следует стремиться сразу, определить правильность дроби и разлагать ее на простейшие. В этом задании рациональную дробь можно проинтегрировать без привлечения этого метода.

Подынтегральное выражение равно 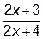. Конечно, можно воспользоваться тем, что это неправильная рациональная дробь и проинтегрировать ее, разлагая на сумму многочлена и простейших дробей. Однако, если сделать замену переменой 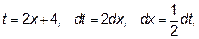, получим:

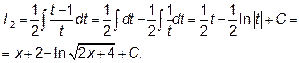
В каждом примере на интегрирование результат можно проверить. Достаточно продифференцировать ответ. Если интегрирование было верно, то получится подынтегральное выражение.

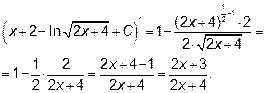
Мы получили подынтегральную функцию.

Пример 5. Найти интегралы: А)

Б)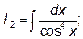

В)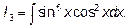

Решение: В данном примере найти требуется интегралы от тригонометрических функций. Интегралы вида

,

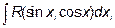где R – рациональная функция от 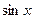и 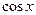сводятся к интегралу от рациональной функции относительно новой переменной интегрирования с помощью универсальной тригонометрической подстановки 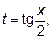, тогда

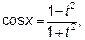
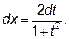
В случае А) универсальная тригонометрическая подстановка дает

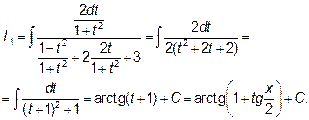
Но часто универсальная подстановка приводит к громоздким выкладкам, поэтому, где удается, применяют другие подстановки

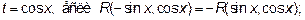
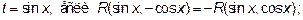
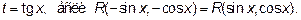
Случай Б) как раз относится к третьему типу, а именно подынтегральная функция четна как относительно 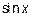, так и относительно 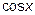. Положив 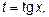получим 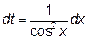и 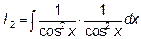и заменив 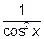по известной тригонометрической формуле

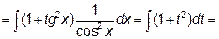
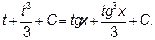
Случай В) относится к первому типу, а именно подынтегральная функция нечетна относительно синуса. Положив 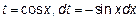и заменив 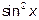на 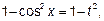, получим

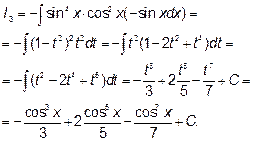
Задачи на эту тему можно найти в [3] гл.9

Дата добавления: 2014-12-10