Рассмотрим пример

Вычислить приближенное значение определенного интеграла 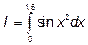с помощью формулы Симпсона, положив n=4.

Формула Симпсона приближенного интегрирования позволяет численно определить значение интеграла без нахождения первообразной. Для этого достаточно вычислить значение функции в n=4 точках, полученных в результате разбиения отрезка 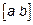на n отрезков (n – четное число) 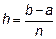шаг разбиения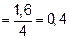 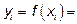значение подынтегральной функции на концах отрезков.

Составим таблицу:

K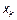
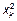
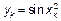
		0,00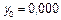
	0,4	0,16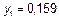
	0,8	0,64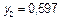
	1,2	1,44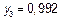
	1,6	2,56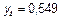

Формула Симпсона

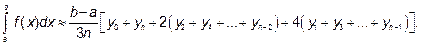
Подставив в эту формулу конкретные значения, получим

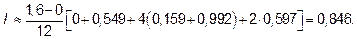
Вычислять интегралы приближённо можно не только при помощи метода Симпсона, но и других методов. Подробнее об этих методах можно прочитать в[1] гл. XIII,[4] гл.11 пр.8

Решите самостоятельно задачу:

18.1 Найдите число 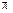, пользуясь интегралом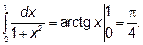

ЗАДАНИЕ №19

Все следующие задачи будут относиться к функциям нескольких переменных. Переменные x,y,z,t… называются независимыми между собой, если каждая из них может принимать любые значения в своей области изменения, независимо от того, какие значения принимают при этом остальные переменные. Переменная величина U называется функцией независимых переменных, если каждой совокупности значений этих переменных в области их изменения соответствует единственное определённое значение и: u=f(x,y,z,…t)

Областью определения функции f(x,y…t) называется совокупность значений независимых переменных x,y…t, при которых функция определена.

Частные приращения функции

Если u=f(x,y,z) и одна из независимых переменных, например x, получила приращение 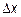, то частным приращением 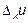функции называется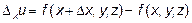

Аналогично для y и для z или любой другой переменной в случае большего числа переменных.

Частные производные

Составим отношение 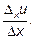Если при стремлении 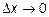это отношение стремится к определённому пределу, то этот предел называется частной производной функции U по независимой переменной X обозначается 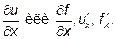Таким образом 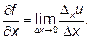Аналогично 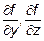и т.д.

Вычисление частных производных функции нескольких независимых переменных производится по тем же правилам, по которым вычисляются производные функции одной независимой переменной, следует лишь считать постоянными все независимые переменные, кроме той, по которой вычисляется частная производная.

Пример 1 Дана функция двух переменных 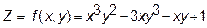. Найти все частные производные первого и второго порядков.

Решение: Частные производные от функции нескольких переменных по одной из переменных находятся в предположении, что другие переменные являются постоянными величинами. Таким образом, функция нескольких переменных становится обычной функцией одной переменной, к которой применяются все известные правила дифференцирования функции одной переменной.

Требуется найти 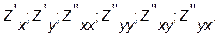Положим

Находим производную функции 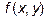по переменной :

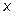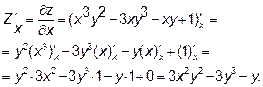
Полагая 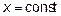, находим первую производную функции

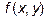по переменной y:

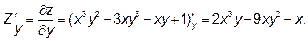
Теперь найдем производные второго порядка. Возьмем первую производную по 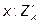, считая 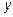постоянным, продифференцируем еще раз по .

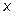Получим 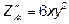. Если, считая x постоянным, мы продифференцируем 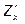ещё раз, но уже по y, то получим

.

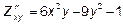Теперь возьмем первую производную по 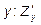и считая x постоянным, продифференцируем 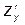еще раз по y. Мы получим

.

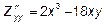Если мы, взяв 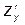, и считая y постоянным, продифференцируем 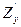еще раз, но по переменной x получим

.

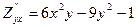Обратим внимание, что 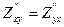; это равенство справедливо при условии непрерывности данных производных.

Подробнее о функциях нескольких переменных можно прочесть в [4] гл.8,[1] гл. XV и найти задачи в [3] гл.8.

Дата добавления: 2014-12-10