V. Оценочные средства

Курсовая работа по дисциплине «Эконометрика» не предусмотрена.

Примерные варианты письменных домашних заданий

Один из вариантов письменного домашнего задания №1.

Задача. Проводится анализ взаимосвязи количества населения Х (млн. чел.) и количества практикующих врачей Y (тыс. чел.) за десятилетний период:

год
Х	10.0	10.3	10.4	10.55	10.6	10.7	10.75	10.9	10.9	11.0
Y	12.1	12.6	13.0	13.8	14.9	16.0	18.0	20.0	21.0	22.0

Задание.

1. Постройте корреляционное поле и по его виду определите форму зависимости между Х и Y.

1. Оцените по МНК параметры уравнения линейной регрессии.
2. Оцените выборочный коэффициент корреляции и сделайте предварительный вывод о силе линейной взаимосвязи параметров Х и Y.
3. Проверьте качество уравнения регрессии:
1. значимость параметров регрессии;
2. интервальные оценки параметров регрессии;
3. значимость уравнения регрессии в целом;
4. интервальную оценку остаточной дисперсии.
4. Проинтерпретируйте результаты.
5. Сделайте прогноз среднего (индивидуального) значения количества практикующих врачей и постройте доверительный интервал для него при значении Х = Х_прогн..

Уровень значимости = 0,05; Х_прогн= 11.5 (млн. чел.).

Один из вариантов письменного домашнего задания №2.

Задача. Изучается влияние выработки продукции на одного работника (х₁ - единиц) и доли продукции, производимой на экспорт (х₂ - %) на величину прибыли (у - млн руб.) концерна. Для этого по 10 предприятиям концерна были получены данные приведенные в таблице. Построить регрессионную модель: у = β₀ + β ₁ х₁ + β ₂ х₂ + ε

i	хi1	хi2	yi	i	хi1	хi2	yi

Задание.

1. По МНК оценить коэффициенты линейной регрессии β_i, i =0, 1, 2 и записать выборочное уравнение регрессии.
2. Оценить статистическую значимость найденных параметров регрессии b _i, i =0, 1, 2.
3. В соответствие с заданным значением построить доверительные интервалы для найденных параметров;
4. В соответствие с заданным значением построить доверительный интервал для остаточной дисперсии;
5. Вычислить коэффициент детерминации R² и оценить его статистическую значимость при заданном значении ;
6. Определить какой процент разброса зависимой переменной объясняется данной регрессией;
7. Сравнить коэффициент детерминации R² со скорректированным коэффициентом детерминации;
8. Посредством коэффициентов b _i, i = 1, 2, влияние объясняющих переменных Х₁, Х₂ на изменение объясняемой переменной;
9. Спрогнозировать значение объясняемой переменной Y_прогн для прогнозных значений Х_{1 прогн}, Х_{2 прогн} и построить доверительный интервал для среднего (индивидуального) значения Y_прогн;

Х_{1 прогн} = 14 единиц, Х_{2 прогн} =8 %, = 0,01.

Один из вариантов письменного домашнего задания №3.

Задача. По этой теме используется задача, приведенная в письменном домашнем задании №1.

Задание.

1. По данным таблицы к линейной модели, полученной в письменном домашнем задании №1: а) применить тест ранговой корреляции Спирмена для оценки гетероскедастичности при 5% уровне значимости; б) применить тест Голдфелда-Квандта для оценки гетероскедастичности при 5% уровне значимости.

2. По данным таблицы рассчитать: а) параметры степенной функции у=β₀ 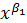*ε; б) параметры равносторонней гиперболы у=β₀+β₁/x+ε; в) параметры экспоненциальной функции у= 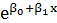*ε; г) параметры полулогарифмической функции у=β₀+β ₁lnx+ε; д) параметры обратной функции у=1/(β₀+β₁x+ε); е) параметры функции у=β₀+β₁ 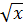+ε; ж) параметры показательной функции у=β₀ 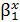*ε; з) оценить с надежностью 0.95 значимость полученных уравнений с использованием F-критерия.

3. По данным таблицы для временного ряда х_t: а) найти уравнение неслучайной составляющей (тренда), полагая тренд линейным; б) выявить на уровне значимости 0.05 наличие автокорреляции возмущений с использованием критерия Дарбина-Уотсона; в) найти с надежностью 0.95 интервальную оценку остаточной дисперсии , полагая тренд линейным; г) найти коэффициент автокорреляции (для лага τ=1,2,3); д) найти с надежностью 0.95 интервальную оценку коэффициента регрессии β₁, полагая тренд линейным; е) оценить с надежностью 0.95 значимость коэффициента парного регрессии с использованием t-критерия, полагая тренд линейным; ж) найти точечную и с надежностью 0.95 интервальную оценку прогноза среднего (индивидуального) значения количества населения на момент времени t=11 (одиннадцатый год), полагая тренд линейным; з) проверить с надежностью 0.95 значимость парной регрессии с использованием F-критерия, полагая тренд линейным.

Вопросы для подготовки к защите индивидуального задания:

1. Что такое функция регрессии?

2. Назовите основные причины наличия в регрессионной модели случайного отклонения.

3. Что понимается под спецификацией модели, и как она осуществляется?

4. В чем состоит различие между теоретическим и эмпирическим уравнениями регрессии?

5. В чем суть метода наименьших квадратов (МНК)?

6. Приведите формулы расчета коэффициентов эмпирического парного линейного уравнения регрессии по МНК.

7. Как связаны эмпирические коэффициенты линейной регрессии с выборочным коэффициентом корреляции?

8. Проинтерпретируйте коэффициенты эмпирического парного линейного уравнения регрессии.

9. Как определяются стандартные ошибки регрессии и коэффициентов регрессии?

10. Опишите схему проверки гипотез о величине коэффициентов регрессии.

11. В чем суть статистической значимости коэффициентов регрессии?

12. Приведите схему определения интервальных оценок коэффициентов регрессии.

13. Как строится и что позволяет определить доверительный интервал для условного математического ожидания зависимой переменной?

14. В чем суть предсказания индивидуальных значений зависимой переменной?

15. Объясните суть коэффициента детерминации.

16. В каких пределах изменяется коэффициент детерминации?

Дата добавления: 2014-12-10