Решение. Примеры решения задач

Примеры решения задач

1. Экономика страны описывается производственной функцией вида Y = A·K^0,4·L^0,6. Известно, что темп прироста капитала равен 3% в год, а численности занятых – 2%. Общая производительность факторов растет с темпом 1,5% в год. Как меняется объем производства?

В неоклассической модели роста была использована производственная функция вида Y = AF(K,L). Объем производства Y зависит от вклада факторов – труда L и капитала K, а также от технологии. Производственная функция имеет постоянную отдачу от масштаба, т. е. увеличение всех факторов в определенной степени приводит к росту выпуска в той же степени. Изменение выпуска можно представить как ДY = AF(K,L)·ДА + МРК·ДК + МРL·ДL, где МРК и МРL – предельные производительности соответствующих факторов.

Разделим это выражение на Y = AF(K,L) и получим: 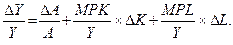Второе и третье слагаемое в правой части уравнения умножим и разделим на К и L: 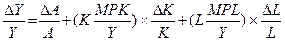. В скобках мы получим доли капитала и труда в общем объеме выпуска. При условии постоянной отдачи от масштаба сумма этих долей равна единице (по теореме Эйлера), тогда 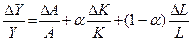, где б – доля капитала, а (1 – б) – доля труда в доходе, А – общая производительность факторов, мера уровня технологического прогресса, измеряемая обычно по остаточному принципу («остаток Солоу»).

В представленной функции Y = A·K^0,4·L^0,6 показатели степени представляют и долю факторов в доходе, то есть 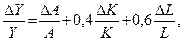что можно проверить математически, проведя с этой функцией все указанные выше операции.

Тогда то есть выпуск растет с темпом 3,9% в год.

2. Производственная функция задана уравнением 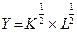. Норма сбережения s равна 0,2, норма выбытия d – 5%, тем роста населения n составляет 2% в год, темп трудосберегающего технологического прогресса g равен 3%. Каким будет запас капитала и объем выпуска в расчете на одного занятого в устойчивом состоянии? Соответствует ли устойчивая фондовооруженность уровню, при котором достигается максимальный объем потребления («золотому правилу»)? Какой должна быть норма сбережения в соответствии с «золотым правилом»?

Дата добавления: 2014-12-10