Модель сопряжения элементов 2 страница

Это общая задача линейного программирования – ограничения в виде неравенств (несбалансированная транспортная модель).

Модель, в которой ограничения имеют вид равенств, называется сбалансированной транспортной моделью.

Несбалансированная модель может быть приведена к сбалансированной – неравенства заменены равенствами (в общем случае путем введения фиктивных неотрицательных переменных – фиктивного поставщика или потребителя продукции).

Замкнутая транспортная модель предполагает ограничения в виде равенств:

- сумма спроса равна сумме предложений;

- спрос каждого пункта потребления удовлетворяется полностью;

- весь продукт из каждого пункта производства должен быть вывезен.

Особая структура замкнутой транспортной задачи (все ограничения имеют вид равенств) позволяют решать ее простыми методами.

На пересечении i -ой строки и j -го столбца стоит тариф с и сюда же заносится значение х _ij – количество продукции, поставляемой от i -го поставщика j -му потребителю.

При большой размерности задачи (m x n) отыскание оптимального плана путем непосредственного перебора становится трудоемкой. Решение транспортной задачи состоит из двух этапов: нахождение начального плана, улучшение его и получение оптимального плана перевозок.

К рассмотренной транспортной задаче приводятся различные практические задачи, никак не связанные с планированием перевозок, но которые могут быть сформулированы в терминах транспортной задачи.

Для решения транспортной задачи составляется транспортная таблица.

Номер поставщика	Номер потребителя	Предло-жение
		...	j	...	n
	c 11 x 11	c 12 x 12	...	c 1j x 1j	...	c 1n x 1n	a 1
	c 21 x 21	c 22 x 22	...	c 2j x 2j	...	c 2n x 2n	a 2
...	...	...	...	...	...	...	...
i	c i1 x i1	c i2 x i2	...	c ij x ij	...	c in x in	a i
...	...	...	...	...	...	...	...
m	c m1 x m1	c m2 x m2	...	c mj x mj	...	c mn x mn	a m
Спрос	b 1	b 2	...	b j	...	b n

В общем случае транспортную модель можно применять для описания ситуаций, связанных с управлением запасами, управлением движением капиталов, составлением расписаний, назначением персонала и др.

Хотя транспортная задача может быть решена как обычная задача линейного программирования, ее специальная структура позволяет разработать алгоритм с упрощенными вычислениями(на основе симплекс-метода).

Задача коммивояжера.

Пример простой комбинаторной задачи – задача о назначениях. Здесь требование целочисленности выполняется автоматически, поскольку задача о назначениях представляет собой частный случай транспортной задачи (в котором m = n, a _i = b _j = 1). Более общий случай представляет собой задача коммивояжера.

Имеется n +1 городов; задана матрица С = расстояний между этими городами. Выезжая из исходного города (с номером 0), коммивояжер должен побывать во всех остальных городах по одному разу и вернуться в город 0. В каком порядке объезжать следует города, чтобы суммарное расстояние было минимальным?

Это напоминает задачу о назначениях (минимизация суммарного расстояния), но уже не по всем матрицам перестановок, что усложняет решение.

Параметры задачи

x _ij = 1, если коммивояжер из города i переезжает в город j,

x _ij = 0 в противном случае,

где i, j = 0, 1, 2,..., n.

Задача минимизации

(суммарное расстояние минимальное)

при условиях

(коммивояжер выезжает из каждого города, кроме начального, один раз)

(коммивояжер въезжает в каждый город, кроме начального, один раз)

u_i – u_j + nх _ij ≤ n - 1, , i ≠ j.

Здесь переменные u_i принимают целые неотрицательные значения. Последнее условие вводится для того, чтобы путь коммивояжера не распался на несколько не связанных между собой подциклов (задача о назначениях) – любой путь состоит из одного цикла.

Задача о ранце.

Имеется n предметов, вес предмета j – a _j, его ценность – с _j. Требуется загрузить ранец набором предметов с общим весом А с максимальной суммарной ценностью.

Введем переменные x _j, , имеющие следующий смысл

x _j = 1, если j-й предмет подлежит загрузке,

x _j = 0 в противном случае.

Задача о ранце сводится к максимизации

с ₁ х ₁ + с ₂ х ₂ +.... + с _n x _n → max

при условиях

x _j = 1,

x _j = 0

а ₁ х ₁ + а ₂ х ₂ +.... + а _n x _n ≤ А.

Пример.

Оптимальная загрузка бомбардировщиков различных типов бомбовым запасом с целью максимизации суммарного эффекта данной системы боевых операций.

Обозначим через i = 1, 2,..., m типы бомб, через j = 1, 2,..., n – типы бомбардировщиков, через к = 1, 2,..., р – боевые операции.

Введем величины

bi- имеющийся запас бомб типа i,

aik- эффективность бомбы типа i на операции к,

nj- планируемое число вылетов бомбардировщика j,

wk- "вес", приписываемый командованием операции к.

Искомой величиной здесь является

xijk- количество бомб типа I, подлежащее загрузке в бомбардировщик j при его использовании в операции к.

Задача сводится к минимизации суммарного эффекта

при ограничениях

, i = 1, 2,..., m

x _ijk ≥ 0, x _ijk – целые числа.

Общая задача теории расписаний.

Обычно это задача календарного планирования, и ее варианты являются схемами основных задач по организации производства.

Имеется n станков и m деталей, каждая из которых должна пройти обработку на всех станках в определенной последовательности. Задано а _ij – время, необходимое для обработки j -ой детали на i -ом станке. Требуется найти такой порядок обработки деталей, который минимизировал бы общее время выполнения всех работ (длину производственного цикла). Несмотря на большое прикладное значение, пока получено решение только для случая двух станков. В этом случае, поскольку операции на первом станке можно выполнить без задержек, оптимизация заключается в минимизации суммарного времени простоя второго станка.

Примеры сведения практических задач к канонической транспортной задаче

Многие практические задачи, связанные с планированием перевозок, не укладываются в рамки рассмотренной задачи, так как осложнены дополнительными ограничениями.

Суммарный объем производства больше потребления - может быть введен фиктивный пункт потребления В_{n +1} с объемом потребления

b_{n +1 =} b_{n +1} – суммарный объем нереализованного продукта.

Размеры остатков в разных пунктах производства можно регулировать введением штрафа за единицу нереализованного продукта А _i.

Суммарный объем производства меньше потребления, то полное удовлетворение всех пунктов потребления невозможно. В этом случае необходимо организовать перевозки всего произведенного продукта так, чтобы наиболее важные пункты удовлетворялись полнее, и при этом суммарные транспортные расходы должны быть минимальны – вводится величина ущерба r _j при неудовлетворении пункта В _j.

Требуется минимизировать суммарные затраты

при условиях

, , x_ij > 0, y_j = b _j - , где

y_j – разность между потребностями пункта В _j и поставками в него.

Перевозки с резервированием.

В некоторых районах пунктов производства может возникнуть необходимость в резервировании определенного количества продукта.

I _к – совокупность номеров i -го пункта производства в к -ом районе.

Требуется организовать перевозки таким образом, чтобы в к -ом районе (к=1,…,s) сохранилось не менее V _к единиц продукта.

- V _к , .

Общее число продуктов, вывезенных из всех пунктов производства к -го района должно быть не менее, чем на V _к (величину заданного резерва) меньше суммарного количества продукта, произведенного в этом районе.

Задача сводится к задаче транспортного типа

При условиях

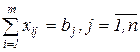- удовлетворение спроса каждого пункта потребления;

из каждого пункта потребления не может быть вывезено продукта

больше, чем производится;

- V _к , - условие резервирования;

x_ij ≥ 0 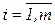, 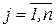- объем перевозок неотрицательные числа (перевозки запрещены из пунктов потребления в пункты производства).

Пришли к задаче планирования перевозок, обеспечивающего удовлетворение спроса всех пунктов потребления, и гарантирующего сохранение требуемых резервов в каждом районе.

Ограничения на пропускные способности магистралей (в ограниченный промежуток времени) не позволят реализовать оптимальный план перевозок, полученный без учета этих ограничений.

В этом случае в транспортной задаче условие xij ≥ 0 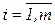, 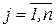заменяется неравенством вида 0 ≤ хij ≤ dij, где dij – пропускная способность магистрали (ij), т.е. максимальный объем продукции, который может быть перевезен по этой магистрали за рассматриваемый промежуток времени. Такая задача может быть вообще неразрешимой (когда пропускная способность всех магистралей, ведущих к j-му потребителю меньше объема его потребностей).

Перевозки с промежуточной обработкой.

Задача может быть осложнена наличием промежуточных транспортных узлов, в которых производится обработка груза (перевалка на другой вид транспорта, доработка полуфабриката перед поступлением его в пункт потребления).

А₁,…, А_m – пункты производства с объемами производства а₁, …, а_m

В₁,…, В_n – пункты потребления с объемами потребления b₁,…, b_n

С₁,…, С_к – пункты промежуточной обработки.

Возможности пункта промежуточной обработки С_λ ограничены d _λ единицами продукта.

Стоимости перевозки единицы полуфабриката продукта из А_i в С_λ составляет С_iλ‘, стоимость перевозки единицы полуфабриката продукта из С_λ в В_j составляет С_λj“.

Составить такой план перевозок, при котором весь полуфабрикат вывозится, полностью обрабатывается, потребности всех пунктов потребления удовлетворяются и при этом транспортные расходы минимальны.

Математическая модель.

Z_iλj – количество продукта, доставляемое из пункта А _i в В_j через С _λ.

Транспортная таблица.

	B 1	B 2	…	B n	B n+1	B n+2	…	B n+k-1	B n+k
А 1	M	M		M	c’ 11	c’ 12		c’ 1,k-1	c’ 1k	a 1
А 2	M	M		M	c’ 21	c’ 21		c’ 2,k-1	c’ 2k	a 2
...				…						…
А m	M	M		M	c’ m1	c’ m2		c’ m?k-1	c’ mk	a m
А m+1	c” 11	c” 12		c” 1n		M		M	M	d 1
А m+2	c” 21	c” 21		c” 2n	M			M	M	d 2
…										…
А m+k-1	c” k-1,1	c” k-1,2		c” k-1,n	M	M	…		M	d k-1
А m+k	c” k1	c” k2		c” kn	M	M		M		d k
	b 1	B 2	…	B n	d 1	d 2	…	d k-1	d k

Определить план перевозок { Z _iλj}, на котором достигается минимум линейной формы

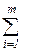
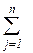(С _iλ‘ + С _λj“) Z _iλj → min

при условиях

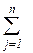Z _iλj = а _i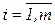

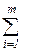
Z _iλj = b _j

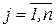
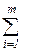
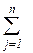Z _iλj ≤ d _λ

Z _iλj ≥ 0, , ,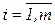

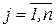
Необходимое и достаточное условие разрешимости задачи

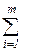а _i = b _j ≤ d _λ

Преобразуем, введя новые переменные

x _i,n+λ – количество полуфабриката, поступающее из пункта производства А _i в пункт обработки С _λ.

x _m+λ,j - количество полуфабриката, поступающее из пункта обработки С _λ в пункт потребления В_j.

x _i,n+λ = Z _iλj, , .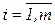

x _m+λ,j = Z _iλj, , .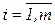

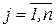В новых переменных задача формулируется так: требуется минимизировать

С _iλ‘ x _i,n+λ + 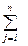С _λj“ x _m+λ,j

при условиях

x _i,n+λ = а _i, ,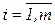

x _m+λ,j = b _j ,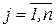

x _i,n+λ = x _m+λ,j ≤ d _λ

x _i,n+λ ≥ 0, x _m+λ,j ≥ 0, , , .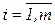

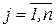6.3 Распределительные задачи линейного программирования

Задачи распределения применяются при планировании множества операций, требующих одни и те же ресурсы и одно и то же оборудование. Предполагается, что каждая операция может быть выполнена многими способами, но для выполнения каждой операции наиболее подходящим путем не хватает ресурсов и оборудования. Задача заключается в том, чтобы, используя ограниченные мощности и наличные материалы, выполнить все работы оптимальным образом.

Задачи распределения в общем виде можно разделить на два вида:

1. Задан объем работ. Имеются определенные ресурсы, т.е. фиксированные производственные мощности и количество материалов. Необходимо найти такой вариант использования ресурсов, который обеспечит минимальные затраты на выполнение заданных работ;

2. Заданы определенные материалы и оборудование (ресурсы). Необходимо определить, какая работа дает максимальную прибыль при использовании этих ресурсов.

Несмотря на требование линейности функций критериев и ограничений, в рамки линейного программирования попадают многочисленные задачи распределения ресурсов, управления запасами, сетевого и календарного планирования, транспортные задачи и прочие. Рассмотрим некоторые из них.

Дата добавления: 2014-11-29