Выбор средств доставки грузов

Распределение транспортных единиц по линиям

Имеется n транспортных линий, по j–ой линии необходимо выполнить bj рейсов 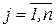. В наличии имеются транспортные единицы m типов. Резервы полезного времени транспортной единицы типа i составляют аi 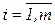. На выполнение транспортной единицей типа i рейса j требуется время tij, а затраты на рейс составляют сij. Требуется найти наиболее экономичную расстановку транспортных единиц по линиям.

Математическая модель

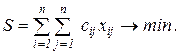(суммарные транспортные расходы минимальные)

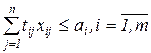(ограничения по фондам времени каждой транспортной единицы)

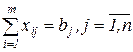(все рейсы должны быть выполнены)

хij ≥ 0, 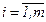, , 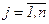хij – целые.

Имеется m грузообразующих пунктов с объемами грузов а_i 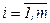. Имеется n средств доставки грузов (видов транспорта), грузоподъемность j –го средства доставки составляет р_j, а наличный его парк равен N_j, 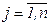. Грузы подлежат доставке в один центральный пункт (склад), затраты при осуществлении одной единицей средства доставки j–го рейса от пункта i до склада равны с _ij.

Через х_ij обозначим количество средств доставки типа j, отправляющееся из пункта i.

Математическая модель

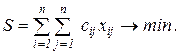(суммарные транспортные расходы минимальные)

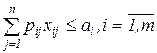(ограничения по грузоподъемности каждой транспортной единицы)

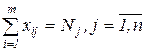(все рейсы должны быть выполнены)

хij ≥ 0, 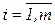, , 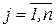хij – целые.

Задача о назначениях

Частным случаем транспортной задачи линейного программирования является задача о назначениях – задача выбора.

Это распределительная задача, в которой для выполнения каждой работы требуется один и только один ресурс (один человек, одна автомашина и т.п.), а каждый ресурс может быть использован на одной и только работе.

То есть, ресурсы не делимы между работами, а работы не делимы между ресурсами.

Задача о назначениях имеет место при назначении людей на должности, водителей на машины, транспортных средств на маршруты, при распределении групп по аудиториям, тем по подразделениям.

Исходные параметры модели

Имеется n работ и n кандидатов для их выполнения (механизмов). Производительность каждого механизма различна. Затраты i -го кандидата на выполнение j -ой работы равны c_ij (i, j = ).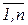

Пусть х_ij – переменная, значение которой равно 1, если i -й кандидат назначен выполнять j -ю работу и 0 – в противном случае.

Математическая модель.

Найти минимум целевой функции

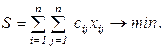
(в целевую функцию входят только те значения c_ij (i, j = 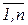), для которых х_ij отличны от нуля, т.е. входят затраты, соответствующие назначенным работам)

при ограничениях

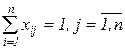(каждый кандидат выполняет только одну работу);

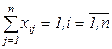(каждая работа может выполняться одним кандидатом);

х_ij Є {0; 1}, (i, j = ).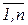

Решить задачу о назначениях – значит найти х_ij, удовлетворяющие ограничениям и доставляющим минимуму целевой функции.

Это транспортная задача, в которой правые части ограничений равны 1, а переменные могут принимать только два значения (0,1). Простая форма задачи позволила разработать для нее достаточно простые методы решения.

Дата добавления: 2014-11-29