Законы Ньютона

Основные фундаментальные законы механики

Рассмотрим систему, модель которой может быть представлена как материальная точка, система материальных точек (механическая система).

Материальная точка - тело, размеры и форма которого несущественны в рассматриваемой задаче.

Пример идеализации исходя из целей и задач.

Материальная точка не имеет размеров. Тогда что такое линия? Определение линии, плоскости: «Существует хотя бы одна прямая или одна плоскость. Каждая прямая и каждая плоскость есть несовпадающее с пространством непустое множество точек». Как не имеющие размеров точки могут заполнить линию? Вводится понятие предела и связанного с ним понятия бесконечно малой величины, непрерывности (основа дифференциального и интегрального исчисления).

Функция непрерывна на интервале, если она непрерывна во всех его точках, тогда ее график представляет собой непрерывную кривую.

Предел по ∆x: lim [f(x + ∆x) - f(x)] = 0.

Производная от функции y = f(x) в точке x есть скорость изменения ее в этой точке: lim ∆у/∆x = [f(x + ∆x) - f(x)] / ∆x = f′(x)

Траектория - линия, описываемая движущейся точкой. Состояние системы описывается точкой фазового пространства, которая тоже движется по некоторой траектории в этом пространстве. Состояние материальной точки не сводится к ее геометрическому положению, включает также и скорость.

Система материальных точек (механическая система) совокупность материальных точек, которая в общем случае взаимодействует как друг с другом, так и с другими телами, не включенными в систему.

В системе, представленной как абсолютно твердое тело расстояние между любыми точками постоянны (размеры и форма не изменяются при движении). Тело может быть представлено как система материальных точек, жестко связанных друг с другом.

Инерционные свойства механической системы выражаются первым и вторым законами Ньютона. Он первым понял, что ускорение, а не скорость объекта пропорциональна приложенной силе.

Инерционные свойства механической системы выражаются первым и вторым законами Ньютона.

Масса тела не зависит от скорости его движения - ускорение, а не скорость объекта пропорциональна приложенной силе.

1-ый закон - если на материальную точку не действуют внешние силы (другие тела), то она находится в состоянии покоя или равномерного прямолинейного движения.

Этот закон называют законом инерции движения материальных точки, свободной от внешних воздействий – движением по инерции. Любые изменения состояния движения обусловлены действием внешних сил.Под действием внешней силы точка приобретает конечное по величине ускорение, в отсутствие внешних воздействий – сохраняет состояние покоя или равномерного прямолинейного движения.

2-й закон - произведение массы тела на ускорение равно суме всех действующих на тело сил.

Закон устанавливает связь между действующей силой и вызванным ею изменением состояния (ускорением): ускорение материальной точки прямо пропорционально действующей на нее силе F ~ a.

Отношение силы к приобретенному ускорению постоянно для данного тела. Это отношение называется массой.

Масса = Сила / Ускорение

Здесь масса характеризует инерционные свойства материальной точки и называется инертной массой материальной точки.

Количество движения материальной точки – вектор К_i, равный произведению массы точки m_i на ее скорость v _i: К_i = m_i v _i:

Или: первая производная по времени от импульса (количества движения) материальной точки (системы точек) равна главному вектору F всех внешних сил, приложенных к точке:

d K _i/ d t = F _i или d/d t (m_i v _i) = F _i.

Или: элементарное изменение количества движения материальной точки равно элементарному импульсу действующей на нее силы:

d (m_i v _i) = F _i d t, так как m_i = const, то w _i = d v _i / d t = F _i / m_i.

Итак, второй закон Ньютона для материальной частицы m¨x = F.

Здесь m – масса частицы, x (t) = (x ₁(t), x ₂(t), x ₃(t)) – ее положение в момент времени t.

Частица движется в пространстве R³, x ₁(t), x ₂(t), x ₃(t) – ее координаты, F - действующая на частицу сила, может задаваться как функция времени F = F (t). Обычно сила задается как вектор-функция аргументов x Î R ³, x ˙ Î R ³ и времени t. Тогда уравнение второго закона есть векторное дифференциальное уравнение второго порядка mx ¨ = F (x, x˙, t).

Для того, чтобы описать движение материальной точки при помощи этого уравнения, недостаточно задать ее начальное положение, задание начальных условий должно включать и задание начальной скорости:

x (0) = x ₀, x ˙ (0) = v ₀.

Здесь x ₀ – начальное положение точки x ₀(t) = (x ₀₁, x ₀₂, x ₀₃) Î R ³, v ₀(t) = (v ₀₁, v ₀₂, v ₀₃) Î R ³ – ее начальная скорость.

Таким образом, фазовое пространство данной системы есть R ³ х R ³, а состояние системы – есть пара (x, v), где x - положение материальной точки, v - ее скорость.

Согласно первому и второму законам Ньютона все изменения состояния движения вызываются силами – силы являются причинами любого изменения.

Ускорение возникает в направлении действия силы. Силы инерции направлены в противоположную сторону. Возникают только в системе отсчета, движущейся с ускорением – это кажущиеся силы.

3-ий закон - две материальные точки действуют друг на друга с силами, равными по величине и направленными в противоположные стороны вдоль прямой, соединяющей эти точки.

F _ij = - F _ji.

F _ij - сила, действующая на i –ю точку со стороны j –ой точки.

Тяготение между телами осуществляется через гравитационное поле (поле тяготения), которое является одной из форм материи.

Здесь масса материальной точки характеризует гравитационные свойства этой точки и называется гравитационной массой (массой тяжести).

Для всех тел отношение их инертных и гравитационных масс постоянно. Инертные и гравитационные массы равны и связаны с силой тяжести тела соотношением m = F / g.

Векторная характеристика гравитационного поля – его напряженность g, которая равна отношению силы тяготения, действующей на материальную точку, к его массе: g = F / m.

Закон всемирного тяготения: между любыми двумя материальными точками действуют силы взаимного притяжения

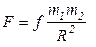, где f - гравитационная постоянная (сила взаимного притяжения между двумя точками одинаковой массы на расстоянии единицы длины).

Свойство притягивать тела обусловлено массой тела. Гравитационная сила – сила, с которой два тела притягиваются друг к другу (сила тяготения).

Каждое тело создает вокруг себя силовое поле – поле тяготения. Напряженность этого поля в любой его точке характеризует силу, которая действует на другое тело, находящееся в этой точке: g = F / m.

Закон сохранения массы – масса изолированной системы тел (или материальных точек) не изменяется при любых происходящих в ней процессах.

Масса тела – физическая величина, которая является мерой его инерционных и гравитационных свойств.

Масса – величина аддитивная, т.е. масса m любой системы материальных точек (например, твердого тела) равна сумме масс m_i всех n точек системы: m = .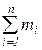

Центром инерции или центром масс системы материальных точек называется точка С (х _с, у _с, z _c), радиус-вектор r _c которой связан с массами m _i и радиус-векторами r _c всех n точек соотношением =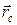

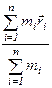
Дата добавления: 2014-11-29