Выбор математических методов

Выбор математических методов определяется поставленными задачами измерения. Фундаментальная теория измерения имеет два основных направления: физическое и математическое. Первое основано на тезисе о неизбежности погрешности измерения. Второе на абстракции «абсолютно точного» сравнения.

Требования к представлению результата измерения величины независимо от особенностей процесса измерения определяют следующие необходимые задачи обработки результатов наблюдения:

1. определение оценки математического ожидания;

2. определение среднего квадратичного отклонения; (дисперсии);

3. выполнение доверительного интервала;

4. оценка грубых погрешностей;

5. оценка и выбор закона распределения.

Предположим, что произведено n наблюдений x₁, x₂, x₃,…,x_n и точность получения х_i для любого i одинакова, то есть имеют место равноточные измерения. Тогда при нормальном законе распределения погрешностей, в качестве результата измерения принимаем среднее арифметическое значение

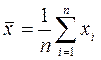
Для достаточно больших n можно ограничиться полученным результатом. Но часто при измерениях по разным соображениям n ограничено. Тогда необходимо указать доверительный интервал для 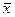. И во всех случаях 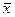не дает оценки точности процесса измерения. Для оценки точности измерения или рассеяния значений физической величины используют дисперсию σ² или среднее квадратичное отклонение σ.

При ограниченном n оценку σ определяют в виде:

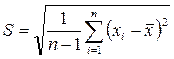
В качестве относительной характеристики рассеяния может использоваться коэффициент вариации:

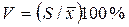
Он показывает насколько велико рассеяние по сравнению со средним значением. Значительная часть задач измерения ограничивается восстановлением зависимости по результатам измерения. При этом если вид функции распределения известен с точностью до постоянных, то задача сводится к косвенным измерениям. Но существует класс задач, когда характер кривой распределения трудно предположить, тогда обращаются к методу наименьших квадратов.

Дата добавления: 2014-12-10