Построение плоскости, касательной к кривой поверхности

Плоскостью, касательной к поверхности, называется плоскость, определяемая двумя прямыми, касательными к двум пересекающимся линиям, принадлежащим этой поверхности.

Возьмем отсек некоторой кинетической поверхности Ф и на ней точку А.(рисунок 10.1)

Рисунок 10.1

Через точку А проведем на поверхность две любые кривые f₁ и f₂. К этим кривым в точке А построим касательные t₁ и t₂. Плоскость, образованная этими касательными и называется касательной плоскостью Q к поверхности Ф в точке А.

В то же время через точку А поверхности проходит бесчисленное множество кривых, каждая из которых имеет свою касательную. Следовательно, касательная плоскость является геометрическим местом всех касательных, проходящих через данную точку поверхности.

Введем еще одно понятие – нормаль.

Прямая n, проходящая через точку касания А и перпендикулярная касательной плоскости Q, называется нормалью к поверхности. Отсюда нормальное сечение поверхности – это сечение плоскостью, проходящей через нормаль. Для построения нормали на эпюре используют условие перпендикулярности прямой и плоскости (см. гл.?).

Если в заданной точке поверхности можно построить единственную касательную, то такую точку называют обыкновенной.

Если в точке можно построить несколько касательных, то такую точку называют особой. Особыми точками является вершина конической поверхности и точка на ребре возврата.

Рассмотрим плоскости касательные к поверхности в обыкновенных точках.

В зависимости от вида поверхности плоскость может касаться поверхности в одной точке, по линии (прямой или плоской кривой) или, касаясь, может пересекать поверхность по некоторой линии. Каждая из этих точек имеет свое название.

Если касательная плоскость имеет с поверхностью только одну общую точку, то все линии поверхности, пересекающиеся в этой точке, расположены по одну сторону от касательной плоскости. Такую точку называют эллиптической. Поверхности, у которых все точки эллиптические, являются выпуклыми криволинейными поверхностями. К ним относятся сфера, тор, эллипсоид, параболоид.(точка А на рис. 10.1, 10.2)

Если касательная плоскость имеет с поверхностью общую прямую или плоскую кривую линию, то точки, принадлежащие этой линии, называются параболическими. Такие точки имеют цилиндр, конус, торс (касательная прямая), тор (касательная окружность m₁). (рис. 10.2)

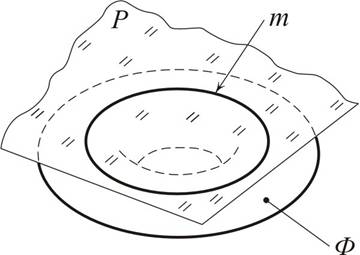
Рисунок 10.2

Если касательная плоскость имеет с поверхностью общую точку, но при этом пересекает поверхность по двум линиям, то такую точку называют гиперболической. Следовательно, гиперболическая точка принадлежит линии, по которой касательная плоскость пересекает поверхность. Каждый отсек поверхности, все точки которой являются гиперболическими, имеют седлообразную форму (винтовые поверхности, косая плоскость). У однополосного гиперболоида (рисунок 10.3) касательная плоскость Р в точке А пересекает поверхность по двум прямым m и n.

Рисунок 10.3

Геликоиды пересекаются касательной плоскостью по прямой и кривой, а тор по двум кривым. И вообще, тор является уникальной поверхностью, так как на этой поверхности имеются все три вида точек касания А, В и С. (рис. 10.4)

Рисунок 10.4

Горизонтальная плоскость Т касается тора по окружности m (m₁,m₂) – состоящей из параболических точек С. Эта окружность разделяет тор на две части: внутреннюю и наружную.

Наружная поверхность с точками А состоит из эллиптических точек, так как вся поверхность располагается по одну сторону от касательной плоскости Q.

Внутренняя поверхность с точками В состоит из гиперболических точек, так как касательная плоскость пересекает тор по двум кривым l с точкой самопересечения В.

Построение касательных плоскостей к поверхностям является основой теории теней. Касательными плоскостями пользуются для определения наиболее близких и удаленных точек от плоскостей проекций. Касательные плоскости применяют при построении очертаний поверхностей.

При построении касательной плоскости всегда задают некоторые условия для ее проведения. Возможны следующие шесть видов задач. Построить плоскость, касательную к поверхности и проходящую:

а) через точку на поверхности;

б) через точку вне поверхности;

в) через линию (прямую или кривую) на поверхности;

г) через прямую вне поверхности;

д) параллельно данной прямой;

е) параллельно данной плоскости.

В решении задач на построение касательных плоскостей часто используется известное положение – касательная к кривой в пространстве проецируется в касательную в проекции кривой.

Рассмотрим примеры построения касательных плоскостей к различным поверхностям.

10.1.1.Касательные плоскости к линейчатым поверхностям с параболическими точками.

Линейчатая поверхность с параболическими точками – это конус и цилиндр, каркас которых множество прямых – образующих.

Исходя из этого касательную плоскость можно определить двумя пересекающимися прямыми, из которых одна является образующей, проходящей через заднюю точку, а другая прямая касательная к любой построенной на поверхности кривой линии в точке пересечения ее с этой образующей. Чаще всего за эту кривую линию принимают очерк поверхности или параллель.

Пример 1. Построить плоскость касательную к конусу и проходящую через точку А, лежащую на его поверхности. Построить нормаль к этой поверхности. (рис. 10.5)

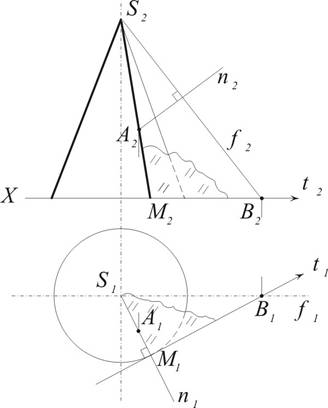
Рисунок 10.5

Касательная плоскость определяется образующей SM (S₁M₁, S₂M₂), проходящей через точку А и касательной t (t₁,t₂) к очерку конуса в точке М на плоскости П₁.Получилась касательная плоскость (SM∩t).

Чтобы построить нормаль n (n₁,n₂) надо в касательной плоскости провести горизонталь и фронталь. Касательная t является горизонталью. Проводим горизонтальную проекцию фронтали f₁ до пересечения с t₁ в точке В (В₁) и строим f₂. Затем проводим нормаль из точки А. (А₁n₁^t₁,А₂n₂^f₂).

Пример 2. Построить плоскость касательную к конусу и проходящую через точку D, расположенную вне конической поверхности (рис. 10.6)

Рисунок 10.6

В этом случае задача имеет два решения.

План решения: (алгоритм)

1. Через точку С и вершину S проводим прямую CS (C₁S₁,C₂S₂).

2. Находим горизонтальный след этой прямой M (M₁,M₂).

3. Через точку М проводим касательные t₁ и l₁ к очерку конуса (окружность).

4. Через точки касания А и В проводим образующие SA (S₁A₁, S₂A₂) и SB (S₁B₁, S₂B₂).

5. Пересекающиеся прямые t∩SA и l∩SB дают искомые касательные плоскости SAM и SBM.

Пример 3. Построить плоскость касательную к конусу и параллельную прямой КЕ. (рис. 10.7)

Рисунок 10.7

Здесь два решения. Рассмотрим алгоритм:

1. Через S проводим SM║KE и находим горизонтальный след М.

2. Через М проводим касательные t₁ и l₁ к основанию конуса.

3. Через точки касания А и В проводим образующие SA и SB.

4. t∩SA и l∩SB – дают искомые касательные плоскости SAt и SBl.

Пример 4. Построить плоскость касательную к цилиндру и параллельную данной прямой. (рис. 10.8)

Рисунок 10.8

Здесь также два решения. Рассмотрим алгоритм.

1. Так как искомой плоскости должна принадлежать одна из образующих цилиндра (линия касания) и прямая, параллельная данной ЕК, то для определения следов касательных плоскостей необходимо построить плоскость посредник Р параллельную и прямой ЕF и образующей цилиндра.

2. Плоскость Р зададим двумя пересекающимися прямыми KC║EF и KD║ образующей (P=KC∩KD).

3. Переходим от задания плоскости прямыми к заданию следами. Находим C₁ и D₁ и проводим горизонтальный след Р₁, а через Р_Х и N₂ фронтальный след Р₂.

4. Горизонтальные следы искомых касательных плоскостей будут параллельны горизонтальному следу Р₁, поэтому проводим касательные t₁ и l₁ к очерку цилиндра параллельно Р₁.

5. В точках касания А и В проводим образующие А1 и В2.

6. Пересекающиеся прямые А1∩t и В2∩l задают искомые касательные плоскости к цилиндру.

10.1.2. Касательные плоскости к не линейчатым поверхностям с эллиптическими точками.

Для построения касательной плоскости в заданной точке поверхности вращения, прежде всего, необходимо через заданную точку провести по поверхности две кривые линии. Касательные прямые к ним и определяют искомую касательную плоскость. За кривые линии обычно принимают параллель (окружность) и меридиан.

Пример 5. Построить плоскость касательную к тору в точке D. (рис. 10.9)

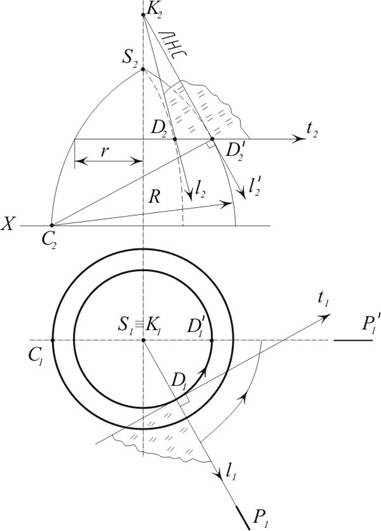
Рисунок 10.9

Рассмотрим алгоритм решения:

1. Через точку D (D₁,D₂) проводим параллель радиуса r и горизонтальную проекцию меридиана S₁D₁

2. Проводим касательную к параллели D₂t₂║X, D₁t₁^S₁D₁.

3. Горизонтальная проекция касательной l₁ совпадает с горизонтальной проекцией меридиана S₁D₁≡l₁.

4. Для построения фронтальной проекции касательной l₂ , меридиональную плоскость Р ₁, проходящую через точку D, повернем вокруг вертикальной оси в положение Р₁║П₂, то есть до совмещения с главным меридианом. Точка D при этом займет положение D`<sub>1</sub>, D`₂.

5. Проводим через проекцию D`<sub>2</sub> касательную к главному меридиану (l`₂^C₂D`₂) и продолжим ее до пересечения с осью в точке К₂. Эта касательная является в то же время и линией наибольшего ската (Л.Н.С.) касательной плоскости.

6. При возвращении плоскости Р в первоначальное положение точка К остается неподвижной.

7. Соединив К₂ и D₂ получим фронтальную проекцию касательной l (l₂).

8. Две пересекающиеся касательные t и l определяют единственную плоскость к тору в точке D.

Пример 6. Построить плоскость касательную к сфере в точке А на ее поверхности. (рис. 10.10)

Рисунок 10.10

Известно, что радиус сферы СА, проведенный в точку касания, является нормалью сферической поверхности. Поэтому задача сводится к построению плоскости перпендикулярной радиусу СА.

Строим плоскость, задавая ее горизонталью ht и фронталью fl, перпендикулярными к радиусу СА (f₂l₂^C₂A₂, h₁t₁^C₁A₁).

Эти пересекающиеся прямые t∩l и определяют плоскость, касательную к сфере в точке А.

Пример 7. Построить плоскость касательную к сфере и проходящую через точку S, не принадлежащую поверхности сферы. Точка S расположена в горизонтальной экваториальной плоскости сферы. (рис.10.11)

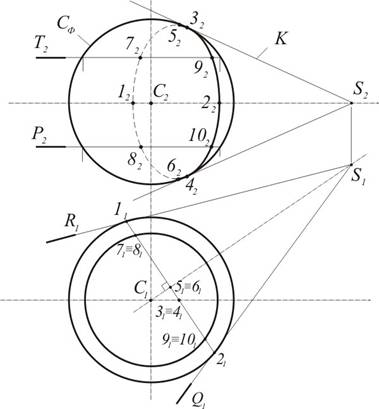
Рисунок 10.11

1. Через точку S вне поверхности сферы можно провести множество плоскостей касательных к сфере. Поверхностью, огибающей это семейство плоскостей, является некоторая коническая поверхность взаимокасательная со сферой.

2. Эта коническая поверхность, описанная вокруг сферы, касается ее по окружности взаимокасания 1-3-2-4^SC. Поэтому любая плоскость, которая касается конуса по образующей, будет касаться и сферы в единственной точке, общей для конуса и сферы и лежащей на окружности взаимокасания.

3. Задача в данном варианте имеет бесчисленное множество решений (если нет ограничивающих условий).

4. Из проекций заданной точки S (S₁,S₂) проводим касательные к окружностям экватора и меридиана сферы. Получаем точки 1, 2, 3, 4.

5. Горизонтальная проекция окружности взаимокасания проецируется в отрезок прямой 1₁2₁^S₁C₁ (так как ось вращения SС║П₁).

6. Фронтальной проекцией окружности взаимокасания является эллипс, малая ось которого отрезок 1₁2₂, а большая ось – фронтальная проекция 5₂6₂ диаметра окружности параллельного плоскости П₂ (5₂6₂=1₁2₁).

7. промежуточные точки эллипса определяются с помощью параллелей сферы Т, Р… (точки 7,8,9,10).

8. Любая касательная плоскость к сфере задается образующей и касательной к окружности основания вспомогательного конуса. Например, плоскости R и Q являются касательными к сфере через точку S. (R и Q^П₁)

9. Другие касательные плоскости легко построить, если ось вращения вспомогательного конуса SC сделать проецирующей (метод перемены плоскостей проекций), а затем решать как в примере 10.6.

10.1.3. Касательные плоскости к линейчатым поверхностям с гиперболическими точками.

У не развертывающихся линейчатых поверхностей гиперболического гиперболоида или однополостного гиперболоида - через каждую точку поверхности проходят две образующие, принадлежащие к различным семействам. Эти образующие и определяю касательную плоскость в каждой точке поверхности. Касательная плоскость, прикасаясь к поверхности в точке Е (рис. 10.12), пересекает поверхность по образующим PQ и MN, проходящим через эту точку.

Часть поверхности лежит по одну сторону касательной плоскости, а другая часть поверхности – по другую сторону. В каждой точке образующей будет новая касательная плоскость.

Рисунок 10.12

Дата добавления: 2014-11-29