Теорема о рациональных корнях многочлена

Если многочлен

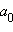с целыми коэффициентами имеет рациональный корень то число p является делителем числа (свободного члена), а число q является делителем числа (старшего коэффициента).

Доказательство

Пусть все коэффициенты многочлена являются целыми числами, и пусть целое число a является корнем этого многочлена. Так как в этом случае 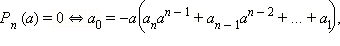то отсюда следует, что коэффициент 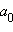делится на a.

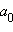Замечание. Эта теорема фактически позволяет находить корни многочленов высших степеней в том случае, когда коэффициенты этих многочленов − целые числа, а корень − рациональное число. Теорему можно переформулировать так: если нам известно, что коэффициенты многочлена − целые числа, а корни его − рациональны, то эти рациональные корни могут быть только вида где p является делителем числа (свободного члена), а число q является делителем числа (старшего коэффициента).

Теорема о целых корнях, заключающая в себе

Если целое число α - корень многочлена с целыми коэффициентами, то α - делитель его свободного члена.

Доказательство. Пусть:

P (x)=a₀xⁿ +a₁xⁿ^-1+…+a_n-1x +a_n

многочлен с целыми коэффициентами и целое число α −его корень.

Тогда по определению корня выполняется равенство P (α)=0;

a₀ αⁿ+a₁ αⁿ^-1+…+a_n-1 α +a_n=0.

Вынося общий множитель α за скобки, получим равенство:

α(a₀ αⁿ^-1 +a₁ αⁿ^-2 +…+a_n-1)+a_n=0, откуда

a_n= -α(a₀ αⁿ^-1 +a₁ αⁿ^-2 +…+a_n-1)

Так как числа a₀, a₁,…a_n-1, an и α −целые, то в скобке стоит целое число, и, следовательно, a_n делится, на α, что и требовалось доказать.

Доказанная теорема может быть сформулирована и следующим образом: всякий целый корень многочлена с целыми коэффициентами является делителем его свободного члена.
На теореме основан алгоритм поиска целых корней многочлена с целыми коэффициентами: выписать все делители свободного члена и поочерёдно выписать значения многочленов этих чисел.

2.Дополнительная теорема о целых корнях

Если целое число α−корень многочлена P(x) с целыми коэффициентами, то α-1−делитель числа P(1), α+1−делитель числа P(-1)

Доказательство. Из тождества

xⁿ-yⁿ=(x-y)(xⁿ^-1+xⁿ^-2y+…+ xyⁿ^-2+yⁿ^-1)

вытекает, что для целых чисел b и c число bⁿ-cⁿ делится на b∙c. Но для любого многочлена P разность

P (b)-P(c)= (a₀bⁿ+a₁bⁿ^-1+…+a_n-1b+a_n)-(a₀cⁿ+a₁cⁿ^-1+…+a_n-1c+a_n)=

=a₀(bⁿ- cⁿ)+a₁(bⁿ^-1-cⁿ^-1)+…+a_n-1(b-c)

и, следовательно, для многочлена P с целыми коэффициентами и целых чисел b и c разность P(b)-P(c) делится на b-c.

Затем: при b = α, с=1, P (α)-P (1)= -P(1), а значит, P(1) делится на α-1. Аналогично рассматривается второй случай.

Схема Горнера

Теорема: Пусть несократимая дробь p/q является корнем уравнения a₀xⁿ+a₁xⁿ⁻¹+ +a_n−1x+a_n =0 c целыми коэффициентами, тогда число q является делителем старшего коэффициента a0, а число р является делителем свободного члена a_n.

Замечание 1. Любой целый корень уравнения с целыми коэффициентами является делителем его свободного члена.

Замечание 2. Если старший коэффициент уравнения с целыми коэффициентами равен 1, то все рациональные корни, если они существуют - целые.

Корень многочлена. Корнем многочлена f(x)= a₀xⁿ+a₁xⁿ⁻¹+ +a_n−1x+a_n является x = c, такое, что f (c)=0.

Замечание 3. Если x = c корень многочлена f(x)=a₀xⁿ+a₁xⁿ⁻¹+ +a_n−1x+a_n, то многочлен можно записать в виде: f(x)=(x−c)q(x), где q(x)=b₀xⁿ⁻¹+b₁xⁿ⁻²+ +b_n−2x+b_n−1 это частное от деления многочлена f(x) на одночлен x - c

Деление многочлена на одночлен можно выполнить по схеме Горнера:

Если f(x)=a₀xⁿ+a₁xⁿ⁻¹+ +a_n−1x+a_n, a₀≠0, g(x)=x−c, то при делении f (x) на g (x) частное q(x) имеет вид q(x)=b₀xⁿ⁻¹+b₁xⁿ⁻²+ +b_n−2x+b_n−1, где b₀=a₀,

b_k=c b_k−1+a_k, k=1, 2, ,n−1. Остаток r находится по формуле r=c b_n−1+a_n

	a0	a1	a2	...	an−1	an
x = c	b0=a0	b1=c b0+a1	b2=c b1+a2	...	bn−1=c bn−2+an−1	r=c bn−1+an

В первой строке этой таблицы записывают коэффициенты многочлена f(х). Если какая-то степень переменной отсутствует, то в соответствующей клетке таблицы пишется 0. Всегда старший коэффициент частного равен старшему коэффициенту делимого b₀=a₀. Если x = c является корнем многочлена, то в последней клетке получается 0, т.е. остаток от деления будет равен нулю.

Пример. Решить уравнение x³−x²−8x+12=0

	a0=1	a1=−1	a2=−8	a3=12
x = 1			-8		не корень
x = -1		-2	-6		не корень
x = 2			-6		корень

Решение: Коэффициент при старшей степени равен 1, поэтому целые корни уравнения надо искать среди делителей свободного члена: 1; 2; 3; 4; 6; 12. используя схему Горнера, найдем целые корни уравнения:

Если один корень подобран по схеме Горнера. то можно дальше решать так x³−x²−8x+12=(x−2)(x²+x−6)=0 (x−2)²(x−3)=0 x=2;x=3

Дата добавления: 2014-12-16