Понятие о КПД машинного агрегата

Для характеристики установившегося режима вводится важное понятие. Чтобы определить его рассмотрим более подробно работу А_с, которую совершают силы сопротивления. Очевидно что А_с состоит из работы которую совершают силы полезного сопротивления А_пс (для преодоления которых и создана машина), а также работы, которую совершают силы трения в кинематических парах и сила сопротивления среды А_т .

А_с = А_пс + А_т. Из вышесказанного следует (см. понятие цикла работы)

A_g = A_пс + А_т (1)

Или

1 = η + ξ (2)

Где - механический КПД машинного агрегата

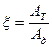- механический коэффициент потерь МА

Из (2) следует, что 0 ≤ η < 1, 0 < ξ ≤ 1, где знак = относится к режиму холостого хода (т.е. нет полезной нагрузки)

КПД – важная характеристика машины, так как в среднем показывает насколько она экономична, энергетически целесообразна. Поскольку точное определение η зависит от точности определяемых сил трения или сопротивления среды (а это достаточно сложно), его величина находится, как правило экспериментально.

Только для некоторых простых механизмов можно теоретически определить КПД

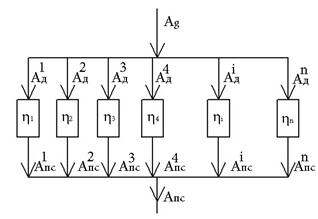
Если МА можно представить в виде совокупности простых механизмов (или механизмов с известным КПД), соединенных последовательно, параллельно или смешанным образом, возможна теоретическая оценка его общего КПД

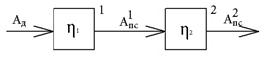
А) Последовательное соединение

Из определения следует:

, ,

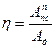Где - КПД всей машины; ₁ – КПД первого механизма; _i – КПД i-го механизма;

С другой стороны, очевидно, что

Окончательно

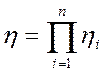(3)

Б) Параллельное соединение

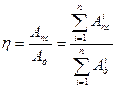(4)

В зависимости от того какую работу легче определить на практике (4) можно представить

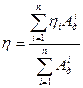или (5)

Если схема машинного агрегата представляет собой цепь последовательных и параллельных соединений то пользуются зависимостями (3) и (5)

На практике работу определить значительно сложнее, и лучше оперировать понятием «мощность механизма» N (работа в единицу времени)

Тогда имеем зависимость для КПД аналогичные (3) и (5) только вместо А имеем N

1. Исследование движения машинных агрегатов под действием сил и моментов

Постановка задачи:

Любой машинный агрегат можно представить в виде блок-схемы

Задача исследования движения МА является задачей отыскания действительного закона движения звеньев МА, который бы учитывал не только действие на него внешних сил и моментов, но также и взаимное влияние механизмов входящих в машинный агрегат.

Существует 2 пути решения задачи:

1.Разбиение всего МА на отдельные звенья, составление уравнений движения этих звеньев (в форме уравнений Лагранжа 2-го рода или второго закона Ньютона) и решение полученной системы дифференциальных уравнений. Этот способ применяется для исследования для исследования динамики конкретных машин. Решение очень сложное, т.к. эта система нелинейных дифференциальных уравнений и в правой части содержатся неизвестные реакции связей, действующие в кинематических парах.

2.Второй путь основан на рассмотрении МА как некоторой дискретной механической системы, обладающей несколькими степенями свободы. Для подавляющего большинства МА ω=1. Для них целесообразна замена МА некоторой условной механической системой с одной степенью свободы. Эта условная механическая система, с ω=1, получила название динамической модели МА (расчетная схема для решения поставленной задачи) или звена приведения.

Рассмотрим виды динамических моделей МА с одной степенью свободы.

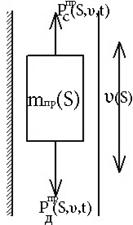
Для плоских механизмов в расчетной практике используется 2 вида моделей. Эти модели применяются в зависимости от того какое движение совершает звено приведения: вращательное или поступательное. Условные параметры обозначенные на рисунке получили название приведенных параметров.

Искомые функции, характеризующие закон движения звена приведения ω, v. Наиболее удобно в качестве звена приведения выбирать звено МА, движение которого описывается одной обобщенной координатой (это, как правило входное звено). В этом случае можно сразу найти его реальный закон движения, а далее, реальные законы движения остальных звеньев

Рассмотрим как находятся приведенные параметры моделей представленных выше:

Для определения приведенных инерциальных параметров J_пр; m_пр используют равенство кинетической энергии звена приведения и кинетической энергии реальной машины:

E_пр = E_р.м. (1)

Для 1-ой модели:

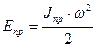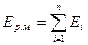, (2)

Где Ei – кинетическая энергия i-го звена машины. В общем случае звено совершает плоскопараллельное движение, поэтому

(3)

Первое слагаемое определяет кинетическую энергию звена в поступательном и второе во вращательном движении относительно полюса, в выражении (3) за полюс выбран центр тяжести i-го звена S_i, так как в этом случае просто определить момент инерции звена J_si, а m_i, v _si, ω_i - соответствующая масса, скорость полюса, абсолютная угловая скорость i-го звена. Подставляя соотношения (2), (3) в (1) получим:

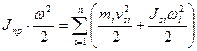
(4)

Из (4) следует, что J_пр является только функцией положения при постоянных m_i и J_si. Аналогично для второй модели получим, учитывая что

(5)

Приведенные силовые параметры () находятся из условия равенства элементарных работ совершаемых приведенными силовыми параметрами и внешними силами и моментами, действующими на звенья агрегаты:

dА_пр = dА_рн (6)

Для 1-ой модели:

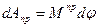; (7)

Для машин в общем случае удобнее оперировать не с работой, а с мощностью (как отмечалось уже ранее), поэтому поделим (7) на dt и получим

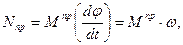
(8)

Мощность N_i, развиваемую силами приложенными к i-му звену, представим

(9)

Где P_i – сила, действующая на i-е звено, v _i – скорость точки приложения силы P_i, α_i – угол между ними; M_i – момент сил, действующий на i-е звено. Подставляя (7), (8), (9) в (6) находим

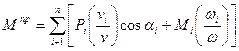
В общем случае из (10) следует, что M^пр является функцией положения (φ) и P_i и M_i, которые, в свою очередь, являются функциями t; φ; ω т.е. М^пр=f(φ,ω,t)

Аналогично получим приведенную движущую силу или силу сопротивления

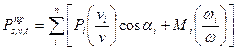
В качестве примера рассмотрим простейший машинный агрегат, где за звено приведения примем кривошип 1, учитывая (4) получим:

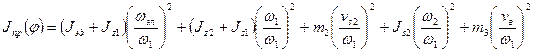, где

J_эд, J_z1, J_z2, J_s1, J_s2 – моменты инерции ротора эд.дв., зубчатых колес z₁, z₂,

Звенья 1,2 относит. Центров тяжести; m₂,m₃ – массы 2,3 звеньев, точка S₁ совпадает с O

Учитывая (10) имеем:

(движущих сил)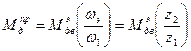

сил сопротивления

Дата добавления: 2014-12-16