Подготовка лабораторной установки к работе

Биения

Предположим, что маятники могут совершать колебания только в одной плоскости, т.е. имеют одну степень свободы. В этом случае при различных частотах уравнения колебаний для двух упруго связанных маятников можно записать в виде:

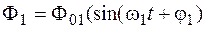; (5.3)

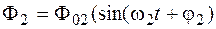), (5.4)

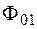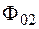где и – амплитуды колебаний первого и второго маятников, соответственно; 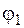и 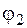– начальные фазы первого и второго маятников, соответственно.

Результатом сложения может оказаться апериодический процесс, если частоты 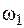и 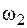не соизмеримы между собой. Если же частоты соизмеримы между собой, тогда можно найти такую частоту w₀, что выполняются соотношения

w₁ = m w₀; (5.5)

w₂ = n w₀, (5.6)

где m и n – целые числа.

В простейшем случае, когда А ₀₁ = А ₀₂ = А ₀, уравнение результирующего колебания, полученное путем сложения двух начальных, будет иметь вид

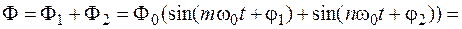
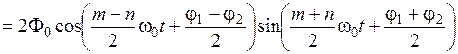. (5.7)

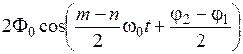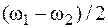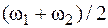Из последнего выражения видно, что множитель представляет собой амплитуду результирующего колебания, зависящую от времени и изменяющуюся с частотой , а – частота результирующего колебания. В случае, есл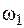и и 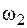близки по абсолютной величине, при этом Dw<<w₁, 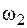, где 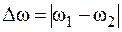, тогда результирующее колебание будет иметь вид, представленный на рис. 5.4.

Как видно из рис. 5.4, амплитуда результирующего колебания является функцией времени. Такие колебания называются биениями, а частота 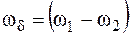называется циклической частотой биения.

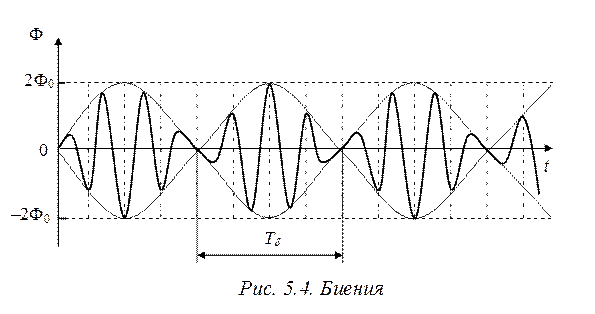
Период биений определяется соотношением

. (5.8)

3.3.1. Подключите прибор к питающей сети.

3.3.2. Установите одинаковые грузы m ₁ =m ₂ =m на обоих маятниках, на одном и том же расстоянии от оси колебаний.

3.3.3. Нажмите клавишу «сеть» и проверьте свечение лампочки фотоэлектрического датчика и индикаторов измерителя.

3.3.4. Включите питание двигателя и, плавно вращая ручку регулятора частоты, проверьте, работает ли двигатель и колеблется ли маятник.

Дата добавления: 2014-12-16