Правила выполнения сетей Петри

Выполнением сети Петри управляют количество и распределение фишек в сети. Фишки находятся в кружках и управляют выполнением переходов сети. Сеть Петри выполняется посредством запусков переходов. Переход запускается удалением фишек из его входных позиций и образованием новых фишек, помещаемых в его выходные позиции.

Переход может запускаться только в том случае, когда он разрешён.

Переход называется разрешённым, если каждая из его входных позиций имеет число фишек большее или равное числу дуг из позиции в переход. Кратные фишки необходимы для кратных входных дуг.

Фишки во входной позиции, которые разрешают переход, называются его разрешающими фишками. Например, если позиции p₁ и p₂ служат входами для перехода t₄, тогда t₄ разрешён, если p₁ и p₂ имеют хотя бы по одной фишке. Для перехода t₇ с входным комплектом {p₆, p₆, p₆} позиция p₆ должна обладать по крайней мере тремя фишками, для того чтобы t₇ был разрешён.

Определение 4. Переход t_j Î T в маркированной сети Петри С = { Р, Т, I, O } с маркировкой m разрешён, если для всех p_i Î P

.

Переход запускается удалением всех разрешающих фишек из его входных позиций и последующим помещением в каждую из его выходных позиций по одной фишке для каждой дуги. Кратные фишки создаются для кратных выходных дуг. Переход t₃ с O(t₃)= { p₇, p₁₃ } и I (t₃) = { p₂ } разрешён всякий раз, когда в p₂ будет хотя бы одна фишка. Переход t₃ запускается удалением одной фишки из позиции p₂ и помещением по одной фишки в позиции p₇ и в p₁₃ (его выходы). Дополнительные фишки в позиции p₂ не влияют на запуск t₃ (хотя они могут разрешать дополнительные запуски t₃).

Переход t ₂, в котором I (t ₂) = { p ₂₁, p ₂₃} и O (t ₂) = { p ₂₃, p ₂₅, p ₂₅} запускается удалением одной фишки из p ₂₁ и одной фишки из p ₂₃, при этом одна фишка помещается в p ₂₃ и две – в p ₂₅ (так как p ₂₅ имеет кратность, равную двум).

Запуск перехода в целом заменяет маркировку m сети Петри на новую маркировку 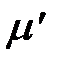. Заметим также, что так как можно запустить только разрешённый переход, то при запуске перехода количество фишек в каждой позиции всегда остаётся неотрицательным. Запуск перехода никогда не удалит фишку, отсутствующую во входной позиции. Если какая-либо входная позиция перехода не обладает достаточным количеством фишек, то переход не разрешён и не может быть запущен.

Определение 5. Переход t_j маркированной сети Петри с маркировкой m может быть запущен всякий раз, когда он разрешён. В результате запуска разрешённого перехода t_j образуется новая маркировка 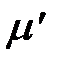, определяемая следующим соотношением: .

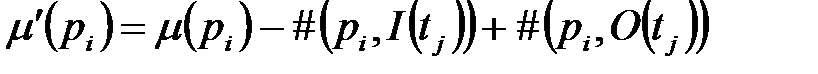Дата добавления: 2014-12-16