Методические рекомендации к выполнению КР

Основные теоретические сведения

1. Уравнение вида 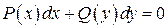называется дифференциальным уравнением с разделяющимися переменными. Его общим интегралом будет

.

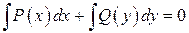2. Дифференциальное уравнение 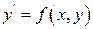называется однородным относительно переменных и 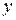, если 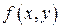- однородная функция нулевого измерения относительно своих аргументов, т.е. 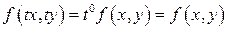. Данное уравнение с помощью замены 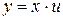сводится к уравнению с разделяющимися переменными.

3. Уравнение 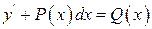называется линейным дифференциальным уравнением. Общее решение уравнения находим по формуле

.

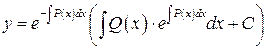4. Уравнение вида

,

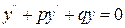где 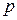и 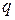- постоянные числа называется линейным однородным дифференциальным уравнением второго порядка. Квадратное уравнение 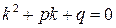называется характеристическим уравнением.

Если корни 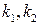характеристического уравнения действительны и различны, то общий интеграл уравнения 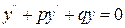выражается формулой

.

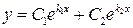Если , то общий интеграл уравнения 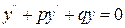находится по формуле

.

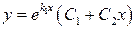Если 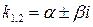, то общее решение уравнения 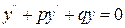находится по формуле

.

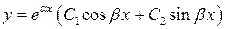5. Уравнение вида

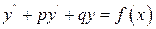
называется неоднородным линейным уравнением второго порядка. Если 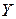- общее решение соответствующего однородного уравнения, - частное решение уравнения 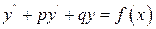, то общее решение уравнения 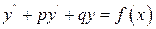имеет вид .

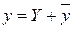Укажем правило нахождения частного решения уравнения 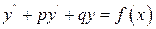методом неопределенных коэффициентов.

Пусть 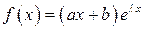, тогда

1) 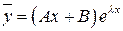, если 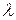не является корнем характеристического уравнения;

2) 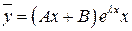, если 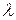является простым корнем характеристического уравнения;

3) 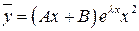, если 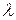двукратным корнем характеристического уравнения.

Пусть 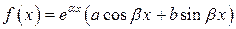, тогда:

1) 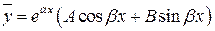, если число 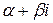является корнем характеристического уравнения;

2) 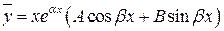, если число 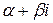не является корнем характеристического уравнения.

Пример 1. Найти общее решениеуравнения

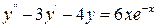- НДУ

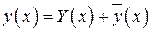- структура общего решения НДУ.

Характеристическое уравнение 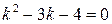имеет корни , .

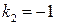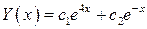- общее решение ОДУ.

По функции 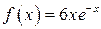запишем структуру частного решения .

.

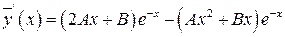Найденные выражения 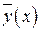, , 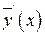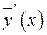подставляем в исходное уравнение и, разделив обе его части на 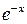, получаем уравнение

.

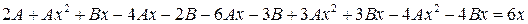Приравнивая коэффициенты при 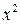, , 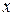, 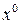получаем систему, решая ее находим 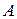и .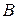

.

, .

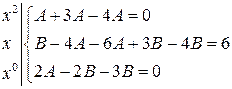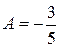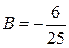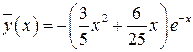- частное решение НДУ.

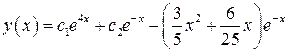- общее решение ОДУ.

Пример 2. Найти решение дифференциальных уравнений методом характеристического уравнения.

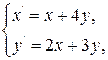
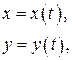
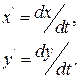
Решение. Частное решение системы будем находить в следующем виде 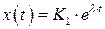, 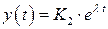. Требуется определить постоянные 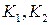и 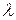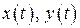удовлетворяли заданной системе уравнений. Подставляя их в систему и сокращая на 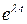, получим систему уравнений:

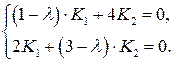
Составляем характеристическое уравнение и решаем его:

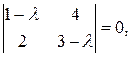
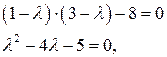
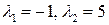- корни характеристического уравнения.

Корню 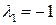соответствует система

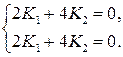или .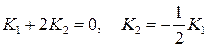

Полагаем 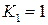, тогда 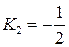. Получаем решение системы:

, .

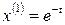Корню 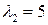соответствует система

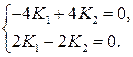или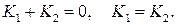

Получаем 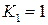, тогда 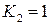. Получим решение системы:

, .

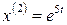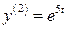Общее решение исходной системы имеет вид

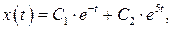
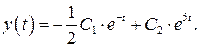
1. Достаточные признаки сходимости числовых рядов с положительными членами:

Признаки сравнения. Если даны два ряда

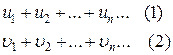
и для всех 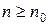выполняются неравенства 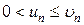, то:

1) из сходимости ряда (2) следует сходимость ряда (1);

2) из расходимости ряда (1) следует расходимость ряда (2).

Признак Даламбера. Если в знакоположительном ряде

существует предел 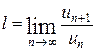, то:

1) ряд сходится, если ;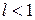

2) ряд расходится, если ;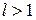

3) если 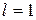, то признак Даламбера не дает ответа на вопрос о сходимости ряда.

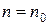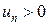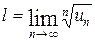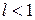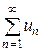Признак Коши. Если начиная с некоторого номера , и , то при ряд сходится, а при 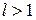расходится.

При 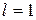признак Коши неприменим.

Интегральный признак Коши. Пусть члены ряда 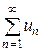монотонно убывают и функция 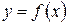непрерывная при 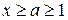, такова, что 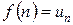. Тогда ряд 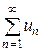и интеграл 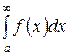одновременно сходится или расходится.

2. Сходимость знакочередующихся рядов исследуется с помощью признака Лейбница:

Если для знакочередующегося ряда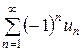

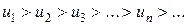и 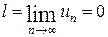, то данный ряд сходится и его сумма 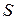удовлетворяет условию .

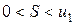3. Выражение вида 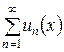называется функциональным рядом. Он называется сходящимся в точке 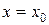, если сходится числовой ряд 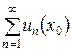. Множество значений 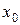, при которых ряд 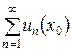сходится, называется областью сходимости ряда. Примером функционального ряда является степенной ряд 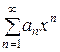. радиус сходимости степенного ряда определяется формулой

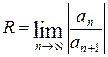или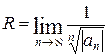

Интервал 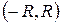называется интервалом сходимости степенного ряда.

Пример 3. Найти область сходимости степенного ряда .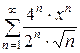

Решение. Радиус сходимости степенного ряда определяется по формуле:

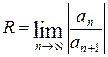
Так как

, ,

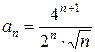то

.

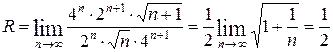Степенной ряд сходится в интервале .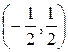

Исследуем поведение ряда на концах интервала.

При имеем 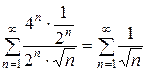, данный ряд сходится.

При 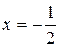имеем 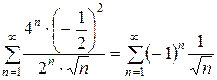, ряд сходится по признаку Лейбница, причем сходится условно. Следовательно, область сходимости ряда является полуинтервал .

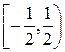Пример 4. Вычислить 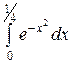с точностью до 10^-4.

Решение. Разложение подынтегральной функции в степенной ряд имеет вид:

.

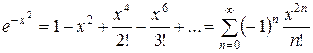Интегрируя этот ряд почленно, получим

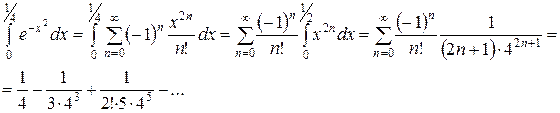
Полученный числовой ряд есть ряд Лейбница. Погрешность происходящая от отбрасывания всех членов начиная с третьего, будет по абсолютной величине меньше третьего члена:

.

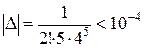Вычисляя с точностью до 0,0001, найдем

.

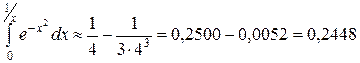Дата добавления: 2014-12-16