Основные пределы

Раскрытие неопределенностей

НАНОИНЖЕНЕРИЯ

Приёмная комиссия 32-82-23

МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА

Физика

Комплекс К-402.2. Методические указания по самостоятельной работе для подготовки к выполнению лабораторных работ по разделу физики «Молекулярная физика и термодинамика»

для студентов всех специальностей

Подписано в печать 03.12.2008. Формат 60×84/16.

Бумага офсетная. Отпечатано на ризографе. Уч.-изд. л. 2,0.

Тираж 160 экз. Заказ.

ГУ КузГТУ. 650026, Кемерово, ул. Весенняя, 28.

Типография ГУ КузГТУ. 650099, Кемерово, ул. Д. Бедного, 4а.

Деканат физико-

технологического факультета 32-82-63

Кафедра нанотехнологий 30-79-46

ФИЗИКО-ТЕХНОЛОГИЧЕСКИЙ ФАКУЛЬТЕТ

Направление

Профиль подготовки

«Нанотехнологии и наноматериалы»

Квалификация

«бакалавр»

(экзамены ЕГЭ: русский язык,

математика и физика)

Для раскрытия неопределенностей используют следующее:

1. упрощают выражение функции: раскладывают на множители, преобразовывают функцию с помощью формул сокращенного умножения, тригонометрических формул, домножают на сопряженное, что позволяет в дальнейшем сократить и т.д., и т.п.;

2. замечательные пределы - первый замечательный предел и второй замечательный предел;

1. Первый замечательный предел: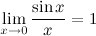

2. Второй замечательный предел:

7. Приращение функции и приращение аргумента.

На оси Х – две точки: x ₀ и x ₁ (рис.1). Если от x ₁ отнимем x ₀, то узнаем длину шага между ними – а говоря иначе, узнаем, на сколько приросла точка x ₀ в точке x ₁. Эта разность между двумя заданными точками оси X и называется приращением аргумента.

Точки x ₀ и x ₁ образуют на оси Y соответственно точки у ₀ и у ₁. Если от у ₁ отнять у ₀, то мы получим приращение функции.

Итак, в функции y = f (x) относительно определенных точек x ₀ и x ₁:
разность x ₁ – x ₀ называется приращением аргумента, а разность у ₁ – у ₀ называется приращением функции.

Но у ₀ и у ₁ – зависимые переменные (зависимые от значений х). То есть их правильно записывать так: f (x ₀) и f (x ₁). Следовательно, приращение функции – это разность f (x ₁) – f (x ₀).

Приращение обозначается греческой буквой Δ (дельта):

Δ x = x ₁ – x ₀;

Δ y (или Δ f) = f (x ₁) – f (x ₀).

Можно сказать и иначе: если к x ₀ прибавить величину приращения Δ x, то мы получим точку x ₁.
То есть x ₁ = x ₀ + Δ x (рис.2).
Тогда точку f (x ₁), отмеченную на первом рисунке как у ₁, тоже можно обозначить иначе:
f (x ₀ + Δ x).

Осталось вывести формулу приращения функции.

Формула приращения функции:

Δ y = f (x ₀ + Δ x) – f (x ₀) или Δ f = f (x ₀ + Δ x) – f (x ₀)

8. Производная функции.

9 Правила дифференцирования.

10 Формулы дифференцирования.

Производная функции у= f( х) в точках х называется предел(если существует и конечен) отношения приращения функции к приращению аргумента при условии что последний стремится к нулю.

Процесс нахождения производной называется дифференцирования.

Формулы дифференцирования:

Дата добавления: 2014-12-16