Неполная индукция. Популярная индукция

В-»А

АлВ

А,В

А

AvB

Импликация:

Отрицание:

Эквиваленция:

AvB

А

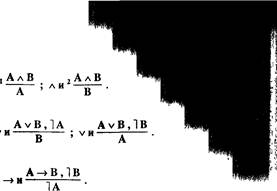
НА ' А •

А=В

(А->В)л(В-»А) '

Кроме этих прямых правил получения новых строк вывода, в СНВ приняты непрямые правила, определяющие стратегию построения вывода. Например, если нужно вывести из посылок формулу вида импликации (xi —> (xz —>...(xn-i -> Хп))), то после выписывания посылок выписываются в качестве допущений все антецеденты заключения, начиная с антецедента главного знака импликации, т.е. xi, •m, хз,..., Xn-i. Г,А->В

Если при этом удастся вывести Хп, то по непрямому правилу -> в,

^собираем

Г-»А->В

последовательно формулы: (xn-i-^Xn) (при этом исключается допущение Xn-i), (хп-2 —> (Xn-i —> Xn)(xn-r исключается из числа допущений) и т.д., пока не получим требуемое заключение xi -»(хп-2 —>... (Xn-i —> Хп). Это правило построения прямого вы­вода.

Приведем пример вывода с применением этого правила:

((pAq)->r) |_ (p-> (q ->r)

1. (р л q) —> г — посылка

2. р — допущение

3. q — допущение

4. р л q (2, 3. л в)

5.г(1,4,^„)

6. q -> г(3,5, ^в)(-3)

7.p^(q^r)(2,6, -^.)(-2)

Другое непрямое правило используется для построения косвенного вывода, при котором допущением является отрицание В или отрицание последнего консеквен-

_ Г,А->(Вл1В)

та Хп. Это правило имеет вид —————-———— и говорит о том, что если из каких-то Г—> |А

формул (Г) и допущения (А) получено противоречие (В л ТВ), то из этих формул следует ча. Таким образом, если строится косвенный вывод формулы вида (xi —> (х2 —>...(xn-i —> Хп)...), то после посылок выписываются формулы:

X] 1

допущения

Х2

Xn-i

^п

допущение косвенного доказательства [ДКД]

Затем по правилам вывода получаем следствия из всех имеющихся посылок и допущений до тех пор, пока не получим две противоречащие друг другу формулы'('В и 1В), что свидетельствуе! о несовместимости допущения косвенного доказательства с другими допущениями и посылками. Отсюда делается вывод о его ложности. Тогда в вывод вписывается строка 11 Хп, и тем самым допущение косвенного доказательства исключается. Например, осуществим косвенный вывод: (р —> q) ("-(1q —> 1p) (

l.p—>q —посылка

2.1q — допущение

з. Ирдкд

4/Р(3,1и)

5.q(l,4,->„)

6. а л 1я(5,2,лв)

7. 1 Up (6,3, 1в)(-3)

8. 1p (7, 1и)

9. 1q -> 1p (2,8, ->и)(-2)

Косвенный вывод считается законченным, если в ходе вывода получена какая-то формула и ее отрицание, т е. противоречие. Таким образом, если строится косвенный вывод формулы вида xi —> (x-i —>..—> Хп), то построчно выписывают все антецеденты от xi до Xn-i в качестве допущений; в последней строчке выписывают отрицание последнего консеквента — 1хп как допущение косвенного вывода По правилам вывода получаем различные следствия из всех имеющихся посылок и допущений. Получение двух противоречащих следствий говорит о ложности допущения косвен­ного вывода. Па этом основании ДКД отрицается, т.е. получаем двойное отрицание. Снятие двойного отрицания дает формулу Хп.

Основными логическими свойствами системы натурального вывода являются ее непротиворечивость и полнота.

Непротиворечивость означает, что из истинных посылок могут получаться толь­ко истинные следствия и если формула выводима из пустого множества посылок, то она тождественно истинна. Это исключает возможность вывести из пустого множест­ва посылок какую-либо формулу (А) и ее отрицание (1А).

Полнота системы означает, что дедуктивных ее средств достаточно, чтобы вы­вести,из пустого множества посылок любую тождественно истинную формулу.

Логика предикатов является более общей логической системой и включает логику высказываний как свою часть. Она располагает более эффективными логическими средствами для анализа рассуждений в естественном языке.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. На какие виды делятся выводы из сложных суждений?

2. Как строятся чисто условные умозаключения?

3. Что такое условно-категорическое умозаключение? Назовите его правильные модусы, выразите их в символической записи.

4. Какое умозаключение называется разделительно-категорическим? Назовите его модусы, выразите их в символической записи.

5. Укажите условия правильности выводов по утверждающе-отрицающему и от-рицающе-утверждающему модусам разделительно-категорического умозаключения.

6. Какое умозаключение называется условно-разделительным (леммантичес-ким)? Какие модусы имеет дилемма?

7. Что такое энтимема?

8. Каковы принципы построения логики высказываний?

9. Покажите значение различных видов условных и разделительных умозаключе­ний в работе юриста.

Глава VIII ИНДУКТИВНЫЕ УМОЗАКЛЮЧЕНИЯ

Познание в любой области науки и практики начинается с эмпи­рического познания. В процессе наблюдения однотипных природ­ных и социальных явлений фиксируется.внимание на повторяемос­ти у них определенных признаков. Устойчивая повторяемость наво­дит на мысль (индуцирует), что каждый из таких признаков является не индивидуальным, а общим, присущим всем явлениям определен­ного класса. Логический переход от знания об отдельных явлениях к знанию общему совершается в этом случае в форме индуктивного

умозаключения, или индукции (от латинского inductio — «наведе­ние»).

Индуктивным называется умозаключение, в котором на осно­вании принадлежности признака отдельным предметам или час­тям некоторого класса делают вывод о его принадлежности клас­су в целом.

В истории физики, например, опытным путем было установлено, что железные стержни хорошо проводят электричество. Такое же свойство было обнаружено у медных стержней и у серебра. Учиты­вая принадлежность указанных проводников к металлам, было сде­лано индуктивное обобщение, что всем металлам свойственна электропроводность.

Посылками индуктивного умозаключения выступают суждения, в которых фиксируется полученная опытным путем информация о повторяемости признака Р у ряда явлений — Si, 82,.... S„, принадле­жащих одному и тому же классу К. Схема умозаключения имеет следующий вид:

Посылки:

1) Si имеет признак Р S2 имеет признак Р

Sn имеет признак Р 2) Si, 82,..., Sn — элементы (части) класса К

11 - 1У02

Заключение:

Всем предметам класса К присущ признак Р

В основе логического перехода от посылок к заключению в и дуктивном выводе лежит подтверждаемое тысячелетней практикой положение о закономерном развитии мира, всеобщем характере причинной связи, проявлении необходимых признаков явлений через их всеобщность и устойчивую повторяемость. Именно (эти методологические положения оправдывают логическую состоятель­ность и эффективность индуктивных выводов.

Основная функция индуктивных выводов в процессе позна­ния — генерализация, т.е. получение общих суждений. По своему содержанию и познавательному значению эти обобщения могут но­сить различный характер — от простейших обобщений повседнев­ной практики до эмпирических обобщений в науке или универсаль­ных суждений, выражающих всеобщие законы.

История науки показывает, что многие открытия в физике.в области электричества, магнетизма, оптики были сделаны на основе индуктивного обобщения эмпирических данных. Индуктивная обра­ботка результатов наблюдений предшествовала научной классифи­кации растений и животных в биологии. Индуктивным обобщениям обязаны многие гипотезы в современной науке. Важное место при­надлежит индуктивным выводам в судебно-следственной практи­ке — на их основе формулируются многочисленные обобщения, ка­сающиеся обычных отношений между людьми, мотивов и целей совершения противоправных действий, способов совершения пре­ступлений, типичных реакций виновников преступления на дейст­вия следственных органов и т.п.

Полнота и законченность опыта влияют на строгость логическо­го следования в индукции, предопределяя в конечном счете демон-стративность или недемонстративность этих умозаключений.

В зависимости от полноты и законченности эмпирического ис­следования различают два вида индуктивных умозаключений: пол­ную индукцию и неполную индукцию. Рассмотрим их особенности.

§ 1. Полная индукция

Полная индукция — это умозаключение, в котором на основе принадлежности каждому элементу или каждой части класса оп­ределенного признака делают вывод о его принадлежности классу в

целом.

Индуктивные умозаключения такого типа применяются лишь в тех случаях, когда имеют дело с закрытыми классами, число элемен­тов в которых является конечным и легко обозримым. Например,

число государств в Европе, количество промышленных предпри­ятий в данном регионе, число субъектов федерации в данном госу­дарстве и т.п.

Представим, что перед аудиторской комиссией поставлена зада­ча проверить состояние финансовой дисциплины в филиалах кон­кретного банковского объединения. Известно, что в его состав вхо­дят пять отдельных филиалов. Обычный способ проверки в таких случаях — анализ деятельности каждого из пяти банков. Если ока­жется, что ни в одном из них не обнаружено финансовых наруше­ний, то тем самым можно сделать обобщающее заключение: все филиалы банковского объединения соблюдают финансовую дис­циплину.

Схема умозаключения полной индукции имеет следующий вид:

Посылки:

1) Si имеет признак Р §2 имеет признак Р

Sn имеет признак Р 2) Si, 82,..., Sn — составляют класс К

Заключение:

Всем предметам класса К присущ признак Р

Выраженная в посылках этого умозаключения информация о каждом элементе или каждой части класса служит показателем пол­ноты исследования и достаточным основанием для логического переноса признака на весь класс. Тем самым вывод в умозаключении полной индукции носит демонстративный характер. Это означает, что при истинности посылок заключение в выводе будет необходимо истинным.

В одних случаях полная индукция дает утвердительные заключе­ния, если в посылках фиксируется наличие определенного признака у каждого элемента или части класса. В других случаях в качестве заключения может выступать отрицательное суждение, если в по­сылках фиксируется отсутствие определенного признака у всех представителей класса.

Познавательная роль умозаключения полной индукции проявля­ется в формировании нового знания о классе или роде явлений. Логический перенос признака с отдельных предметов на класс в целом не является простым суммированием. Знание о классе или роде — это обобщение, представляющее собой новую ступень в раз-витиизнания.

Так, при выявлении характера кривой, по которой движутся пла­неты вокруг Солнца, в астрономии первоначально было установле­но, что Марс, Венера, Юпитер, Сатурн, Земля обращаются по эллип-сообразным орбитам. С открытием новых планет было установлено, что Уран, Нептун, Плутон и Меркурий обращаются по таким же орбитам. В итоге в форме полной индукции было сделано обобще­ние, что все планеты Солнечной системы обращаются по эллипсооб-разным орбитам. Это новое знание имеет принципиально иное зна­чение, нежели констатация факта эллипсообразного движения каж­дой из планет. Во-первых, обобщающий вывод оказывает влияние на развитие понятия «планета Солнечной системы», поскольку в его содержание может быть включен новый признак — обращение во­круг Солнца эллипсообразное. Во-вторых, этот признак может слу­жить основой для выявления других существенных характеристик всего класса явлений, например, для решения вопроса о механизме возникновения планет Солнечной системы.

Демонстративность полной индукции позволяет использовать этот вид умозаключения в доказательном рассуждении. Так, в гео­метрии теорема о сумме внутренних углов треугольника доказывает­ся отдельно для трех видов треугольников: остроугольных, прямо­угольных и тупоугольных. Учитывая, что в каждом из них сумма углов равна 180° и все они составляют конечное множество, строят индуктивное обобщение: во всяком треугольнике сумма его внут­ренних углов равна 180°.

В судебном исследовании нередко используются доказательные рассуждения в форме полной индукции с отрицательными заключе­ниями. Например, исчерпывающим перечислением разновидностей исключается определенный способ совершения преступления, спо­соб проникновения злоумышленника к месту совершения преступ­ления, тип оружия, которым было нанесено ранение, и т.п.

Применимость полной индукции в рассуждениях определяется практической перечислимостью множества явлений. Если невоз­можно охватить весь класс предметов, то обобщение строится в форме неполной индукции.

Неполная индукция — это умозаключение, в котором на основе принадлежности признака некоторым элементам или частям класса делают вывод о его принадлежности классу в целом.

Схема неполной индукции имеет следующий вид:

Посылки:

1) Si имеет признак Р S2 имеет признак Р

Sn имеет признак Р ' 2) Si, 82, ..., Sn принадлежат классу К

Заключение:

Классу К, по-видимому, присущ признак Р

Неполнота индуктивного обобщения выражается в том, что ис­следуют не все, а лишь некоторые элементы или части класса — от Si до Sn. Логический переход в неполной индукции от некоторых ко всем элементам или частям класса не является произвольным. Он оправдывается эмпирическими основаниями — объективной зави­симостью между всеобщим характером признаков и устойчивой их повторяемостью в опыте для определенного рода явлений. Отсюда широкое использование неполной индукции в практике. Так, напри­мер, во время уборки урожая заключают о засоренности, влажности и других характеристиках большой партии зерна на основе отдельно взятых проб. В производственных условиях по выборочным образ­цам заключают о качестве той или иной массовой продукции, напри­мер, моющих средств — в химической промышленности; труб, ме­таллического листа, проволоки — в прокатном производстве; моло­ка, круп, муки — в пищевой промышленности.

Индуктивный переход от некоторых ко всем не может претендо­вать на логическую необходимость, поскольку повторяемость при­знака может оказаться результатом простого совпадения.

Тем самым для неполной индукции характерно ослабленное ло­гическое следование — истинные посылки обеспечивают получение не достоверного, а лишь проблематичного заключения. При этом обнаружение хотя бы одного случая, противоречащего обобщению, делает индуктивный вывод несостоятельным.

На этом основании неполную индукцию относят к правдоподоб­ным (недемонстративным) умозаключениям. В таких выводах за­ключение следует из истинных посылок с определенной степенью

вероятности, которая может колебаться от маловероятной до^есь-ма правдоподобной.

Существенное влияние на характер логического следования в выводах неполной индукции оказывает способ отбора исходного материала, который проявляется в методичности или систематич­ности формирования посылок индуктивного умозаключения. По способу отбора различают два вида неполной индукции: (1) индук­цию путем перечисления, получившую название популярной индук­ции, и (2) индукцию путем отбора, которую называют научной индукцией.

Популярной индукцией называют обобщение, в котором путем перечисления устанавливают принадлежность признака некото­рым предметам или частям класса и на этой основе проблема­тично заключают о его принадлежности всему классу.

В процессе многовековой деятельности люди наблюдают устой­чивую повторяемость многих явлений. На этой основе возникают обобщения, которые используются для объяснения наступивших и предсказания будущих событий и явлений. Такого рода обобщения бывают связаны с наблюдениями над погодой, влиянием климати­ческих условий на урожай, причинами распространения болезней, поведением людей в определенных ситуациях, отношениями между людьми и т.п. Логический механизм большинства таких обобще­ний — популярная индукция. Ее иногда называют индукцией через простое перечисление.

Повторяемость признаков во многих случаях действительно от­ражает всеобщие свойства явлений. Построенные на ее основе обоб­щения выполняют важную функцию направляющих начал в практи­ческой деятельности людей. Без таких простейших обобщений не­возможен ни один вид трудовой деятельности, будь то совершенст­вование орудий труда, развитие мореплавания, успешное ведение земледелия, контакты между людьми в социальной среде.

В процессе расследования преступлений часто используют эмпи­рические индуктивные обобщения, касающиеся поведения лиц, причастных к преступлению. Например: лица, совершившие пре­ступления, стремятся скрыться от суда и следствия; угроза убийст­вом часто приводится в исполнение; обнаружение похищенных вещей (поличное) свидетельствует о причастности к преступлению. Такие опытные обобщения, или фактические презумпции, как их нередко называют в юридической литературе, часто оказывают не­оценимую помощь следствию несмотря на то, что они являются проблематичными суждениями.

Популярная индукция определяет первые шаги и в развитии научных знаний. Любая наука начинает с эмпирического исследова­ния — наблюдения над соответствующими объектами с целью их описания, классификации, выявления устойчивых связей, отноше­ний и зависимостей. Первые обобщения в науке обязаны простей­шим индуктивным заключениям путем простого перечисления по­вторяющихся признаков. Они выполняют важную эвристическую функцию первоначальных предположений, догадок и гипотетичес­ких объяснений, которые нуждаются в дальнейшей проверке и уточ­нении.

Чисто перечислительное обобщение возникает уже на уровне приспособительно-рефлекторных реакций животных, когда повто­ряющиеся раздражения подкрепляют условный рефлекс. На уровне человеческого сознания повторяющийся признак у однородных яв­лений не просто порождает рефлекс или психологическое чувство ожидания, а наводит на мысль о том, что повторяемость — резуль­тат не чисто случайного стечения обстоятельств, а проявление каких-то невыявленных зависимостей. Обоснованность выводов в популярной индукции определяется главным образом количествен­ным показателем: соотношением исследованного подмножества предметов (образца или выборки) ко всему классу (популяции). Чем ближе исследованный образец ко всему классу, тем основательнее, а значит, и вероятнее будет индуктивное обобщение.

В условиях, когда исследуются лишь некоторые представители класса, не исключается возможность ошибочного обобщения.

Примером этому может служить полученное с помощью попу­лярной индукции и долгое время бытовавшее в Европе обобщение «Все лебеди белые». Оно строилось на основе многочисленных на­блюдений при отсутствии противоречащих случаев. После того как высадившиеся в Австралии в XVII в. европейцы обнаружили черных лебедей, генерализация оказалась опровергнутой.

Ошибочные заключения о выводах популярной индукции могут появиться по причине несоблюдения требований об учете противо­речащих случаев, которые делают обобщение несостоятельным. Так бывает в процессе предварительного расследования, когда решается проблема относимости доказательств, то есть отбора из множест­ва фактических обстоятельств лишь таких, которые, по мнению сле­дователя, имеют отношение к делу. В этом случае руководствуются лишь одной, возможно, наиболее правдоподобной либо наиболее «близкой сердцу» версией и отбирают лишь подтверждающие ее обстоятельства. Другие же факты, и прежде всего противоречащие исходной версии, игнорируются. Нередко их просто не видят и.пото-

му не принимают в расчет. Противоречащие факты также остаются вне поля зрения в силу недостаточной культуры, невнимательности или дефектов наблюдения. В этом случае следователь попадает в плен фактов: из множества явлений фиксирует лишь те, которые оказываются преобладающими в опыте, и строит на их основ/по­спешное обобщение. Под влиянием этой иллюзии в дальнейших на­блюдениях не только не ожидают, но и не допускают возможности появления противоречащих случаев.

Ошибочные индуктивные заключения могут появляться не толь­ко в результате заблуждения, но и при недобросовестном, предвзя­том обобщении, когда сознательно игнорируют или скрывают про­тиворечащие случаи. Такие мнимые индуктивные обобщения ис­пользуются как уловки.

Некорректно построенные индуктивные обобщения нередко лежат в основе различного рода суеверий, невежественных поверий и примет вроде «дурного глаза», «хороших» и «дурных» сновидений, перебежавшей дорогу черной кошки и т.п.

Дата добавления: 2014-12-16