Инструкция 2 страница

В задачах 41—50 систему уравнений записать в матричной форме и решить ее с помощью обратной матрицы:

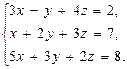
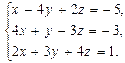
В задачах 51—70 найти указанные пределы (не пользуясь правилом Лопиталя):

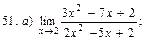
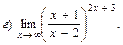
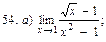
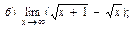
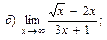
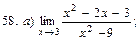
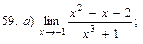
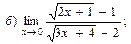
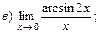
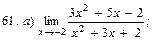
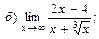
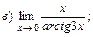
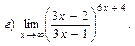
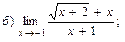
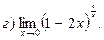
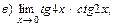
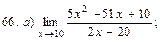
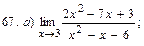
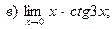
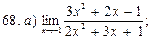
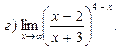
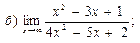
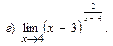
В задачах 71—90 найти производные функций:

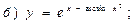
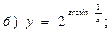
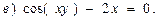
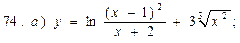
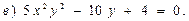
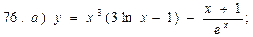
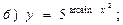
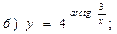
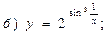
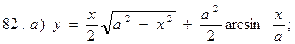
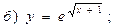
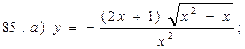
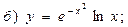
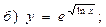
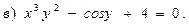
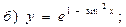
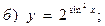
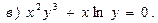
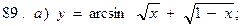
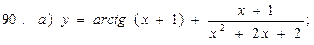
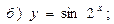
В задачах 91—110 исследовать данные функции метода­ми дифференциального исчисления и построить их графики. Исследование функции рекомендуется проводить по следую­щей схеме: 1) найти область определения функции; 2) иссле­довать функцию на непрерывность; 3) определить, является ли данная функция четной, нечетной; 4) найти интервалы монотонности функции и точки ее экстремума; 5) найти интервалы выпуклости и вогнутости графика функ­ции и точки перегиба; 6) найти асимптоты графика функции:

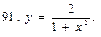
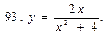
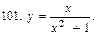
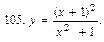
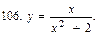
111. Каковы радиус основания R и высота H открытого цилиндрического бака данного объема V, чтобы на его изго­товление пошло наименьшее количество листового металла?

112. Сечение тоннеля имеет форму прямоугольника, за­вершенного сверху полукругом. Периметр сечения 18 м. При каком радиусе полукруга площадь сечения будет наибольшей?

113. Найти стороны прямоугольника наибольшей площади, который можно вписать в эллипс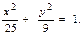

114. Найти наибольший объем цилиндра, полная поверх­ность которого равна S.

115. Найти наибольший объем конуса, образующая кото­рого равна l.

116. Определить размеры открытого бассейна с квадрат­ным дном объемом 32 м³ так, чтобы на облицовку его стен и дна пошло наименьшее количество материала.

117. Сумма двух положительных чисел равна a. Каковы эти числа, если сумма их кубов будет наименьшей?

118. Найти высоту цилиндра наибольшего объема, который можно вписать в шар радиуса R.

119. На параболе y = x² найти точку, наименее удаленную от прямой

y = 2x - 4.

120. Из всех прямоугольников, вписанных в круг радиуса R, найти тот, который имеет наибольшую площадь.

В задачах 121—125 исследовать на экстремум функцию двух переменных:

121. z = 3x + 3y – x² – xy – y² + 6.

122. z = 7x + 8y – x² – xy – y² – 10.

123. z = 8x – 4y + x² – xy + y² + 15.

124. z = x² + y² – 6x – 8y + 12.

125. z = 2x – 8y – x² – y² – 9.

В задачах 126—130 найти наименьшее и наибольшее значения функции двух переменных в данной замкнутой области:

126. z = x² + xy – 6x – 2y + 2 в прямоугольнике 1 £ x £ 3, 1 £ y £ 4.

127. z = x² + 4xy – y² – 5 в треугольнике, ограниченном осями Ох и Оу и прямой у = 2 – х.

128. z = x² + y² – 10x – 2y + 15 в прямоугольнике 2 £ x £ 6, 0 £ y £ 5.

129. z = x² – xy + 8х –y + 7 в области, ограниченной параболой

у = –х² – 4х и осью Ох.

130. z = x² + 2y² + 4xy + 2х + 4y + 2 в квадрате 0 £ x £ 2, 0 £ y £ 2.

В задачах 131—150 найти указанные неопределенные интегралы и результаты интегрирования проверить дифференцированием:

	а	б	в

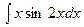
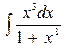
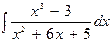
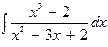
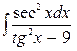
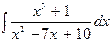
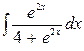
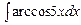
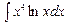
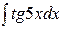
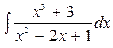
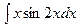
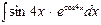
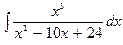
В задачах 151—160 вычислить площадь фигуры, ограни­ченной указанными линиями. Сделать чертеж.

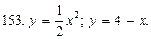
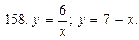
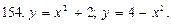
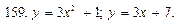
В задачах 161—165 вычислить объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной указанными линиями (сделать чертеж):

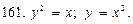
В задачах 166—170 вычислить объем тела, образованно­го вращением вокруг оси Оу фигуры, ограниченной указанными линиями (сделать чертеж):

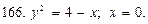
В задачах 171—190 найти общее решение дифференциаль­ных уравнений первого порядка:

а) с разделяющимися переменными:

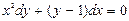
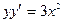
б) линейные:

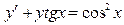
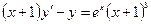
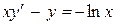
В задачах 191—200 найти частное решение дифференци­ального уравнения второго порядка, удовлетворяющее ука­занным начальным условиям:

.

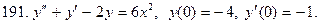
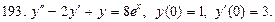
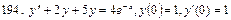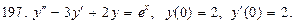
В задачах 201—220 дан степенной ряд. Найти интервал сходимости ряда и исследовать его сходимость на концах интервала:

201. . 202. .

Дата добавления: 2014-12-16