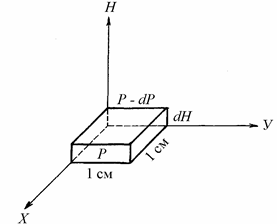
Изменение атмосф ерного давления с высотой

Атмосферное давление убывает с вы сотой, поскольку масса выш ележащего ст олба воздух а уменьшается. Для определения общ его закона изменения давления с высото й возьмем систему координат с осью Н, направленной вертикально вверх. Представим, что на плоскости ХУ давление воздуха равно Р. Выделим элемент арный объем с сечением, равным

1 см2, и высотой dH (рис. 2.7). Давление на верхней грани объема будет р авно P - dP.

Величина изменения давления dP равна весу возд уха, заключенного в рассматриваемом объеме (r dН – масса, r gdН – вес).

где: r - плотность возд уха;

 

g -ускорение силы т яжест и.

dP = -r gdH

(2.19)

Р ис. 2.7. Изменение давления с в ысотой

Полученное уравнение называется основным уравнением статики атмосферы. Знак минус в правой части показывает, что величина dP отрицат ельная, т.е. давление с высотой уменьшается. Проинтегрируем данное уравнение. Для эт ого подставим в него величину плотности воздуха из уравнения состояния газов

(PV =

RT,

V = 1,

r

P = r RT,

r= P) и пол учим

RT

где: Р – давление воздуха;

R - газовая постоянная;

Т -аб солютная т емпература.

dP =- gP dH, (2.20)

RT

Разделим переменные и проинтегрируем левую часть от Р 0 до Рн, а правую ч асть - от

0 д о Н:

Pн dP

ò

Н

=ò-

g

dH. (2.21)

P 0 P

0 RT

Так как g и R изменяются незначительно, то их можно счит ать постоянными.

Температура возд уха с высот ой изменяет ся, поэ тому возьмем ее среднюю величину Тср в

Т 0 + Тн

слое от 0 до Н (Т ср =

2) и также б удем счит ать ее постоянной величиной. После этого

выражение (2.22) примет вид:

Pн dP

ò

dH

g Н

=- ò. (2.22)

В результате интегрирования получим:

P 0 P

RTср 0

gH

ln Pн

-ln P 0 =-

RТср

+0. (2.23)

От сюда:

ln Pн

=ln P 0

- gH.

RТср

Умножив второй член правой части на ln e = 1, получим:

ln P н

=ln P 0

- gH ln е.

RТср

После потенцирования имеем:

- gH

Pн

= P 0

gH

e RTср

или

Pн = P 0 e

RTс р

, (2.24)

где: Р 0 - давление на нижнем уровне;

Рн -давление на высот е Н;

е - осно вание нат уральных логарифмов.

Получ енная фор мула (2.24) вы ражает общ ий за кон изм енения да вл ения с высотой, кот ор ый показывает, чт о с высотой давление уменьшается по логарифмическому закону: в нижних слоях атмосферы оно уменьшается быстрее, чем в верхних.

Дата добавления: 2014-12-16