Ю.И. Категоренко 5 страница

В результате поверхностного проникновения металла в поры смеси на поверхности отливки образуется и удерживается после выбивки более или менее толстый слой пропитанной металлом формовочной смеси, иногда очень трудноудалимый. Этот поверх­ностный дефект отливок называют пригаром. Пригар, образуемый по описанному механизму, называется механическим пригаром.

Однако на практике чисто механический пригар образуется редко. В условиях окислительной атмосферы формы поверхность металла часто покрыта пленками окислов. Например, при литье железоуглеродистых сплавов важную роль играют окислы железа и марганца FeO и МпО. С кремнеземом песка эти окислы всту­пают во взаимодействие с образова­нием легкоплавких соединений типа файялита (2FeO×SiO₂), родонита (MnO×SiO₂), тефроита (2MnO×Si0₂) и др. С возникновением окисных или силикатных легкоплавких фаз про­никновение сплава в поры смеси су­щественно облегчается. Окислы хоро­шо смачивают смесь и сами хорошо смачиваются металлом. Расплав идет за ними в капилляр как нитка за иголкой. Следует заметить, что окисные расплавы легко пропитывают по­верхностный слой смеси, химически разрушая зерна песка. Иногда вме­сто зерен песка в пригарном слое об­наруживают монолитную массу, со­стоящую из указанных выше соеди­нений. При этом образуется наиболее тяжелый вид пригара — химический. Из изложенного следует, что необходимой стадией химического пригара являются процессы, связанные с механическим пригаром. Схема образования пригарного слоя показана на рис. 1.41. К описанным выше процессам следует добавить процессы плавления наиболее легкоплавких составляющих смеси (окислы щелочных металлов, зерна поле­вого шпата, алюмосиликаты глины и т. п.) и их последующего спекания. Эти процессы характерны для так называемого терми­ческого пригара.

Все указанные виды пригара, как правило, сосуществуют. Пригарный слой представляет собой самостоятельную фазу, име­ющую свою структуру. Этот слой удерживается на поверхности отливки не только за счет действия проникших в смесь прожилок металла, но и за счет адгезии, чему способствуют спекание слоя и структурные превращения в нем. Для уменьшения адгезии не­обходимо повысить межфазное натяжение на границе поверхность отливки — пригарный слой. В тех случаях, когда межфазное натя­жение на этой границе мало, что имеет место при близких струк­турах металла и слоя, пригарный слой прочно удерживается на поверхности отливки силами адгезии.

Для примера можно привести неожиданный результат, полученный при освоении жидкостекольных смесей на УЗТМ в начале 50-х гг. Данные смеси, связующим в которых является силикат натрия или калия, содержат большое количество легкоплавких окислов щелочных металлов и поэтому отличаются большой пригораемостью. К удивлению технологов, смеси относительно легко были внедрены на стальном литье. При этом образовывался до­статочно толстый слой пригара, который легко отскакивал от поверхности отливок при их очистке. В то же время на чугунном литье, несмотря на значительно меньшую, чем при стальном литье, температуру заливки, при применении жидкостекольных смесей образуется трудноудалимый от поверхности отливки пригарный слой. Минералогический и рентгеноструктурный анализ пригарного слоя показали, что при температурах, характерных' для литья чугуна, он имеет кристаллическую структуру, близкую к структуре металла. Это приводит к снижению межфазного натя­жения на границе отливка — пригарный слой и, как следствие, к увеличению адгезии. При литье стали пригарный слой имеет вид аморфно-стекловидной массы, что приводит к увеличению межфазного натяжения и снижению адгезии.

Таким образом, поверхностные явления играют важную роль в пригарообразовании. Естественно, такой сложный процесс не исчерпывается только поверхностными явлениями. Комплексное рассмотрение пригарообразования — предмет технологических раз­делов спецкурса. С точки же зрения поверхностных явлений борь­ба с пригаром должна быть направлена на уменьшение как смачиваемости металлом материала формы, так и адгезии слоя к сплаву. Это может достигаться соответствующим подбором формо­вочных материалов, противопригарных покрытий, раскислением металла, предотвращением его окисления в форме, соответствую­щим легированием сплава и т. п.

Рассмотренные свойства жидких металлов и сплавов не охва­тывают всех их важнейших технологических характеристик. Мы не рассматривали механические свойства сплавов в жидком и двух­фазном состояниях, теплоемкость жидких сплавов и их тепло­проводность и другие свойства. Эти свойства металлов и сплавов будут рассмотрены в соответствующих разделах курса.

КОНТРОЛЬНЫЕ ВОПРОСЫ И УПРАЖНЕНИЯ

1. Что такое ближний и дальний порядок?

2. Какова основная причина плавления твердых тел?

3. Особенности теплового движения твердых, жидких и газо­образных тел.

4. В чем причина объемного расширения тел в твердом со­стоянии?

5. Объемные изменения при плавлении тел.

6. Что такое радиальная функция распределения и корреля­ционная функция?

7. Каков смысл и вид радиальной функции распределения и корреляционной функции для газов, жидкостей и твердых тел?

8. Что такое кластер?

9. Зависимость вязкости металлов и сплавов от состава, тем­пературы и давления.

10. Что такое реология?

11. Модель и поведение H -тела и N -тела.

12. Модель и поведение B -тела.

13. Модель и поведение сплава в интервале ликвидус — солидус,

14. Что такое адгезия и когезия?

15. Механизмы образования пригара.

16. Меры борьбы с пригаром.

17. Формулы для вычисления величины капиллярного давле­ния.

18. Рассчитать температуру плавления алюминиевого шарика диаметром 0,0001 мм при следующих параметрах: равновесная температура плавления при плоской границе фаз Т_равн = 660°С; поверхностное натяжение (s_т-ж = 860×10^-3 Дж/м²; теплота плавле­ния L = 418 кДж/кг; плотность r = 2710 кг/м³.

19. Найти координационное число для компактной гексагональной решетки.

20. Найти радиусы четырех первых координационных сфер для компактной гексагональной решетки и построить для нее график распределения числа атомов по координационным сфе­рам.

21. Определить величину относительной деформации H -тела при сдвиге, если t = 300 МПа, E = 70 ГПа, m = 0,31.

22. Вывести формулу Пуазейля для вычисления средней ско­рости и расхода ньютоновской жидкости в цилиндрическом кана­ле радиусом R при постоянном перепаде давлений ΔР. Во сколь­ко раз возрастет расход, если радиус канала увеличить в 2 раза?

23. Построить график изменения деформации B -тела во вре­мени при следующих исходных данных: t = 100 Mпа = const, t_s = 60 МПа, h = 10 Н×с/м², G = 1 ГПа. Какой будет деформация через 30 с?

24. Вычислить вязкость алюминиевого сплава, содержащего в 1 см³ 2000 частиц радиусом 0,1 см, если вязкость чистого спла­ва h₀ = 10^-2 Н×с/м².

25. Построить график изменения деформации тела Кельвина при t = 300 МПа, G = 1 ГПа, h = 10 Н×с/м². Какой будет дефор­мация через 30 с? По какой кривой идет уменьшение деформации при разгрузке?

Раздел 2. ОСНОВЫ ТЕОРИИ ФОРМИРОВАНИЯ КРИСТАЛЛИЧЕСКОЙ СТРУКТУРЫ ОТЛИВОК

Среди литейных процессов центральное место занимает пере­ход сплава из жидкого в твердое кристаллическое состояние. Этот процесс является фазовым переходом первого рода, связанным с изменением объема, теплосодержания и энтропии. При рассмот­рении данного процесса можно выделить два аспекта: количест­венный и качественный. Количественный аспект составляет содер­жание теории затвердевания, главной задачей которой является разработка методов расчета кинетики выделения твердой фазы в объеме расплава. Качественный аспект направлен на рассмот­рение вопросов формирования кристаллической структуры отли­вок и методов управления ею.

ГЛАВА 2.1. ОСНОВНЫЕ ЗАКОНОМЕРНОСТИ САМОПРОИЗВОЛЬНОЙ КРИСТАЛЛИЗАЦИИ МЕТАЛЛОВ И СПЛАВОВ

Современная теория формирования кристаллической структуры отливок.создана за последние 20 лет на основе творческого рас­пространения элементарной теории кристаллизации металлов и сплавов на большие объемы неизотермически затвердевающих расплавов.

Жидкий металл переходит в твердое состояние в соответствии с общими законами термодинамики. Как известно, самопроиз­вольно протекают те процессы, в которых уменьшается свободная энергия и энергия Гиббса G. На рис. 2.1 приведены кривые изменения энергии Гиббса твердого и жидкого металла в зависи­мости от изменения температуры. Видно, что при температуре, большей Т_пл, G_ж < G_тв и устойчивым является жидкое состояние металла. При T < T_пл G_тв < G_ж, поэтому устойчивым является твердое состояние. Температура Т = T_пл, при которой G_тв = G_ж, называется температурой плавления. При равновесном процессе перехода из жидкого состояния в твердое эта температура соот­ветствует равновесной температуре кристаллизации сплава T_кр. "При снижении температуры ниже Т_кр возникает переохлаждение Δ T = T_кр — Т. Так как при этом G_ж > G_тв, то создаются термоди­намические предпосылки для перехода из жидкого состояния в твердое, т. е. для кристаллизации. Движущей силой этого процесса будет разность энергий Гиббса Δ G = G_ж — G_тв. Преобразу­ем это выражение, прибавив и отняв энергии Гиббса жидкой и твердой фаз при T = Т_кр.

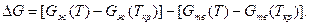
Так как G_ж(Т_кp) = G_тв(Т_кр), то равенство при этой операции не нарушится. Поскольку реальные переохлаждения металлов не ­ велики, то для стоящих в квадратных скобках выра-

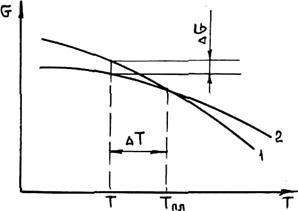
Рис. 2.1. Зависимость энергии Гиббса жидкого (/) и твердого (2) металла от температуры

жений можно написать следующие приближенные равенства:

,

.

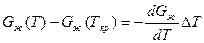С учетом этого Δ G = — Δ Т(dG_ж/dТ — dG_тв/dТ). Так как dG/dТ = —S, то Δ G = + Δ T×ΔS, где Δ S — изменение энтропии при плавлении металла. Как известно, Δ S = L/T_пл, где L— молярная теплота плавления, следовательно, Δ G = L×ΔT/Г_кр. Из этого вы­ражения видно, что с ростом переохлаждения движущая сила кристаллизации увеличивается.

Следует отметить, что при кристаллизации возникает новая фаза, имеющая физическую поверхность раздела с жидкостью. Поэтому кристаллизация связана с затратами энергии на обра­зование и рост данной поверхности раздела фаз. Величина этой энергии равна E_s = s_к-ж×S, где s_к-ж — межфазная энергия на границе раздела фаз; S — поверхность растущего кристалла. В результате образования кристалла объемом V с поверхностью S энергия системы уменьшится на величину Δ G_v и увеличится на величину E_s. Поэтому изменение суммарной энергии Гиббса бу­дет равно

,

где r и М— плотность твердого металла и его молярная масса. Анализ характера зависимости Δ G_å от объема кристалла V пока­зывает, что она имеет экстремальный характер. Характер зависи­мостиΔ G_å от радиуса зародыша показан на рис. 2.2.

Кис. 2.2. Зависимость Δ G_å от радиуса зародыша r при разных температурах (T₁>T₂>T_кр>Т₃>Т₄)

В курсе металловедения получено следующее выражение для критического размера сферического зародыша, обеспечивающего максимум Δ G_å (читателю предлагается вывести его самостоя­тельно):

.

Из рис. 2.2 видно, что с понижением температуры, т. е. с уве­личением переохлаждения, радиус критического зародыша стано­вится меньше (r_кр2 < r_кр1). При этом уменьшается и энергия образования критического зародыша.

,

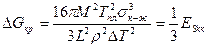где E_sкр — поверхностная энергия зародыша критических размеров.

Пусть по каким-либо причинам в расплаве при данном пере­охлаждении возник зародыш радиуса r < r_кр. Рост такого зародыша (увеличение r), как видно из рис. 2.2, сопровождается рос­том Δ G_å. Поэтому данный зародыш не способен к росту и будет расплавляться. Если радиус зародыша r ³ r_кр, то при присоеди­нении к нему даже одного атома, т. е. с ростом его размеров, Δ G_å будет убывать. Поэтому данный зародыш сможет расти.

Центром кристаллизации будет называться зародыш, обяза­тельно способный к росту. Критический зародыш (r = r_кр) еще не является центром кристаллизации: он может потерять хотя бы одну частицу, т. е. стать дозародышем (r < r_кр) и исчезнуть, или

Рис. 2.3. Зависимость вероятности Р₁ флуктуации энергии Е от величины флуктуационного отклонения Δ Е

присоединить хотя бы одну частицу (r > r_кр) и получить возмож­ность для роста, т. е. стать центром кристаллизации. Поэтому вероятность образования центра кристаллизации равна произве­дению вероятностей образования зародыша критических разме­ров p₁ и присоединения к нему частицы р₂, т. е. p = p₁× p₂.

Вероятность образования центра кристаллизации равна отно­шению числа возникших в единицу времени в единице объема расплава центров кристаллизации п к общему числу частиц в расплаве N, т. е. p = n/N. Величина п, называемая скоростью воз­никновения центров кристаллизации (СВЦК), является важней­шей кристаллизационной характеристикой металлического рас­плава. Очевидно, n = p× N = p₁× p₂× N. Размерность [п] — м^-3× c^-1.

Для того чтобы определить вероятность p₁, рассмотрим вопрос о причинах появления зародышей в условиях возрастания сум­марной энергии Гиббса Δ G_å. С точки зрения статистической фи­зики характерные для равновесия значения термодинамических величин представляют собой лишь наиболее их вероятные при данных условиях значения. Практически отдельные микрообъемы жидкости в течение некоторых малых промежутков времени мо­гут обладать значениями термодинамических величин, отличными от отвечающих данному равновесному состоянию. При этом боль­шую часть времени система обладает равновесными термодинами­ческими характеристиками. Случайные отклонения какой-либо величины от ее равновесного значения называются флуктуациями. Вероятность обнаружения флуктуации зависит от ее величины. Чем больше флуктуация, т. е. отклонение от соответствующего равновесного значения, тем она менее вероятна и тем меньшее время система обладает соответствующим отличным от равновес­ного значением той или иной величины. Следует отметить, что кривая зависимости вероятности флуктуации от ее величины отли­чается острым максимумом в области нулевых флуктуаций (рис. 2.3). Поэтому с увеличением флуктуации вероятность ее появления резко снижается до нуля.

Благодаря наличию флуктуации энергии в расплаве будет находиться то или иное количество микрообъемов, обладающее избытком энергии, необходимым для совершения работы образо­вания зародыша критических размеров Δ G_кр. Вероятность такой энергетической флуктуации равна p_l = n_к/N = exp(— Δ G_кр/kТ), где n_к — число зародышей критического размера; N— общее число частиц в единице объема. Вероятность p₁ и будет вероятностью возникновения зародыша критического размера в единице объема в единицу времени. Очевидно, что, чем больше Δ G_кр, тем боль­шая требуется энергетическая флуктуация и меньше вероятность р₁. Так как с увеличением переохлаждения Δ T Δ G_кр уменьшается, то с ростом Δ Т повышается р₁. Вероятность присоединения к за­родышу хотя бы одной частицы равна p₂ = n_sen× exp(—U/kT), где n _s— число атомов в жидкости, находящихся в контакте с поверх­ностью зародыша; e = l/6 — вероятность скачка атомов в данном направлении; n — частота колебаний атомов в жидкости (n = 10¹³•c^-l); U— энергия активации диффузии атомов в жидкости, определяющая подвижность атомов.

Таким образом, вероятность образования центра кристаллиза­ции равна

. (2.1)

С учетом формулы (2.1) для вычисления скорости возникновения центров кристаллизации можно записать выражение

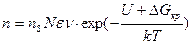. (2.2)

С увеличением переохлаждения Δ G_кр уменьшается, а U воз­растает (снижается подвижность атомов). Поэтому зависимость п от Δ Т носит экстремальный характер (рис. 2.4). Подобную кривую получил впервые в начале века Г. А. Тамман при кристал­лизации органических прозрачных жидкостей. Для чистых гомо­генных металлических расплавов зависимость п от Δ T показана на рис. 2.5. Видно, что при переохлаждениях, меньших величины Δ Т₁, называемой интервалом метастабильности по зарождению, зарождение центров кристаллизации практически не происходит. Для металлов ниспадающая ветвь кривой (см. рис. 2.4) не реа­лизуется, так как подвижность атомов в металлах очень велика.

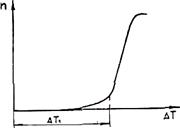
Рис. 2.4. Зависимость СВЦК " от переохлаждения ΔТ Рис. 2.5. Зависимость СВЦК от пере­охлаждения

для очистки гомогенных металлических расплавов

Для чистых гомогенных металлических расплавов величина интервала метастабильности очень велика. Расчеты показывают, что Δ T₁» 0,2 Т_кр. Реально подобная переохлаждаемость распла­вов не наблюдается, так как в расплаве всегда находится доста­точное количество примесей, инициирующих зародышеобразование.

Обычно самопроизвольную гомогенную кристаллизацию изу­чают на мельчайших каплях чистого металла. При этом считает­ся, что при измельчении металла вероятность нахождения при­меси в капле уменьшается. Зависимость n от Δ T для металлов можно аппроксимировать следующей степенной зависимостью: n = n₀(ΔT — ΔT₁)^s, где показатель степени s находится в интер­вале от 1 до 3.

Выше речь шла о самопроизвольном зарождении кристаллов при затвердевании однокомпонентных расплавов (чистых ме­таллов). Большинство литейных расплавов являются сплавами, т. е. высокотемпературными жидкими растворами. При этом про­дуктами кристаллизации чаще всего являются твердые растворы. При охлаждении до температуры ликвидуса жидкий сплав ока­зывается насыщенным по отношению к легирующему компоненту. Поэтому при дальнейшем снижении температуры наступает пересыщение и из расплава должны выделяться твердые кристаллы.

Свойства, не зависящие от количества вещества, называются интенсивными. К ним относятся температура и давление. При­менительно к растворам Г. Н. Льюис ввел еще одну интенсивную величину, называемую парциально-молярной величиной компо­нента. Она представляет собой частную производную от какого-либо экстенсивного свойства W по числу молей этого компонента при постоянных давлении, температуре и числе молей остальных компонентов в растворе, т. е. q_i = (дW/дn_i}_{p,T,n j¹i} Например, парциально-молярная энергия Гиббса для (i -го компонента равна G_i = (дG/дп_i)_{р,T, j¹i}. Легко понять, что парциально-молярные свойства чистых веществ совпадают со значением этих свойств одного моля

Рис. 2.6. Схема графического определения состава фаз, находящихся в равновесии при заданной температуре

вещества для заданных условий (G⁰A и G⁰B). Дейст­вительно, для вещества A G = nG⁰_A и дG/дп = G⁰_A. Величина дG/дп_i называется химическим потенциалом m_i, т. е. m_I = (дG/дп_i)_{P,T, j¹i} Химический потенциал характеризует тенден­цию вещества покинуть данную фазу и перейти в другую. Физи­чески химический потенциал равен работе, которую нужно со­вершить, присоединяя к раствору одну частицу данного компо­нента. Интенсивные величины Т, Р и m_I характеризуют условия термического, механического и химического равновесия. Для рав­новесия необходимо, чтобы во всех фазах были одинаковые тем­пературы, давления и химические потенциалы компонентов.

Приравняв величины m_I для каждого компонента во всех фа­зах, получим систему уравнений, которая совместно с уравнениями материального баланса позволяет найти составы находящихся в равновесии фаз. Для двойных сплавов этот подход хорошо реализуется графически. На рис. 2.6 показан пример графическо­го метода определения состава твердого раствора и находящейся с ним в равновесии при некоторой температуре Т жидкой фазы. При равновесии должны выполняться условия m^тв_А = m^ж_А и m^тв_В = m^ж_В, а если m_В = дG/дп_в, то составы фаз должны обеспечивать выполнение равенства

или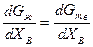

Геометрически это означает, что составы определяются общей касательной к кривым зависимости энергий Гиббса твердой и жидкой фаз при данной температуре. Эти равновесные составы G^тв_В и G^ж_В показаны на рис. 2.6. Иногда считают, что искомые составы отвечают точкам пересечения кривых мольных энергий фаз, например точке А, т. е. точкам, где равны энергии фаз. Од­нако равновесные фазы обеспечивают минимум суммарной энер­гии обеих фаз, а он достигается только при m^ж_А = m^тв_А и m^ж_В = m^тв_В.

Таким образом, при достижении пересыщения из раствора могут выделяться твердые растворы, концентрации которых от­личаются от исходной. При этом для начала процесса кристал­лизации необходимо пересыщение раствора, достигаемое его пере­охлаждением относительно температуры ликвидуса.

Движущая сила, создающая условия для выделения твердой фазы в сплавах, определяется так же, как и для металлов, по изменению энергии Гиббса системы.

При кристаллизации сплавов вместо справедливого для одно­компонентного металла выражения Δ G^м = L× Δ T'/T_пл следует при­менять выражение Δ G_ж-a С учетом этого для критического размера зародыша получим выражение r_кр = 2sМ/(r× Δ G^м_ж-а). Работа образования критического сферического зародыша равна 16 pМ²s³/[ З r²( Δ G_ж-а)²].

Следует отметить, что зарождение центров кристаллизации сплавов, как показали исследования, качественно описывается той же зависимостью от переохлаждения, что и у металлов. При этом переохлаждение отсчитывается от температуры ликвидуса. Величину Δ G^м_ж-a можно также вычислить по формуле L Δ T/Т_л, где L — теплота кристаллизации, выделившаяся при кристалли­зации единицы массы сплава при данной температуре.

Для образования зародышей твердых растворов необходимы не только рассмотренные выше энергетические флуктуации, но и флуктуации концентрации. Концентрационные флуктуации пред­ставляют собой участки растворов, состав которых отличается от среднего. Например, в жидком чугуне при средней концентрации углерода 3,4 % обнаруживаются участки размером 10^-8 см, состоящие из одного углерода. По-видимому, именно эти участки являются основой возникновения зародышей графита при кристал­лизации чугуна.

Рассмотренный выше процесс кристаллизации сплавов назы­вается диффузионным, так как при кристаллизации в этих слу­чаях происходит перераспределение компонентов между фазами путем диффузии.

Рис. 2.7. Схема бездиффузион­ной кристаллизации

Возможен бездиффузионный про­цесс кристаллизации сплавов, когда состав выделяющейся твердой фазы строго совпадает с составом исход­ного жидкого сплава. На рис. 2.7 представлена диаграмма состояния и зависимость G от состава для жид­кого сплава и сплава в твердом со­стоянии. Зависимость G приведена при T = T₁. Точка A` отвечает равен­ству мольных энергий Гиббса твер­дой и жидкой фаз. На диаграмме состояния ей соответствует точка А`. Если аналогичные точки перенести на диаграмму при других температурах, то получим линию EF, отвечающую равенству G_т = G_ж. Если сплав рез­ко переохладить ниже этой линии (например до T = T₂), то G_т станет меньше G_ж и произойдет бездиффу­зионная кристаллизация с выделени­ем твердой фазы концентрации С₀. Анализ показывает, что для этого нужны очень большие пере­охлаждения (порядка нескольких десятков и даже сотен.граду­сов) В обычной литейной практике они не достигаются, так как требуют очень больших скоростей охлаждения при малых объ­емах сплава.

ГЛАВА 2.2. ТЕОРИЯ ГЕТЕРОГЕННОГО ЗАРОДЫШЕОБРАЗОВАНИЯ

Большинство металлов затвердевает при значительно меньшем переохлаждении, чем максимальное переохлаждение Δ T_mах = 0,2T_кр предсказываемое теорией гомогенного образования за­родышей. Это обусловлено наличием в расплаве инородных твер­дых частиц которые облегчают возникновение зародышей, Рас­смотрим простейший случай образования зародыша на плоской поверхности включения.

Пусть зародыш ограничен частью сферической поверхности радиуса R (рис. 2.8). Изменение полной мольной энергии сплава при образовании зародыша в данном случае имеет вид

,

где s_2-3 и s_1-2 — межфазные энергии на границах сплав — за­родыш и зародыш — включение; w_сф и w_вкл — площади поверхностей зародыша на границе со сплавом и на границе с включе­нием; s_1-3 — межфазная энергия на границе между включением и сплавом. Выполнив геометрические преобразования (предлага­ем читателю выполнить их самостоятельно), получаем следующие формулы для вычисления V, w_сф и w_вкл:

;

; .

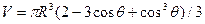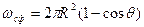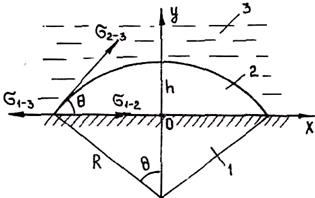
Рис. 2.8. Схема зарождения кристалла на плоской по­верхности включения:

/ — включение; 2 — зародыш; 3 — сплав

Подставив эти выражения в формулу для Δ G_å и выполнив исследования на максимум, получаем следующие выражения для вычисления энергии образования критического зародыша на вклю­чении и соответствующего ему размера R_кр:

Дата добавления: 2014-12-16