Как язык науки 1 страница

ОСНОВАНИЯ МАТЕМАТИКИ

Мальчики играют на горе,

Сотни тысяч лет играют.

Царства исчезают на Земле,

Игры — никогда не умирают.

Искусственные миры и математика. Почему человечество создало математику? Почему математика устроена аксиоматически? О единстве и целостности математики. Математика и геометрия. Устройство математических теорий. Отличие математического языка от естественного. Интерпретация математических теорий. Почему ЗНАНИЕ математики не гарантирует УМЕHИЯ ей пользоваться в конкретном проектировании систем? Классификатор возможных задач. Введение системы координат. Правило записи алгоритма. Точечное преобразование и преобразование координат. Инварианты, системы координат и «точки зрения». Ум — измерение — наука. Геометрия и хронометрия. Единицы измерения пространства и времени. Какова «ключевая идея», которая приблизила нас к современному уровню понимания математики? Множественность геометрий и множественность классов явлений природы. Исходные правильные формулы как противоречие. Интегрирующий принцип — тензорные преобразования с инвариантом.

1. Искусственные миры и математика

Бренность человеческой жизни и мечта о бессмертии — рождают странные миры: мир мифов, мир сказок, мир художественной литературы, мир музыки и т.п., которые можно назвать МИРАМИ ИСКУССТВА или ИСКУССТВЕННЫМИ МИРАМИ. К числу таких искусственных миров и принадлежит мир математики. Каждый из искусственных миров НЕОБХОДИМ ЧЕЛОВЕЧЕСТВУ, но остается неясным: «Почему человечество должно было ПРИДУМАТЬ эти миры и какую роль в истории человечества играют эти миры?»

Мы полагаем, что ответ на вопрос о возникновении подобного искусственного мира, известного как МИР МАТЕМАТИКИ, не может быть получен без ответа на более ОБЩИЙ ВОПРОС об искусственных мирах В ЦЕЛОМ.

Если миры искусства весьма уважают чувство юмора, то только отсутствие этого чувства в большинстве «математических» работ лишает их того очарования, которое традиционно связано с каждым миром искусства.

Яростная дискуссия об основаниях математики, противостояние математических школ, лишает эту область ТВОРЧЕСТВА заслуженного внимания к этим проблемам. Само собою разумеется, что только отсутствие чувства юмора не позволяет с шуткой на устах обсуждать проблему НЕПРОТИВОРЕЧИВОСТИ математических теорий. Здесь как в тюрьме — «вологодский конвой шутить не любит: шаг вправо, шаг влево считается за побег — конвой применяет оружие без предупреждения!» И совсем не случайно участие математиков в различных «правозащитных движениях».

То, что мы пытаемся обсудить в этом разделе, уже давно известно как литературный прием, названный Шкловским «ОСТРАНЕНИЕ», что можно понимать как «остраненный взгляд» или «взгляд со стороны».

Два тысячелетия мы храним художественное наследие древних греков и столько же времени мы храним их наследие из мира математики. Уже архитектурные формы, созданные из камня, не выдерживают испытания текущим временем, а греческие тексты — как из мира искусства, так и из мира математики — оказались поистине НЕТЛЕННЫМИ. Но именно там, два тысячелетия тому назад, мы встречаемся в объектом, на который не действует ДЕЙСТВИТЕЛЬНОЕ ВРЕМЯ — это мир ИДЕЙ в том смысле, как их понимал Платон. И математика чтит эту традицию, сохраняя за одним из своих созданий имя «платоновых тел». Нет Платона, но живут и будут жить вечно — «платоновы тела»!

Из обилия возможных проблем мы выбираем только три:

Почему человечество (с необходимостью, присущей случаю) должно было придумать математику?

Почему математика должна быть устроена аксиоматически?

Почему ЗНАНИЕ математики не гарантирует УМЕHИЯ ей пользоваться в конкретном проектировании систем?

2. Почему человечество создало математику?

Хотя придуманных миров довольно много, мы стоим перед необходимостью выделить из этого РОДА тот ВИД, который и именуется математикой. Это мир «идеальных объектов», которые обладают уникальным свойством — они «остаются тождественными САМИ СЕБЕ». В этом смысле на объекты математики НЕ ДЕЙСТВУЕТ ВРЕМЯ, они обладают как бы «вневременным бытием».

Такие объекты, как прямая линия, квадрат, окружность и т.д. не могут быть «физически изготовлены», все они «чистые произведения мысли», но отличаются от всех других произведений мысли именно своей тождественностью самим себе. Нелепая попытка некоторых физиков отождествлять «прямую линию» с траекторией солнечного луча опровергается каждым школьником, который знает эффект рефракции и знает, что солнечный луч при закате «загибается». Это отклонение солнечного луча от математической «прямой линии» означает, что «прямая» в сознании школьника математичнее, чем у некоторых физиков.

А.Пуанкаре полагал, что первой математической абстракцией является абстракция «абсолютно твердого тела», а «прямая линия» может быть определена не проще, чем через «ось вращения абсолютно твердого тела».

Этот мир неизменных объектов, тождественных самим себе, в форме циклов и эпициклов послужил Птолемею для ПРЕДСКАЗАНИЯ Солнечных и Лунных затмений, а также для ПРЕДСКАЗАНИЯ моментов весеннего и осеннего равноденствий, знание которых давало возможность ПРЕДСКАЗАВАТЬ разлив Нила. Связь «математического мира» и наблюдаемых явлений природы породила профессию ЖРЕЦОВ, которые и являются подлинными прародителями современной математики.

Когда на историческом горизонте возникает фигура Кеплера, то не только изменяется «картина мира», но траектории планет ОТОЖДЕСТВЛЯЮТСЯ с эллипсом планетной орбиты. Этот НЕИЗМЕННЫЙ ЭЛЛИПС — и есть ПЕРВЫЙ закон ПРИРОДЫ, зафиксированный на первых шагах науки нового времени. Здесь мы видим, что если НЕЧТО, наблюдаемое в природе, мы можем ОТОЖДЕСТВИТЬ с некоторым объектом математики, то этот математический объект явится ПРАВИЛОМ, на которое не действует ВРЕМЯ. Но такое свойство и есть то, что мы с этого времени будем называть ЗАКОНОМ ПРИРОДЫ.

Есть большая правда в том, что природа говорит с нами на «языке математики», но не надо забывать, что ЗАКОНЫ НЕБЕСНОЙ МЕХАНИКИ не есть математические символы, изображенные на небесном своде. Создание мира неизменных объектов впервые позволило человечеству освоить понятие «ЗАКОНА ПРИРОДЫ», как чего-то такого, что СУЩЕСТВУЕТ как не подверженное ходу действительного ВРЕМЕНИ.

Так человечество встретилось с «писанием ЗАКОНОВ». Но нетрудно заметить разницу между законами Кеплера и законами юристов, которые считаются большими мастерами по «писанию законов». Один из наших оппонентов, более четверти века тому назад, утверждал, что законы издает Верховный Совет СССР. А когда его спросили: «Не может ли Верховный Совет СССР отменить, например, законы Ньютона?» — оппонент пришел в замешательство. Мы не можем отказать себе в удовольствии процитировать Гегеля, ярко обрисовавшего подобных борзописцев:

«Можно при этом отметить особую форму нечистой совести, проявляющуюся в том виде красноречия, которым кичится эта поверхностность; причем прежде всего она сказывается в том, что там, где в ней более всего ОТСУТСТВУЕТ ДУХ, она более всего говорит о ДУХЕ; там, где она наиболее МЕРТВЕННА и СУХА, она чаще всего употребляет слова ЖИЗНЬ и «ВВЕСТИ В ЖИЗНЬ, где она проявляет величайшее, свойственное пустому высокомерию СЕБЯЛЮБИЕ, она чаще всего говорит о НАРОДЕ.

Но особо ее отличает НЕНАВИСТЬ К ЗАКОНУ. В том, что право и нравственность и подлинный мир права и нравственного постигают себя посредством МЫСЛИ, посредством мысли сообщают себе форму РАЗУМНОСТИ, а именно ВСЕОБЩНОСТЬ и ОПРЕДЕЛЕННОСТЬ, в этом, в ЗАКОНЕ, это чувство, оставляющее за собой право на произвол, эта совесть, перемещающее правое в область субъективного убеждения, с полным основанием видит наиболее враждебное для себя. ФОРМА ПРАВОГО как ОБЯЗАННОСТИ и ЗАКОНА воспринимается этим чувством как МЕРТВАЯ, ХОЛОДНАЯ БУКВА, как ОКОВЫ, ибо оно не познает в нем самого себя, не познает себя в нем свободным, поскольку закон есть разум предмета, и этот разум не дозволяет чувству согреваться своей собственной частной обособленностью. Поэтому ЗАКОН, как мы отметили где-то в данной работе, — тот признак, по которому можно отличить ложных братьев и друзей так называемого народа». (Гегель. Философия права. М.: Мысль, 1990. С. 50.)

В истории математики тоже существовало такое время, когда со словом ЗАКОН ассоциировался не инвариантный объект, тождественный сам себе, а лишь ПРАВИЛО, по которому одному математическому объекту ставился во «взаимно однозначное соответствие» — другой математический объект. В настоящее время вся совокупность таких правил рассматривается (говоря языком геометрии), как ПРАВИЛА преобразования координат, а то, что остается при преобразованиях координат БЕЗ ИЗМЕНЕНИЯ и есть ИНВАРИАНТ.

Координатные представления теперь отождествляют с той или иной субъективной точкой зрения (в физике — это различие «наблюдателей»), а ИНВАРИАНТ — это то, что не зависит от частной точки зрения. Но именно ЗАКОНЫ ПРИРОДЫ и есть то, что не зависит от точки зрения того или иного человека, причисляющего себя или не причисляющего себя к сообществу мировой науки.

Итак, если бы человечество не создало мира математики, то оно никогда не смогло бы обладать НАУКОЙ. Только мир математики и позволил человечеству получить понятие «ЗАКОН», как то, над чем не властно даже ВРЕМЯ. Это и есть ответ на наш первый вопрос: почему человечество (с необходимостью, присущей случаю) должно было придумать математику? Не следует думать, что описанное выше принадлежит авторам: известно библейское выражение — «и это было...» В подтверждение сказанного еще раз приведем текст более чем двухсотлетней давности:

«учение о природе будет содержать науку в собственном смысле лишь в той мере, в какой может быть применена в нем математика...» (И.Кант. Соч. Т. 6. М.: Мысль, 1966. С. 55—57.)

3. Почему математика устроена аксиоматически?

Для начала приведем несколько «аксиом», которые вне геометрии принято называть «исходными правильными формулами».

Рассмотрим три выражения: 1 + 1 = 2; 1 + 1 = 1; 1 + 1 = 0.

Все три приведенные выше формулы представляют собой иллюстрацию алгоритмически неразрешенных проблем. Можно ли доказать «истинность» этих «исходных правильных формул»? Философская наивность Д.Гильберта в попытках доказать «непротиворечивость арифметики» — естественное следствие членения наук по «факультетам». Не менее наивно представление о выпускнике философского факультета университета, что дипломант имеет не руках удостоверение «философа». Как математика, так и философия развиваются человечеством уже много более двух тысячелетий и имеются трудности в освоении этих двух областей.

Все три приведенные формулы мы можем привести к общему виду. Для этого заменим одинаковые выражения в левых частях буквой А. Поскольку все правые части отличаются по написанию от левой, а также друг от друга, то заменим их буквами B, C, D соответственно:

A = B; A = C; A = D.

Следуя за Гильбертом (но не за Брауэром и Вейлем), попробуем использовать принцип «исключенного третьего».

Относительно любой буквы справа мы можем задавать вопрос: «Есть ли она буква А “или” не- А?» Совершенно очевидно, что мы три раза получим ответ: «не- А»!

Запишем этот результат. Все формулы приобретают один и тот же вид:

А = не- А; А = не- А; А = не- А.

Нетрудно видеть, что ЛЮБАЯ ИСХОДНАЯ ПРАВИЛЬНАЯ ФОРМУЛА, у которой правая часть от знака равенства только ПО НАПИСАНИЮ отличается от левой части от знака равенства, в соответствии с «законом исключенного третьего» будет приведена к ПРОТИВОРЕЧИЮ. Этот факт был всегда известен серьезным математикам, что привело к предложению О.Веблена и Дж.Юнга в их «Проективной геометрии» начала нашего века заменить математический термин «аксиома» на более подходящий термин «ПРЕДПОЛОЖЕНИЕ».

Однако, как известно тоже около двухсот лет в философии, каждому ПОЛОЖЕНИЮ соответствует некоторое ПРОТИВОПОЛОЖЕНИЕ (по-немецки первому соответствует термин «Satz», а второму «Gegensatz»), что предполагает НЕОБХОДИМОСТЬ рассматривать КАЖДОЕ положение вместе с его противоположением. Если классические аксиомы геометрии, как систему предположений, отождествить с именами творцов математики, то мы получим СДВОЕННЫЕ геометрии: Евклидова и не-евклидова, Архимедова и не-архимедова, Дезаргова и не-дезаргова, Паскалева и не-паскалева, и т.д.

В философии за термином «КАТЕГОРИАЛЬНАЯ ПАРА» стоит утверждение, в котором встречаются ДВА ПРОТИВОПОЛОЖНЫХ ПРЕДИКАТА. Именно противоположные предикаты и носят название «категориальных пар». Первый шаг к рассмотрению «категориальных пар» в математике был совершен Н.И.Лобачевским и Я.Бойяи. Но это и был тот шаг, который демонстрирует ПЕРЕХОД от традиционной математической логики к логике диалектической. Про последнюю наговорено столько нелепостей, что о ее значении для МАТЕМАТИКИ почти ничего не известно. Диалектическая логика — это логика, которая относится ТОЛЬКО к аксиомам или ПРЕДПОЛОЖЕНИЯМ математических теорий. Лучше всего об этом в своем философском конспекте писал Н.И.Лобачевский:

«Общая логика называется также АНАЛИТИКОЮ, равно как и прикладная логика — ДИАЛЕКТИКОЮ». (Н.И.Лобачевский. Научно-педагогическое наследие... М.: Наука, 1976. С. 581.)

В этом же конспекте он демонстрирует полное понимание различия мира математических объектов от объектов окружающего мира: он понимает, что математические следствия из математических предположений всегда были, есть и будут «истинными в математическом смысле». Но наличие ВОЗМОЖНОГО противоречия выводов из математической теории с реальностью только указывает, что мы используем теорию за границами нами же установленных ПРЕДПОЛОЖЕНИЙ. Аналогичную позицию по отношению к математическим теориям занимал и Дж.К.Максвелл. Только удержание в поле зрения как положений, так и противоположений, ОБЕРЕГАЕТ наше математическое мышление от догматизма. Здесь же и расположена область математического творчества: либо мы рассматриваем в известной области некоторое противоположение, на которое ранее не обращалось внимания, либо мы порождаем новую аксиоматическую пару, создавая новое математическое направление.

Учитывая, что в основаниях геометрии Д.Гильберта представлено всего 16 аксиом, то, рассматривая их парами, мы можем получить 216 геометрий! Но мы до сих пор не научились «узнавать их в лицо». Здесь и случилось то, что «освоив» аксиоматический метод, некоторые «математики», как правильно заметили Н.Бурбаки в своей «Архитектуре математики», кинулись «творить». Они пишут:

«Мы были свидетелями также, особенно в то время, когда аксиоматический метод только что начал развиваться, расцвета уродливых структур, ПОЛНОСТЬЮ ЛИШЕННЫХ ПРИЛОЖЕНИЙ». (Н.Бурбаки. Очерки по истории математики. М.: ИИЛ, 1962. С. 257.)

Основной вывод из этого раздела состоит в том, что любое высказывание, утверждение или ПОЛОЖЕНИЕ, высказанное на естественном языке, не является той ЛОГИЧЕСКОЙ ФОРМОЙ, в которой выражается ИСТИНА. Не существует НИ ОДНОГО ВЫСКАЗЫВАНИЯ («ПОЛОЖЕНИЯ»), которое может быть ФОРМОЙ выражения ИСТИНЫ. Значительно труднее освоить ОТРИЦАНИЕ этого положения, выраженное в диалектической форме. Всякая исходная логическая форма, содержащая ПРОТИВОРЕЧИЕ, является той формой, в которой фиксируется «исходная правильная формула». Мы это демонстрировали в виде трех формул в начале этого раздела:

1 + 1 = 2; 1 + 1 = 1; 1 + 1 = 0.

Математический СМЫСЛ этих трех утверждений весьма прост. Первая формула принадлежит арифметике. Вторая — это формула алгебры Буля, утверждающая, что «универсальное множество (обозначенное как “1”) будучи сложено с самим собой — есть то же самое универсальное множество». Третья формула определяет сложение по модулю 2. Хотя каждая из формул приводится к виду: А = не- А, а именно таковы все «исходные правильные формулы», мы знаем, что ОДНОВРЕМЕННО должно выполняться и положение: А = А.

Наличие работ с высказыванием, или положением, которое имеет вид математической аксиомы, сопровождает процесс ОСМЫСЛИВАНИЯ: «А есть В» и «В есть А» — отождествление. Оно означает РАВЕНСТВО А и В в некотором «отношении». Но одновременно с этим существует еще и НЕРАВЕНСТВО А и В: «А не-есть В» и «В не-есть А» — противопоставление.

Стандартное представление этих двух ПРОТИВОположений принято в тензорном анализе, где ИНВАРИАНТ — есть то, что ОДНО И ТО ЖЕ. Его же матричное представление может менять свой вид, но лишь ЗНАНИЕ, что это матричные представления одного и того же инвариантного объекта, РАЗРЕШАЕТ алгоритмически неразрешимую проблему.

«Визуализацию» этого положения очень хорошо демонстрировал П.С.Новиков. Он показывает точку, поставленную карандашом на бумаге. Затем предлагает представить себе координатную сетку, нарисованную на кальке. Накладывая эту координатную сетку на бумагу с изображением точки, мы получаем запись А ( 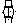, 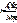), где 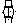, 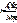— координаты нашей точки в первой координатной системе. Затем берем вторую координатную сетку на кальке и кладем ее сверху первой сетки. Во второй координатной системе та же самая точка получает координаты B ( , ), где , — координаты нашей точки во второй системе координат. Теперь мы можем получить выражение, которое соответствует булевой переменной:

«Являются ли координаты A ( 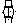, 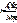) координатами ТОЙ ЖЕ САМОЙ ТОЧКИ, которая имеет координаты B ( , ) во второй системе координат?»

Вот здесь возможен ОДИН И ТОЛЬКО ОДИН ОТВЕТ: либо «ДА», либо «НЕТ».

Никакой другой способ не дает «математически чистого» определения булевой переменной. Теперь мы можем получить и ПОНЯТИЕ «АЛГОРИТМ».

Это ПРАВИЛО- F, которое позволяет по координатам ОДНОЙ И ТОЙ ЖЕ ТОЧКИ, данным в первой системе координат, найти координаты той же самой точки во второй системе координат.

B ( , ) = F & A ( , ).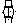

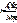Фактически существуют три правила, которые позволяют математику говорить «СЛЕДОВАТЕЛЬНО»:

1. 1. Если А > B и B > C, то, следовательно, A > C.

2. 2. Если A = B и B = C, то, следовательно, A = C.

3. 3. Если A Î B и B Î C, то, следовательно, A Î C.

Устройство математики, благодаря ее аксиоматической конструкции, позволяет передавать ВСЕ, ЧТО ПОНЯТО в вычислительную машину. Это открывает возможность создания «банка теорий», охватывающих все предметные области, т.е. все профессиональные знания.

Подведем итог: аксиомы, которые правильно называть ПРЕДПОЛОЖЕНИЯМИ, не могут рассматриваться без своего «отрицания», т.е. ПРОТИВОПОЛОЖЕНИЯ. Всякое ПОЛОЖЕНИЕ во всех случаях имеет ГРАНИЦУ, за пределами которой оно «превращается» в свою ПРОТИВОПОЛОЖНОСТЬ. Этот переход за ненаблюдаемую в математике ГРАНИЦУ, есть изменение КАЧЕСТВА. Этот переход через ГРАНИЦУ, т.е. переход к другому КАЧЕСТВУ, порождает известные математические «трудности»: нелинейность, бифуркацию, катастрофу и т.п. — математические термины, выражающие РАЗРЫВ непрерывности, СКАЧЕК или изменение ПРАВИЛА.

Именно И.Кант обнаружил, что невозможно описывать реальный мир, если пользоваться ТОЛЬКО УТВЕРДИТЕЛЬНЫМИ ВЫСКАЗЫВАНИЯМИ. Оказалось, что мы нуждаемся в ОТРИЦАТЕЛЬНЫХ высказываниях. Отдельные части реальности удовлетворяют утвердительным положениям, но существуют и такие части реальности, которые требуют ОТРИЦАНИЯ этих утвердительных положений. Анализ этой ситуации и привел к признанию сосуществования как утверждения, так и его отрицания. Объединение того и другого философы называют СИНТЕЗИСОМ, который охватывает как ТЕЗИС, так и АНТИТЕЗИС. Новое КАЧЕСТВО — есть НОВЫЙ ОБЪЕКТ. Именно он и есть ИНВАРИАНТ математического описания, а «старые» тезис и антитезис — есть не более как его «координатные представления».

4. О единстве и целостности математики

Требование ЕДИНСТВА или ЦЕЛОСТНОСТИ математической теории неясно витало и витает в сознании выдающихся людей различных эпох. Уже в своеобразном «манифесте» группы Н.Бурбаки мы встречаем крушение замысла унификации всей математики у пифагорейцев — «все вещи суть числа», но открытие иррациональности — отвергло эту попытку унификации. Хотя и принято считать, что унификации математики посвящено многотомное издание Н.Бурбаки, мы хотели бы выделить Эрлангенскую программу Ф.Клейна в качестве первой современной попытки унификации ВСЕЙ МАТЕМАТИКИ (1872 г.).

5. Математика и геометрия

Догадка, которой руководствовался Ф.Клейн, состояла в том, что ВСЯ математика может быть представлена как разновидности ПРОЕКТИВНОЙ ГЕОМЕТРИИ. Он писал:

«Между приобретениями, сделанными в области геометрии за последние пятьдесят лет, развитие проективной геометрии занимает первое место. Если в начале казалось, что для нее недоступно изучение так называемых метрических свойств, так как они не остаются без изменения при проектировании, то в новейшее время научились представлять и их с проективной точки зрения, так что теперь проективный метод охватывает всю геометрию». (Об основаниях геометрии. М., ГИТТЛ, 1956. С. 399.) Ф.Клейн считал, что ему удалось специфицировать типы геометрий с помощью ГРУПП ПРЕОБРАЗОВАНИЙ КООРДИНАТ.

Не очень бросается в глаза, что метрика, доступная проективной геометрии — это метрика, которая позволяет разделить на две равные части отрезок или увеличить отрезок в два раза. Таким образом эта метрическая шкала состоит из чисел, которые кратны 2 n или 2 - n. Само собою разумеется, что это дискретная шкала, которая (в прикладных теориях, использующих вычислительные машины) вполне достаточна для всех технических приложений.

Другой подход к единству ВСЕЙ ГЕОМЕТРИИ был продемонстрирован Д.Гильбертом в его работах по основаниям геометрии. Гильберт положил в основу различия геометрий — различие в использовании АКСИОМ. Рассматривая каждую аксиому и ее отрицание, Гильберт предъявил не только не-евклидовы геометрии, но и не-дезарговы, не-архимедовы, не-паскалевы и др. геометрии. У Гильберта было введено 16 аксиом. Если считать, что все приведенные им аксиомы НЕЗАВИСИМЫ, то мы должны обозревать и «узнавать в лицо» — 216 геометрий, каждая из которых может быть выделена последовательностью из нулей и единиц (в зависимости от принятия данной аксиомы — 1, а если данная аксиома отрицается, то 0) — 65 536 различных геометрий. При интерпретации каждой в той или иной предметной области — мы можем получить такое количество качественно различных физических теорий.

Третий подход к единству ВСЕЙ ГЕОМЕТРИИ идет от О.Веблена. Не задерживаясь на антагонизме геометрий Клейна и Римана, блестяще разобранных Э.Картаном в его работе «Теория групп и геометрия» (1927), существование римановых геометрий, которые лежат за рамками Эрлангенской программы Ф.Клейна, привело О.Веблена и Дж.Уайтхеда к работе «Основания дифференциальной геометрии». Там О.Веблен упоминает о своем докладе на международном математическом конгрессе в Болонье. О.Веблен ожидал синтеза всех геометрий, как «...теорию пространств с инвариантом». Здесь мы встречаемся с понятием «РАЗМЕРНОСТЬ», которое будет иметь весьма важное значение в нашем последующем изложении. Развитием этого направления служит четырехтомное издание работ японской ассоциации прикладной геометрии (RAAG), изданных в 1955—1968 гг. на основе работ Г.Крона.

Хотя японская ассоциация и объявила работы Г.Крона «Новой эпохой в науке», только в Японии мы находим развитие идей Г.Крона. К сожалению в России и Европе идеи Г.Крона малоизвестны.

Многие ли математики в то время были знакомы с возможными обобщениями N -мерных пространств, о которых пишет Г.Крон (1939 г.):

«... N -мерые пространства можно обобщать до бесконечно-мерных пространств. Кроме того, вместо использования только четырех-, пяти- и вообще целочисленно-размерных пространств можно использовать 2/3-, 4,375- или p -мерные пространства, включающие все типы сложных структур. Эти пространства используются в исследовании более фундаментальных электродинамических явлений».

Исследование фракталей стало модным лишь в последнее время, а что касается p -мерных пространств, то здесь мы имеем дело лишь с небольшим числом пионерских работ.

Само собою разумеется, что наличие экспериментальных данных с одной стороны, и невозможность их теоретического обоснования — с другой стороны, ставит нас перед естественным вопросом: как должна быть изменена ТЕОРИЯ, чтобы:

1) она СОХРАНЯЛА действующую ТЕОРИЮ там, где ее выводы соответствуют (и нашли экспериментальное подтверждение) наблюдаемым фактам;

2) она ИЗМЕНЯЛА действующую ТЕОРИЮ там, где ее выводы не соответствуют некоторой группе экспериментальных данных (лежащих за ГРАНИЦЕЙ существующей ТЕОРИИ).

Не подлежит никакому сомнению, что подобное РАСШИРЕНИЕ действующей теории должно включать в себя (но уже на правах ЧАСТНОГО СЛУЧАЯ) уже СУЩЕСТВУЮЩУЮ теорию (теории).

Ответ лежит не в области физики, а в области математики. Мы должны РАЗЛИЧАТЬ те положения, которые принадлежат миру МАТЕМАТИКИ, от тех положений, которые связаны с ФИЗИЧЕСКОЙ ИНТЕРПРЕТАЦИЕЙ математической теории.

6. Устройство математических теорий

Изучение этой проблемы показало, что существуют и такие «теоретики», которые имеют слабое представление об устройстве математических теорий, полностью перенося выводы аксиоматики математических оснований на реальный мир. Для математической теории нет и не может быть ГРАНИЦ применимости: в математической теории ВСЕГДА получаемые выводы находятся в соответствии с принятыми ПРЕД-посылками. Это соответствие СЛЕДСТВИЙ принятым ПРЕД-посылкам называется ИСТИННОСТЬЮ математической теории. В этом смысле математик может заменять некоторые предпосылки на то, что раньше называлось следствием, но при этом сама математическая теория не теряет своей истинности. Такую переработку некоторых математических теорий совершила группа, публиковавшая свои материалы под псевдонимом Н.Бурбаки. Многотомное издание современной математики группой Н.Бурбаки имело своим основанием своеобразный «стандарт» или «технические условия», которым должна удовлетворять любая МАТЕМАТИЧЕСКАЯ теория. Этот же «стандарт» применяется и при переходе от одной теории к другой.

Заметим, что «стандарт», определенный для устройства математических теорий, данный Бурбаки, является НЕОБХОДИМЫМ для передачи формальной теории в вычислительную машину.

Рассмотрим «стандарт», который предложен группой Н.Бурбаки.

Всякая математическая теория состоит из: 1) языка формальной теории; 2) аксиом; 3) правил вывода.

Наличие указанных трех составных частей характеризует ЛЮБУЮ МАТЕМАТИЧЕСКУЮ ТЕОРИЮ. Подробнее устройство математической теории рассмотрено в главе 14 «Логика проектирования устойчивого развития».

7. Отличие математического языка от естественного

Введенный группой Н.Бурбаки язык — язык теории множеств — являясь унифицированным языком математики, имеет кардинальное отличие от естественного языка. В математической теории не только следствия находятся в однозначном соответствии с принятыми предпосылками, но имеется такое же взаимнооднозначное соответствие между ТЕРМОМ (или термином) и обозначаемым этим термом математическим ОБЪЕКТОМ.

Математический объект всегда выведен из под действия ВРЕМЕНИ. Это выражается в том, что некоторые формулы принято называть в математике АТОМАМИ (или АТОМАРНЫМИ ВЫСКАЗЫВАНИЯМИ). Атом несет в себе два значения: неделимый и объект, который не изменяется с ходом действительного времени. Последнее должно означать, что обозначенный этим термом или соотношением объект так же не изменяется, как не изменяется (по написанию) его «имя».

Дата добавления: 2014-11-29