
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Пример К2
|
|
|
|
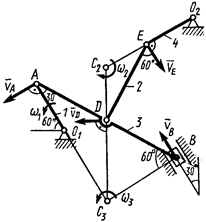
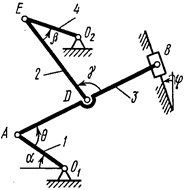 Механизм (рис. К2,а) состоит из стержней 1, 2, 3, 4 и ползуна
Механизм (рис. К2,а) состоит из стержней 1, 2, 3, 4 и ползуна  , соединенных друг с другом и с неподвижными опорами
, соединенных друг с другом и с неподвижными опорами  и
и  шарнирами.
шарнирами.
 Дано:
Дано: 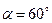 ,
, 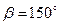 ,
, 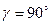 ,
, 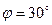 ,
,  ,
, 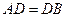 ,
, 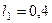 м,
м, 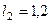 м,
м, 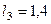 м,
м,  с-1,
с-1, 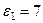 с-2 (направления
с-2 (направления 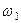 и
и 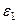 – против хода часовой стрелки).
– против хода часовой стрелки).
Определить: 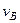 ,
, 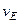 ,
, 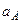 ,
, 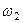 .
.
Решение:
1. Строим положение механизма в соответствии с заданными углами и выбранным масштабом длин (рис. К2,б; на этом рисунке изображаем все векторы скоростей).
 2. Определяем
2. Определяем  . Точка
. Точка  принадлежит стержню
принадлежит стержню  . Чтобы найти
. Чтобы найти 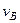 , надо знать скорость какой-нибудь другой точки этого стержня и направление
, надо знать скорость какой-нибудь другой точки этого стержня и направление 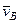 . По данным задачи, учитывая направление
. По данным задачи, учитывая направление 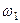 , можем определить
, можем определить 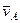 . Численно:
. Численно:
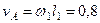 м/с,
м/с,
 . (1)
. (1)
 Направление
Направление 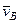 найдем, учтя, что точка
найдем, учтя, что точка  принадлежит одновременно ползуну, движущемуся вдоль направляющих поступательно. Теперь, зная
принадлежит одновременно ползуну, движущемуся вдоль направляющих поступательно. Теперь, зная 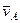 и направление
и направление 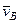 , воспользуемся теоремой о проекциях скоростей двух точек тела (стержня
, воспользуемся теоремой о проекциях скоростей двух точек тела (стержня 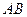 ) на прямую, соединяющую эти точки (прямая
) на прямую, соединяющую эти точки (прямая 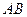 ). Сначала по этой теореме устанавливаем, в какую сторону направлен вектор
). Сначала по этой теореме устанавливаем, в какую сторону направлен вектор 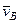 (проекции скоростей должны иметь одинаковые знаки). Затем, вычисляя эти проекции, находим
(проекции скоростей должны иметь одинаковые знаки). Затем, вычисляя эти проекции, находим
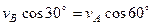 ,
, 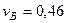 м/с. (2)
м/с. (2)
3. Определяем 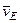 . Точка
. Точка 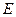 принадлежит стержню
принадлежит стержню 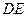 . Следовательно, по аналогии с предыдущим, чтобы определить
. Следовательно, по аналогии с предыдущим, чтобы определить 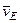 , надо сначала найти скорость точки
, надо сначала найти скорость точки 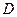 , принадлежащей одновременно стержню
, принадлежащей одновременно стержню 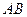 . Для этого, зная
. Для этого, зная 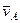 и
и 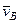 , строим мгновенный центр скоростей (МЦС) стержня
, строим мгновенный центр скоростей (МЦС) стержня 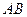 . Это точка
. Это точка 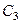 , лежащая на пересечении перпендикуляров к
, лежащая на пересечении перпендикуляров к 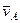 и
и 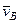 , восставленных из точек
, восставленных из точек 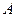 и
и 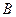 (к
(к 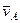 перпендикулярен стержень 1). По направлению вектора
перпендикулярен стержень 1). По направлению вектора 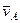 определяем направление поворота стержня
определяем направление поворота стержня 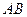 вокруг МЦС
вокруг МЦС 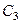 . Вектор
. Вектор 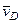 перпендикулярен отрезку
перпендикулярен отрезку 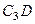 , соединяющему точки
, соединяющему точки 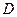 и
и 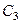 , и направлен в сторону поворота. Величину
, и направлен в сторону поворота. Величину 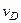 найдем из пропорции:
найдем из пропорции:
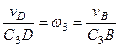 . (3)
. (3)
Чтобы вычислить 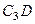 и
и  , заметим, что
, заметим, что 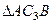 – прямоугольный, так как острые углы в нем равны 30° и 60°, и что
– прямоугольный, так как острые углы в нем равны 30° и 60°, и что 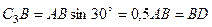 . Тогда
. Тогда 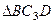 является равносторонним и
является равносторонним и 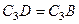 . В результате равенство (3) дает
. В результате равенство (3) дает
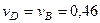 м/с,
м/с,  . (4)
. (4)
Так как точка 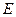 принадлежит одновременно стержню
принадлежит одновременно стержню  , вращающемуся вокруг
, вращающемуся вокруг 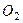 , то
, то 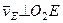 . Тогда, восставляя из точек
. Тогда, восставляя из точек 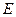 и
и 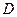 перпендикуляры к скоростям
перпендикуляры к скоростям 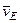 и
и 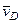 , построим МЦС
, построим МЦС 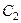 стержня
стержня 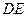 . По направлению вектора
. По направлению вектора 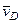 определяем направление поворота стержня
определяем направление поворота стержня 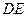 вокруг центра
вокруг центра 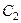 . Вектор
. Вектор 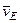 направлен в сторону поворота этого стержня. Из рис. К2,б видно, что
направлен в сторону поворота этого стержня. Из рис. К2,б видно, что 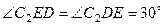 , откуда
, откуда 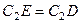 . Составив теперь пропорцию, найдем, что
. Составив теперь пропорцию, найдем, что
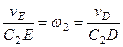 ,
, 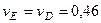 м/с. (5)
м/с. (5)
4. Определяем 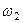 . Так как МЦС стержня 2 известен (точка
. Так как МЦС стержня 2 известен (точка 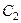 ) и
) и 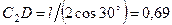 м, то
м, то
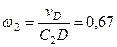 с–1. (6)
с–1. (6)
5. Определяем 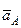 (рис. К2,в, на котором изображаем все
(рис. К2,в, на котором изображаем все  векторы ускорений). Точка
векторы ускорений). Точка 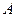 принадлежит стержню 1. Полное ускорение точки
принадлежит стержню 1. Полное ускорение точки 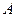 разложим на тангенциальную и нормальную составляющие:
разложим на тангенциальную и нормальную составляющие:
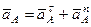 ,
,
где численно
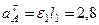 м/с2,
м/с2,
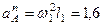 м/с2. (7)
м/с2. (7)
 Вектор
Вектор 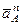 направлен вдоль
направлен вдоль 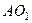 , а
, а  – перпендикулярно
– перпендикулярно 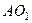 . Изображаем эти векторы на чертеже (см. рис. К2в). Вычисляем
. Изображаем эти векторы на чертеже (см. рис. К2в). Вычисляем
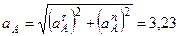 м/с2.
м/с2.
Ответ: 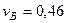 м/с,
м/с, 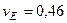 м/с,
м/с, 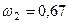 с–1,
с–1, 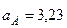 м/с2.
м/с2.
КОНТРОЛЬНЫЕ ВОПРОСЫ
Задача С1
1) Основные виды силовых воздействий и их свойства:
– сосредоточенная сила (проекции силы на оси; момент силы относительно точки как характеристика вращательного действия силы; величина и знак алгебраического момента;
– вращающий момент (пара сил), изображение пары на плоскости, момент пары;
– распределенные силы с постоянной интенсивностью (эпюра распределенных сил, приведение к равнодействующей).
2) Силы активные и реакции связей. Внешние закрепления конструкции (подвижный и неподвижный цилиндрические шарниры, скользящая заделка – втулка, жесткая заделка, невесомый стержень, нить, идеальная поверхность). Как направлены реакции этих связей? Сколько неизвестных составляющих реакции имеет каждая из перечисленных связей? В каком случае реакция связи содержит вращающий момент?
3) Виды представленных в конструкциях соединений тел между собой. Метод разбиения. Внутренние двусторонние и односторонние связи.
4) Каковы аналитические условия равновесия произвольной плоской системы сил?
5) Статическая определимость и неопределимость конструкции. Какие дополнительные условия представлены в задаче, которые делают конструкцию статически определимой? Как определяется статическая определимость в сочлененных конструкциях?
Задача К1
1) Координатный способ задания движения точки.
2) Определение скорости точки. Нахождение скорости при координатном способе задания движения.
3) Определение ускорения. Разложение ускорения на касательную и нормальную составляющие.
4) Естественный способ изучения движения. Определение кинематических характеристик в естественных координатах.
Задача К2
1) Виды движений различных звеньев плоского механизма задачи К2.
2) Поступательное движение.
3) Вращательное движение вокруг неподвижной оси (центра 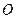 ). Угловая скорость и угловое ускорение вращающихся звеньев. Как направлены и чему равны скорости точек вращающегося тела?
). Угловая скорость и угловое ускорение вращающихся звеньев. Как направлены и чему равны скорости точек вращающегося тела?
4) Плоскопараллельное движение. Мгновенный центр скоростей и его свойства. Как найдены МЦС звеньев механизма задачи?
5) Как формулируется теорема о проекциях скоростей двух точек тела? Как она используется для нахождения скоростей различных точек механизма?
|
|
|
|
|
Дата добавления: 2014-12-16; Просмотров: 532; Нарушение авторских прав?; Мы поможем в написании вашей работы!