Метод итерации

Пример

На Рисунке 9 показано решение системы линейных уравнений методом Гаусса, в котором используются следующие функции:

rref(A)

Возвращается ступенчатая форма матрицы А.

augment(A, В)

Возвращается массив, сформированный расположением A и В бок о бок. Массивы A и В должны иметь одинаковое число строк.

submatrix(A, ir, jr, ic, jc)

Возвращается субматрица, состоящая из всех элементов с ir по jr и столбцах с ic по jc. Удостоверьтесь, что ir 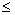jr и

ic 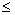jc, иначе порядок строк и (или) столбцов будет обращен.

Пусть дана линейная система (13). Введя в рассмотрение матрицы (15), систему (13) коротко можно записать в виде матричного уравнения (14). Предполагая, что диагональные коэффициенты a_ij не равны 0 (i = 1, 2, …, n),

разрешим первое уравнение системы (13) относительно х ₁, второе - относительно х ₂ и т. д. Тогда получим эквивалентную систему

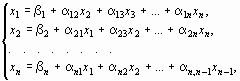
(18)

где

при i не равно j

и  _ij = 0 при i = j (i, j = 1, 2, …, n).

Введя матрицы

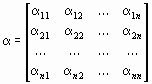и ,

систему (18) можно записать в матричной форме

x =  +  x,

а любое (k + 1) приближение вычисляется по формуле

x ^(k+1) =  +  x ^(k).

(19)

Напишем формулы приближений в развернутом виде:

(19')

Приведем достаточное условие сходимости метода итераций.

Теорема: Процесс итерации для приведенной линейной системы (18) сходится к единственному ее решению, если какая-нибудь каноническая норма матрицы  меньше единицы, т.е. для итерационного процесса (19) достаточное условие есть

(20)

Следствие 1. Процесс итерации для системы (18) сходится, если:

1) < 1 (m- норма или неопределенная норма)

или

2) < 1 (l- норма или норма L 1)

или

3) < 1 (k- норма или Евклидова норма).

Следствие 2. Для системы (13) процесс итерации сходится, если выполнены неравенства:

или ,

где штрих у знака суммы означает, что при суммировании пропускаются значения i = j, т. е. сходимость имеет место, если модули диагональных элементов матрицы А системы (13) или для каждой строки превышают сумму модулей недиагональных элементов этой строки, или же для каждого столбца превышают сумму модулей недиагональных элементов этого столбца.

Пример 6. Пусть

.

Имеем:

max(1+ 2 + 3, 4 + 5 + 6, 7 + 8 + 9) = max (6, 15, 24) = 24;

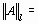max(1+ 4 + 7, 2 + 5 + 8, 3 + 6 + 9) = max (12, 15, 18) = 18;

.

В Mathcad существуют специальные функции для вычисления норм матриц:

normi(A)

Возвращает неопределенную норму матрицы А.

norm1(A)

Возвращает L 1, норму матрицы А.

normе(A)

Возвращает Евклидову норму матрицы А.

В качестве условия окончания итерационного процесса можно взять условие

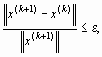
 - заданная погрешность приближенного решения х  x ^{(k + 1)}.

Пример7. Решить систему

(21)

методом итераций.

Диагональные коэффициенты 100; 200; 100 системы (21) значительно преобладают над остальными коэффициентами при неизвестных, т.е., выполняется следствие 2.

Приведем эту систему к нормальному виду (18)

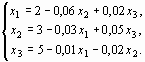
В матричной форме ее можно записать так:

.

Рисунок 10.

На Рисунке 10 приведен фрагмент рабочего документа Mathcad, содержащий дальнейшее решение этой системы.

Дата добавления: 2014-12-16