Введение

Х 897

12 13 14 15

1 2 3 4 5 6 7 8 9 10 11

12 13 14 15 16 17 18 19

1 2 3 4 5 6 7 8 9 10 11

1 2 3 4 5 6 7,

Ответы.

Задача 1.

1) Ответы на первый вопрос дадим в форме deg(v)=deg ^- (v)+deg⁺(v):

deg(v₁) = 1+2=3; deg(v₂) = 2+1=3; deg(v₃) = 1+2=3;

deg(v₄) = 2+1=3; deg(v₅) = 1+1=2; deg(v₆) = 1+1=2.

2) Не имеет.

3) Имеет, например, простой цикл v₁, v₃, v₅ длины 3.

4) Орграф является связным, т.к. для двух произвольных вершин

существует путь, идущий из одной из вершин в другую.

5) Граф, ассоциированный с исходным орграфом, имеет вид:

v₁v₂

v₃v₄

v₅v₆

6) Простой путь наибольшей длины v₃, v₅, v₁, v₂, v₆, v₄ длины 5.

7) Девять путей длины 2: v₁, v₃, v₅; v₁, v₂, v₆; v₂, v₆, v₄; v₃, v₅, v₁; v₃, v₄, v₂;

v₄, v₂, v₆; v₅, v₁, v₃; v₅, v₁, v₂; v₆, v₄, v₂.

8) Если занумеровать ребра графов следующим образом

(v₁, v₃), ( v₁, v₂), ( v₄, v₂), (v₅, v₁), (v₆, v₂), (v₃, v₅), (v₆, v₄)

то матрицы инцидентности графа G и ассоциированного с ним графа G’ следующие:

,

.

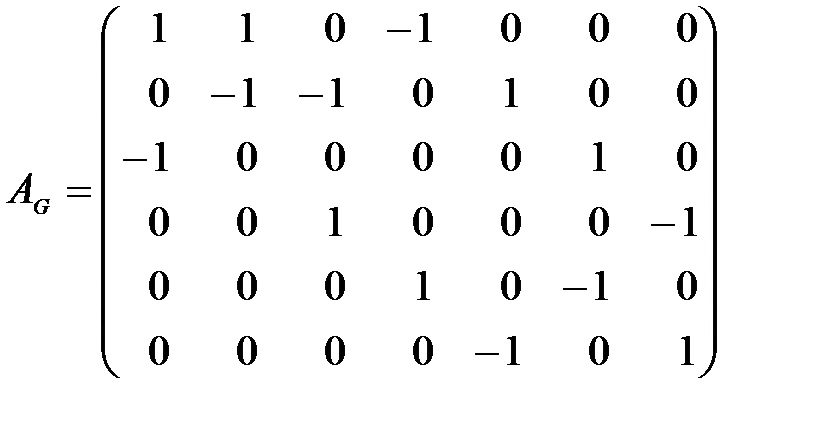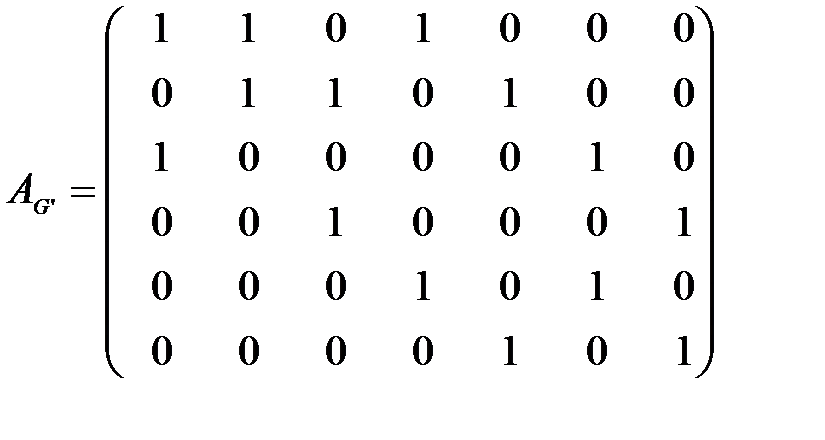9) Матрицы смежности графа G и ассоциированного с ним графа G’ следующие:

, .

10) И исходный граф G, и ассоциированный с ним граф G’ являются плоскими, поскольку, например, следующее их геометрическое задание удовлетворяет требованиям правильной укладки графов в пространство E²:

v₁v₂

v₃v₄

v₅v₆

Задача 2. Геометрическое задание графов на основании матрицы инцидентности выполняется непосредственно по определению матрицы, а потому выполнить этот шаг, а также ответы на вопросы 1) – 9), самостоятельно (с учетом задачи 7.1).

Непосредственно по матрице инцидентности орграфа можно получить следующую информацию:

1) Найти полустепени захода и исхода для каждой вершины. Для этого достаточно зафиксировать соответствующую строку и подсчитать количество (-1) – получим полустепень захода вершины или количество 1 – получим полустепень исхода. Сумма полустепеней захода и исхода определит степень соответствующей вершины. В нашем случае (deg(v)=deg ^- (v)+deg⁺(v)) имеем:

deg(v₁)=2+2 =4; deg(v₂)=1+1=2; deg(v₃)=2+1=3;

deg(v₄)=2+1=3; deg(v₅)=1+3=4.

2) Определить тип графа (псевдограф, мультиграф, обыкновенный граф). В нашем случае граф не имеет петель (в строке была бы единица помеченная сразу и плюсом и минусом) и не имеет кратных ребер (иначе в графе были бы одинаковые столбцы). Следовательно орграф – обыкновенный.

3) Орграф не имеет стоков (в матрице была бы строка, содержащая только +1) и не имеет источников (в строке матрицы содержались бы только -1).

4) Орграф не имеет изолированных вершин (иначе в матрице существовала бы нулевая строка).

5) На основании матрицы инцидентности для каждой вершины можно найти ее множества предшественников O^-1(v) и преемников O⁺(v) (а, значит, и окружение O(v)), но это осуществляется не так наглядно, как поиск предыдущих характеристик. Например, для того, чтобы найти множество предшественников вершины v₃ необходимо зафиксировать третью строку матрицы и определить все ребра, для которых эта вершина является концом (зафиксировать -1 в строке и столбцы, которые содержат эти -1). Затем в этих столбцах найти 1 и по номерам строк, содержащих эти 1, зафиксировать вершины орграфа. Их множество и задает множество предшественников исходной вершины. В нашем случае O^-1(v₃) = {v₁, v₂}. Аналогично находится множество преемников вершины. Например, O⁺(v) = {v₅}. Таким образом, O(v) = {v₁, v₂, v₅}.

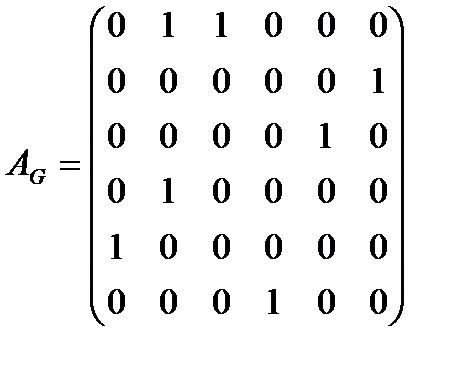
Матрица смежности для графа, ассоциированного с исходным орграфом, следующая

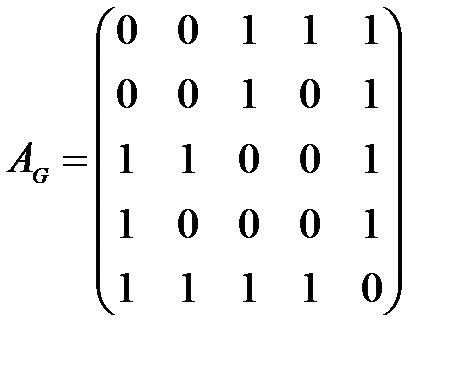
Задача 3. Геометрическое задание графов на основании матрицы смежности выполняется непосредственно по определению матрицы, а потому выполнить этот шаг, а также ответы на вопросы 1) – 9), самостоятельно (с учетом задачи 7.1).

Непосредственно по матрице смежности графа можно получить следующую информацию:

1) Поскольку матрица смежности не является симметрической относительно главной диагонали, то граф с такой матрицей смежности является орграфом.

2) Этот орграф не имеет стоков (матрица не содержит нулевых строк таких, что соответствующие столбцы (с тем же номером, что и нулевая строка)) ненулевые;

3) Орграф не имеет источников (матрица не содержит нулевых столбцов таких, что соответствующие строки (с тем же номером, что и нулевой столбец)) ненулевые;

4) Орграф не имеет изолированных вершин (матрица смежности не содержит нулевых строк и нулевых столбцов с теми же номерами).

5) Орграф не имеет петель (главная диагональ матрицы содержит только нулевые элементы).

6) Орграф не имеет кратных ребер (матрица не содержит отличных от нуля и единицы элементов).

7) Орграф является обыкновенным (не содержит петель и кратных ребер).

8) Для каждой вершины орграфа можно подсчитать полустепени захода и исхода. Для определения полустепени исхода данной вершины необходимо зафиксировать строку с номером, совпадающим с номером вершины, и подсчитать количество 1 в этой строке, а для определения полустепени захода вершины необходимо зафиксировать столбец с номером, совпадающим с номером вершины, и подсчитать количество 1 в этом столбце. Тем самым, можно определить степень вершины. В нашем случае (учитываем deg(v)=deg ^- (v)+deg⁺(v)) имеем:

deg(v₁)=3+4=7; deg(v₂)=3+2=5; deg(v₃)=2+3=5; deg(v₄)=2+3=5;

deg(v₅)=3+2=5, deg(v₆)=4+3=7; deg(v₇)=3+3=6.

9) Если ввести следующую нумерацию ребер орграфа

(v₁, v₂), ( v₁, v₃), ( v₁, v₅), (v₁, v₆), (v₂, v₆), (v₂, v₄), (v₃, v₁), (v₃, v₇), ( v₃, v₅), ( v₄, v₂), (v₄, v₇),

(v₄, v₆), (v₅, v₂), (v₅, v ₁), (v₆, v₃), ( v₆, v₅), ( v₆, v₇), (v₇, v₄), (v₇, v₆),

то матрица инцидентности орграфа следующая:

10) Если ввести следующую нумерацию ребер графа, ассоциированного с исходным орграфом

(v₁, v₂), ( v₁, v₃), ( v₁, v₅), (v₁, v₆), (v₁, v₇), (v₂, v₆), (v₂, v₅), (v₂, v₄), ( v₃, v₇), ( v₃, v₆), (v₃, v₅),

(v₄, v₇), (v₄, v₆), (v₅, v₆), (v₆, v₇),

то матрица инцидентности графа следующая:

Задача 4. Введем следующие нумерации вершин исходных графов

v₁ v₂ v₃ y₁ y₂

G: G’:

y₃ y₄

v₄v₅v₆ y₅y₆

Нетрудно увидеть, что все вершины как первого, так и второго графов имеют одну и ту же степень (три). Поэтому биекцию между множествами вершин установить можно. Поскольку устанавливаемая биекция множеств вершин должна сохранять инцидентность, то сопоставим, например, вершине v₁ вершину y₁, а вершинам v₄, v₅,v₆, смежным с v₁ сопоставим соответственно вершины y₃, y₆, y₂, смежные с y₁. Запишем полученное соответствие в виде подстановки

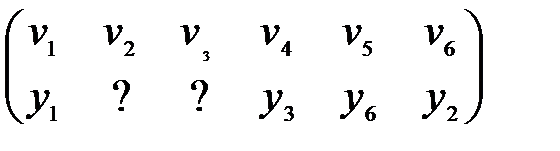
Пока такое соответствие сохраняет инцидентность – ребрам {v₁, v₄}, {v₁, v₅}, {v₁, v₆} отвечают ребра {y₁, y₃}, {y₁, y₆}, {y₁, y₂} соответственно, а попарно несмежным между собой вершинам v₄, v₅, v₆ отвечают попарно несмежные между собой вершины y₃, y₆, y₂. Если сопоставим вершине v₂ вершину y₄, то инцидентность сохранится (ребрам

{v₂, v₄}, {v₂, v₅}, {v₂, v₆} отвечают ребра {y₄, y₃}, {y₄, y₆}, {y₄, y₂}). Остается сопоставить вершине v₃ вершину y₅ и убедиться, что инцидентность сохраняется и в этом случае (v₃ смежная с вершинами v₄, v₅, v₆, а y₅ – с вершинами y₃, y₆, y₂). Таким образом, искомая биекция

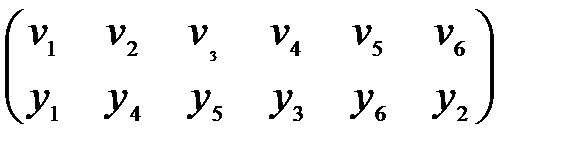
между множествами вершин найдена и, следовательно, исходные графы изоморфны между собой.

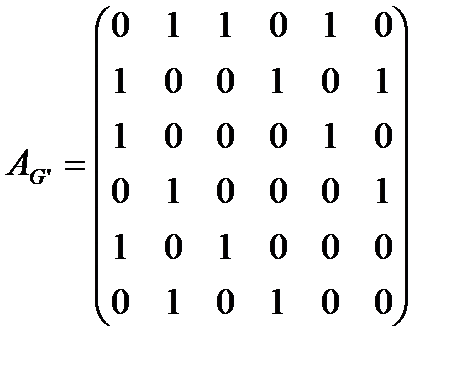
Проведенное выше доказательство изоморфности графов можно оформить с помощью их матриц смежност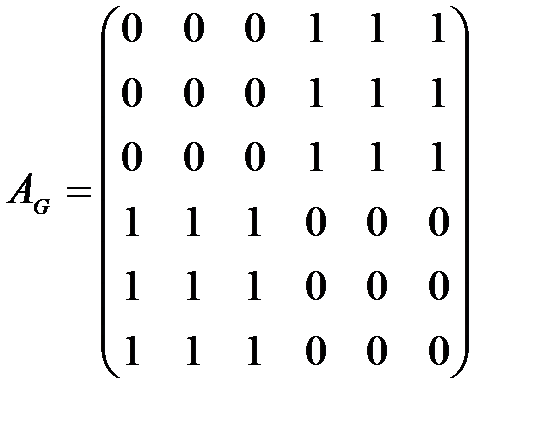и

и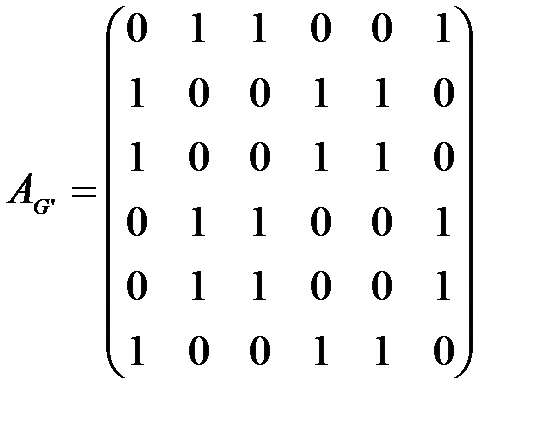

Поменяем во второй матрице 2-ю и 4-ю строки (соответственно 2-й и 4-й столбцы) и 3-ю и 5-ю строки (соответственно 3-й и 5-й столбцы), получим

.

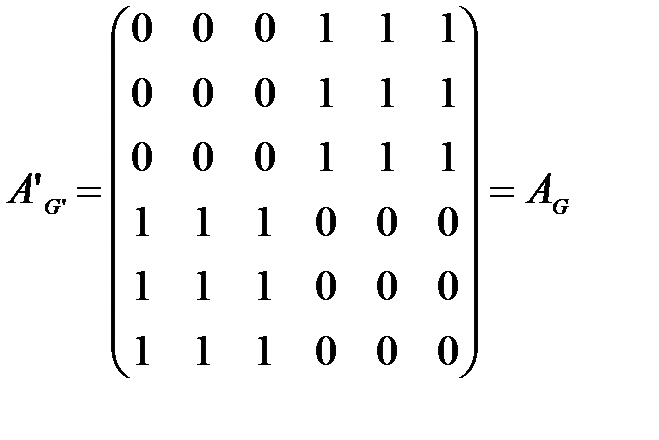Следовательно, в силу теоремы 4.1, графы G и G’ изоморфны. Более того, если вспомнить перестановку строк и столбцов, то в последней матрице

1-я строка (и 1-й столбец) соответствует вершине y₁;

2-я строка (и 2-й столбец) соответствует вершине y₄;

3-я строка (и 3-й столбец) соответствует вершине y₅;

4-я строка (и 4-й столбец) соответствует вершине y₂;

5-я строка (и 5-й столбец) соответствует вершине y₃;

6-я строка (и 6-й столбец) соответствует вершине y₆.

Тем самым найдена еще одна биекция между множествами вершин исходных графов, сохраняющая инцидентность (в чем легко убедиться),

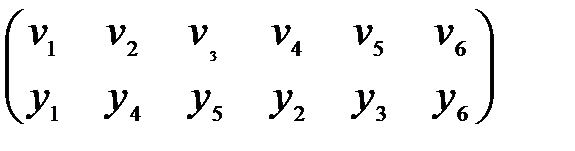
Рекомендуемая литература

Основная литература

1. А.И.Белоусов, С.Б.Ткачев Дискретная математика. М.:МГТУ им.Баумана, 2004.

2. Д.А.Андерсон, Дискретная математика и комбинаторика. М.:Вильямс, 2003.

3. Г.П.Гаврилов, А.А.Сапоженко Сборник задач по дискретной

математике. М.: Наука, 1977.

Дополнительная литература

1. Ф.А.Новиков Дискретная математика для программистов.С-П.:Питер, 2001

2. Ю.Г.Карпов Теория автоматов. М.: Питер, 2002.

Храмцов Н. В. Металлы и сварка (лекционный курс): Учебное пособие. Тюмень: Издательство Тюменского государственного университета, 2001. 160 с.

В учебном пособии, предназначенном для студентов
специальностей ПГС, ПСК и ТГВ, даны основы теории
и практического использования металлов, сплавов и сварки в строительстве.

РЕЦЕНЗЕНТ:

заслуженный строитель России, доктор технических наук, профессор Н. А. Малюшин

ISBN 5–88081–222–7 © Храмцов Н. В., 2001

Человечество с древних времен знакомо с металлами. Орудия труда, хозяйственная утварь и украшения в основном изготовлялись из металла. Освоение материалов шло
в следующей последовательности: камень, золото, серебро, медь (бронза) и железо, поэтому по материалу орудий труда и оружия исторические периоды развития человечества делятся на каменный, бронзовый и железный века. Следовательно, в настоящее время мы живем в веке железа.
Огромны природные ресурсы металлов, так, доля железа (по весу) составляет третью часть всего земного шара,
а в его поверхностном слое (до 1 км) находится 5 % железа, 8 % алюминия, 28 % кремния, 47 % кислорода и только 0,0000005 % золота и 0,00001 % серебра. Разведанных запасов месторождений железа хватит для человечества более чем на два последующих столетия.

На человека в мире приходится в среднем около 4 тонн железа, из которого изготовлены строительные конструкции, трубопроводы, машины, трактора, грузовые и легковые автомобили, бытовые приборы, инструмент и пр. В машинах и строительных конструкциях преобладают детали, изготовленные из стали и чугуна. Более редкие и, как правило, дорогие металлы и сплавы в основном используются
в радиоэлектронике и для украшений.

В связи со столь широким использованием металлов
в нашей практической деятельности чрезвычайно велика роль знаний о металлах, о технологии изготовления и ремонта деталей и конструкций. Человек, знающий металлы
и умеющий их обрабатывать, всегда пользовался уважением и почетом у всех народов мира. Так, единственным «рабочим» богом во многих религиях были кузнецы: Гефест у греков, Сварог у славян, Вулкан у римлян. В Англии многие удачливые кузнецы даже становились лордами.

Старинная легенда рассказывает, что царь Соломон
по окончании строительства Иерусалимского храма (XI век до новой эры) задумал прославить лучших строителей
и пригласить их во дворец, а на время пира уступить свой царский трон лучшему из лучших — тому, кто особенно много сделал для строительства храма. Когда приглашенные явились во дворец, то один из них быстро взошел по ступеням золотого трона и сел на него. Его поступок вызвал изумление у присутствующих.

— Кто ты и по какому праву занял трон? — грозно спросил разгневанный царь.

Незнакомец обратился к каменщику и спросил его:

— Кто сделал твои инструменты?

— Кузнец, — ответил тот.

Сидящий на троне обратился к плотнику, столяру:

— Кто вам сделал инструмент?

— Кузнец, — ответили те.

И все, к кому обращался незнакомец, отвечали:

— Да, кузнец выковал наши инструменты, которыми
и был построен храм.

И царь согласился с доводами, что никто из присутствующих строителей не смог бы выполнить свою работу без сделанных кузнецом инструментов, а сам кузнец заслуживает наибольшего почета среди строителей.

В настоящее время без автомобиля и водителя, без экскаватора и экскаваторщика, без крана и крановщика, без слесаря, токаря, сварщика и других работников, связанных с изготовлением, эксплуатацией и ремонтом машин и металлоконструкций, нельзя представить современную стройку.

Инженер-строитель в своей практической деятельности непрерывно связан с использованием металлов
в строительных конструкциях, с организацией труда рабочих и технологией рационального использования
машин. Чтобы эффективно руководить производством, надо «понимать» металлы и знать основы технологии их обработки, конструкторские особенности машин,
вопросы эксплуатации и ремонта.

Дата добавления: 2014-12-16