Зададим функцию таблично

n:= 11 число значений аргумента

a:= 2 начальное значение аргумента

h:= 0.7 шаг изменения аргумента

i:= 0.. n

x_i:= a + i×h значения аргумента

y_i:= ln(x_i) + rnd(2) значения функции

таблицы значений х и у

	графическое представление заданной функции:

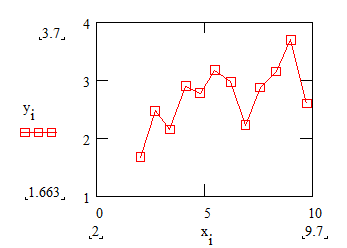
xx:= 6.35 данное значение аргумента

ix:= 6 номер табличного значения аргумента, ближайшего к данному

Найдем угловой коэффициент прямой, проходящей через 2 точки, ближайшие к хх.

j:= ix - 1.. ix + 1

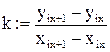
в уравнение искомой прямой подставим значение хх аргумента

yx:= y_ix + k×(xx - x_ix)

yx = 2.812

Проиллюстрируем решение графически:

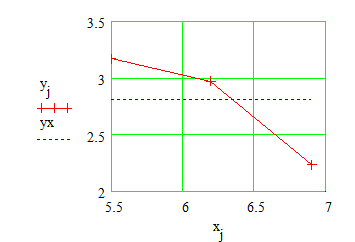
В пакете MathCad имеются встроенные функции, которые позволяют быстрее решить задачу линейной интерполяции. Это выполняется функцией linterp(vx,vy,x), которая использует векторы данных vx и vy, чтобы вычислить линейно интерполируемое значение у, соответствующее третьему аргументу х. Аргументы vx и vy должны быть одинаковой длины. Вектор vx должен содержать вещественные значения, расположенные в порядке возрастания. На рисунке 4 решена предложенная задача линейной интерполяции

.

ЛАБОРАТОРНАЯ РАБОТА №2

Задание: Используя квадратичную интерполяцию, вычислить значения функции у(х), заданной таблично, при заданном значении аргумента.

Образец выполнения задания

Зададим функцию таблично

n:= 11 число значений аргумента

a:= 2 начальное значение аргумента

h:= 0.7 шаг изменения аргумента

i:= 0.. n

x_i:= a + i×h + rnd(0.8) значения аргумента

y_i:= ln(x_i) + rnd(2) значения функции

таблицы значений х и у

графическое представление заданной функции

xx:= 7.575 данное значение аргумента

ix:= 7 номер табличного значения аргумента,

ближайшего к данному

Через 3 точки, ближайшие к хх (х₇, х₈, х₉) проведем параболу y(x)=ax²+bx+c, коэффициенты которой найдем по формуле:

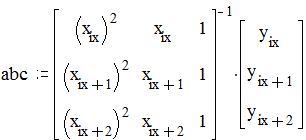
f(t):= abc₀×t² + abc₁×t + abc₂ Уравнение искомой параболы

yx:= f(xx) в найденное уравнение подставим

значение хх аргумента

yx = 2.806

Проиллюстрируем решение графически

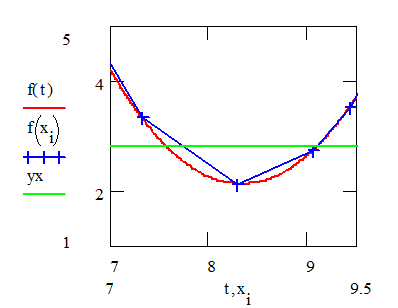
В пакете MathCad имеются встроенные функции, которые позволяют быстрее решить задачу квадратичной интерполяции. На рисунке 5 предлагается решение данной задачи.

Дата добавления: 2014-12-16