У основі чисельного методу розв’язування системи лінійних рівнянь лежить теорема про перетворення системи лінійних рівнянь

Метод Жордана-Гауса

Системи лінійних рівнянь

Лекція 2

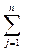Оскільки у більшості методів розв’язування задачі лінійного програмування використовується канонічна форма, що являє собою систему рівнянь для невід’ємних змінних, розглянемо властивості систем лінійних рівнянь. Систему лінійних рівнянь можна уявити у вигляді

а_ijх_j = b_i, i = 1, m,

або у матричній формі Ах = b, де матриця коефіцієнтів А = ||а_ij||_i,j=1^m,n.

Розв’язком системи називається сукупність значень змінних х₁ = d₁, х₂ = d₂, …, х_n = d_n, яка задовільняє усім рівнянням системи. Система, що має хоча б один розв’язок називається сумісною, а система, що не має жодного розв’язку називається несумісною. Сумісна система, що має тільки один рзв’язок називається визначеною. Система що має більше одного розв’язку називається невизначеною. Дві системи називаються рівносильними, якщо множини їх розв’язків співпадають. Під розв’язуванням системи лінійних рівнянь розуміють визначення множини усіх розв’язків системи.

Теорема 2.1. Якщо і-те рівняння системи замінити сумою цього рівняння з j-м рівнянням, помноженим на дійсне число t, то отримана система рівносильна вихідній.

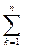Доведення. Нехай d = (d₁, d₂, …, d_n) - розв’язок вихідної ситеми. Це означає, що

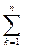а_ikd_k = b_i,

а_jkd_k = b_j.

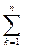
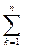
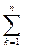Помноживши друге числове рівняння на число t і додавши добуток до першого, отримуємо

а_ikd_k + tа_jkd_k = b_i + tb_j = (а_ik + tа_jk)d_k.

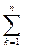Звідси маємо, що d задовольняє рівнянню

(а_ik + tа_jk)x_k = b_i + tb_j,

і тому є розв’язком нової системи.

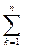Тепер припустимо, що d = (d₁, d₂, …, d_n) - розв’язок нової системи. Це означає, що мають місце такі числові рівняння

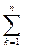(а_ik + tа_jk)d_k = b_i + tb_j,

а_jkd_k = b_j.

Помноживши друге рівняння на -t і додавши добуток до першого, переконуємося, що d задовольняє і-му рівнянню вихідної системи і є її розв’язком.

Чисельний метод розв’язування системи рівнянь, що далі розглядається, називається методом повного вилучення змінних або методом Жордана-Гауса.

Ідея методу полягає у багаторазовому переході від поточної системи до рівносильної з метою отримання такої системи, розв’язок якої визначається очевидним чином.

Метод являє собою ітераційну процедуру, на і-й ітерації розглядається і-те рівняння поточної системи. У і-му рівнянні визначається ненульовий коефіцієнт а^’_ij при деякій змінній х_j. Мета перетворення системи на і-й ітерації полягає в тому, щоб у рівносильній системі у і-тому рівнянні отримати при змінній х_j коефіцієнт, що дорівнює одиниці, а в усіх інших рівняннях при цій змінній отримати нульовий коефіцієнт (вилучити змінну х_j з усіх рівнянь, крім і-того). Визначений коефіцієнт а^’_ij називають ведучим елементом. У матриці коефіцієнтів системи рівнянь рядок та стовпчик, що містять ведучий елемент, називать відповідно ведучим рядком та ведучим стовпчиком.

Для того, щоб отримати у ведучому рядку одиничний коефіцієнт при х_j, треба поділити ведучий рядок на ведучий елемент. Нові значення коефіцієнтів ведучого рядка визначаються формулою

а^’’_is = а^’_is / а^’_ij, s = 1, n. (2.1)

Нові значення коефіцієнтів інших рядків визначаються умовою нульового нового значення коефіцієнта при змінній х_j. Для того, щоб виконати цю умову у довільному рядку r, треба перетворений ведучий рядок помножити на старе значення кофіцієнту у рядку r при х_j і результат відняти від цього рядка. Формула обчислення нового значення коефіцієнта має вигляд

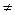
а^’’_rs = а^’_rs - а^’_is а^’_rj / а^’_ij, s = 1, n; r i. (2.2)

Аналогічно перетворюються і праві частини рівнянь

b^’’_i = b^’_i / а^’_ij; (2.3)

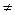b^’’_r = b^’_r - b^’_i а^’_rj / а^’_ij, s = 1, n; r i. (2.4)

Перетворення матриці коефіцієнтів системи рівнянь за формулами (2.1) – (2.4) називається симплексним перетворенням.

Якщо при виконанні поточної ітерації виявляється, що рядок коефіцієнтів не містить жодного ненульового елемента, тобто відповідне рівняння має вигляд 0х₁ + 0х₂ + … + 0x_n = b^’_i, то відрізняють два випадки.

1. b^’_i = 0. У цьому випадку рівняння задовольняється при будь-якому наборі значень змінних х₁, х₂, …, x_n, і тому рівняння вилучається без втрати рівносильності.

2. 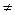b^’_i 0. У цьому випадку рівняння не задовольняється при жодному наборі значень змінних х₁, х₂, …, x_n, і тому поточна система рівнянь не сумісна. Оскільки ця система рівносильна вихідній (на кожній ітерації відбувається перехід до рівносильної системи), то і вихідна система не сумісна.

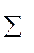
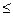Якщо система сумісна то у результаті застосування метода Жордана-Гауса утворюється система m^* рівнянь (m^* m, де m - кількість рівнянь у вихідній системі). Кожне i-те рівняння має одну змінну х^’_i, що вилучена з усіх інших рівнянь. Ці змінні називаються базисними, усі інші змінні – небазисними. Якщо множину індексів небазисних змінних позначити як N, то отриману систему можна уявити у вигляді

х^’_i + a_ij х_j = b^’_i, i = 1, m^*.

j N

Розв’язавши отриману систему відносно базисних змінних, отримуємо загальний розв’язок системи.

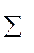х^’_i = b^’_i - a_ij х_j, i = 1, m^*. (2.5)

j N

Присвоюючи довільні значення небазисним змінним можна отримати відповідні значення базисних змінних Це дає змогу отримати усі сукупності значень змінних, що задовольняють системі рівнянь, тобто усі розв’язки системи. Саме тому систему (2.5) і називають загальним розв’язком.

Розв’язок, що відповідає конкретним значенням змінних, називається частинним. Частинний розв’язок, у якого усі небазисні змінні дорівнюють нулю, називається базисним розв’язком.

Дата добавления: 2014-12-16