Виды информации

Источники Маркова.

Источники Бернулли.

Моделирование источников информации

Для создания оптимального архиватора недостаточно быть хорошим программистом и разобрать дюжину известных алгоритмов. Необходимо правильно оценить модель источника сигнала, которой подчиняются входные сообщения и выбрать тот алгоритм, который разрабатывался на основе этой модели. Неправильно выбранная модель сигнала может привести к тому, что “хороший” архиватор откажется сжимать входную информацию, хотя она будет достаточно избыточной. Несмотря на разнообразие различных сигналов в основу их анализа положено всего две основные вероятностные модели: модель источника сигнала Бернулли и Маркова.

Сигнал порождается источником Бернулли, если очередное сообщение или код не зависит от всех предыдущих, иными словами все сообщения независимы и характеризуются только своими вероятностями. Примером являются, например, результаты бросания монеты или игрального кубика. Результат бросания кубика - сигнал с равными вероятностями всех событий.

Если же на кубик нанести числа 1, 2, 2, 3, 3, 3, то мы получим прекрасный источник не равновероятных сообщений Бернулли. Если в ансамбле сообщений соблюдается одно из двух правил:

p(x_i) ³ p(x_j) для любого i > j или p(x_i) £ p(x_j) для любого i > j,

то такой источник называется монотонным.

Источник Маркова - более сложная модель. В ней предполагается, что вероятность появления очередного символа зависит от n предыдущих. Соответственно получается источник сигнала Маркова n-го порядка. Чем больше n, тем сложнее учет и оценка зависимостей, поэтому на практике ограничиваются значением n = 1..2. Очевидно, что модель Бернулли-это модель Маркова при n=0.

Если для источника Бернулли необходимо знать только вероятности отдельных сообщений, то для источника Маркова необходимо получить условные вероятности в виде n+1-мерных матриц. Для марковского источника первого порядка это будет двумерная матрица размера LxL, где каждый i-й столбец показывает вероятность перехода от сообщения x_i к сообщению x_j, например:

	x1	...	xi-1	xi	xi+1	...	xL
x1	p1,1	...	...	p1,i	...	...	p1,L
...	...	...	...	...	...	...	...
xj-1	pj-1,1	...	...	pj-1,i	...	...	pj-1,L
xj	pj,1	...	...	pj,i	...	...	pj,L
xj+1	pj+1,1	...	...	pj+1,i	...	...	pj+1,L
...	...	...	...	...	...	...	...
xL	pL,1	...	...	pL,i	...	...	pL,L

Сумма вероятностей любой строки или столбца должна равняться единице.

Примером источника Маркова являются тексты русского (или, например, английского языка). Вероятность появления в слове очередной буквы очень сильно зависит от предыдущих букв или даже слов.

В зависимости от того, какой модели источника сигнала подчиняется информация, ее удобно разбить на несколько видов:

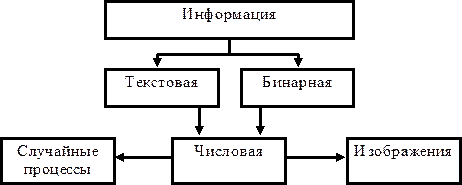
Бинарная информация (исполняемые файлы, программные библиотеки и т.д.) наиболее близко описываются моделью Бернулли и Маркова малых порядков, в то время, как текстовая информация ближе к моделям Маркова высоких порядков. Частным случаем текстовой или бинарной информации являются числовые данные (в зависимости от того, в каком виде они представлены-ASCII или двоичном). Особое положение среди числовых данных занимают изображения (двумерные числовые массивы, описываемые моделями Маркова невысоких порядков) и аналогичные одномерные массивы, представляющие собой временную последовательность значений какого-нибудь процесса (измерительного сигнала, звукового сопровождения и т.д.). Изображения выделены в особую группу еще и потому, что они любят занимать особенно много памяти, требуют при этом высокой скорости обработки и, к счастью, часто допускают сжатие с потерями.

3 Алгоритмы сжатия двоичной информации

Дата добавления: 2014-12-16