Код Хаффмана

Унарное кодирование

Один из очевидных способов сжатия информации, в особенности текстовой, основывается на том, что вероятность использования в тексте разных символов сильно различна. В частности, в русском языке чаще всего используются буквы “о”, “а”, редко-“ъ”,”щ” и т.д. Поэтому, предлагается использовать для частых символов более короткий код, для редких – более длинный. Трудность заключается в том, что коды получаются переменной длины и в общем потоке выходных данных трудно обнаружить конец одного кода и начало другого.

Однако, существуют коды, для которых задача определения длины легко решается к таким кодам относятся так называемые неравномерные коды со свойством однозначного декодирования. Например, унарный код (в двоичной системе), где:

“о”-1

“а”-01

“и”-001

...

“щ”-00....1

т.е. для самой частой буквы длина кода составляет 1 бит, для самой редкой-33 бита (32 нуля и единица). Этот код очень прост, но далеко не эффективен. Но еще может нам пригодиться для построения кодов целых переменной длины (Variable Length Integers (VLI) codes). Именно эти коды с успехом применяются в архиваторах ARJ и LHA. VLI-коды состоят из двух частей: сначала следует унарный код, определяющий группу чисел определенной длины, а затем само число указанной длины. Таким образом, унарный код выполняет роль префикса, указывающего – какой длины будет следующее число. Для записи VLI-кодов используют три числа: (start, step, stop), где start определяет начальную длину числа, step -приращение длины для следующей группы, stop -конечную длину.

Например: код (3, 2, 9) задает четыре группы чисел:

0ххх - числа от 0 до 7, группа 0,

10ххххх - числа от 8 до 39, группа 1,

110ххххххх - числа от 40 до 167, группа 2,

111ххххххххх - числа от 168 до 679, группа 3.

Унарный код для n-ой группы – n единиц, затем ноль; для последней группы-только n единиц, так как это не вносит неопределенности. Размер числа из n-ой группы равен start + n× step. VLI-коды удобно применять для кодирования монотонных источников, для которых вероятность появления меньших чисел выше, чем больших. При отсутствии кодирования любое число представлялось бы десятью битами.

Идея, лежащая в основе кода Хаффмана, достаточно проста. Вместо того чтобы кодировать все символы одинаковым числом бит (как это сделано, например, в ASCII кодировке, где на каждый символ отводится ровно по 8 бит), будем кодировать символы, которые встречаются чаще, меньшим числом бит, чем те, которые встречаются реже.

Алгоритм был опубликован Дэвидом Хаффманом (David Huffman) в 1952 году, и за прошедшие 50 лет со дня опубликования, код Хаффмана ничуть не потерял своей актуальности и значимости. Данный алгоритм и сейчас активно используется различными архиваторами.

Алгоритм Хаффмана двухпроходный. На первом проходе строится частотный словарь и генерируются коды, на втором проходе происходит непосредственно кодирование.

Определение 1: Пусть A={a₁,a₂,_...,a_n} - алфавит из n различных символов, W={w₁,w₂,_...,w_n} - соответствующий ему набор положительных целых весов. Тогда набор бинарных кодов C={c₁,c₂,_...,c_n}, такой что:

1. c_i не является префиксом для c_j, при i ¹ j.

2. 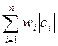минимальна (|c_i| длина кода c_i).

называется минимально-избыточным префиксным кодом или иначе кодом Хаффмана.

Замечания:

1. Свойство (1) называется свойством префиксности. Оно позволяет однозначно декодировать коды переменной длины.

1. Сумму в свойстве (2) можно трактовать как размер закодированных данных в битах. На практике это очень удобно, т.к. позволяет оценить степень сжатия не прибегая непосредственно к кодированию.

Известно, что любому бинарному префиксному коду соответствует определенное бинарное дерево.

Определение 2: Бинарное дерево, соответствующее коду Хаффмана, будем называть деревом Хаффмана.

Задача построения кода Хаффмана равносильна задаче построения соответствующего ему дерева. Приведем общую схему построения дерева Хаффмана:

1. Составим список кодируемых символов.
2. Из списка выберем 2 узла (элемента) с наименьшим весом.
3. Сформируем новый узел и присоединим к нему, в качестве дочерних, два узла выбранных из списка. При этом вес сформированного узла положим равным сумме весов дочерних узлов.
4. Добавим сформированный узел к списку.
5. Если в списке больше одного узла, то повторить 2-5.

Приведем пример: построим дерево Хаффмана для сообщения

S="A H F B H C E H E H C E A H D C E E H H H C H H H D E G H G G E H C H H".

Для начала введем несколько обозначений:

1. Веса узлов будем обозначать нижними индексами: A ₅, B ₃, C ₇.
2. Составные узлы будем заключать в скобки: ((A ₅+ B ₃)₈+ C ₇)₁₅.

Итак, в нашем случае A={ A, B, C, D, E, F, G, H }, W={2, 1, 5, 2, 7, 1, 3, 15}.

1. A ₂ B ₁ C ₅ D ₂ E ₇ F ₁ G ₃ H ₁₅
2. A ₂ C ₅ D ₂ E ₇ G ₃ H ₁₅ (F ₁+ B ₁)₂
3. C ₅ E ₇ G ₃ H ₁₅ (F ₁+ B ₁)₂ (A ₂+ D ₂)₄
4. C ₅ E ₇ H ₁₅ (A ₂+ D ₂)₄ ((F ₁+ B ₁)₂+ G ₃)₅
5. E ₇ H ₁₅ ((F ₁+ B ₁)₂+ G ₃)₅ (C ₅+(A ₂+ D ₂)₄)₉
6. H ₁₅ (C ₅+(A ₂+ D ₂)₄)₉ (((F ₁+ B ₁)₂+ G ₃) ₅+ E ₇)₁₂
7. H ₁₅ ((C ₅+(A ₂+ D ₂)₄) ₉+(((F ₁+ B ₁)₂+ G ₃) ₅+ E ₇)₁₂)₂₁
8. (((C ₅+(A ₂+ D ₂)₄) ₉+(((F ₁+ B ₁)₂+ G ₃) ₅+ E ₇)₁₂)₂₁+ H ₁₅)₃₆

В списке, как и требовалось, остался всего один узел. Дерево Хаффмана построено. Теперь запишем его в более привычном для нас виде.

ROOT /\ 0 1 / \ /\ H / \ / \ / \ 0 1 / \ / \ / \ / \ /\ /\ 0 1 0 1 / \ / \ C /\ /\ E 0 1 0 1 / \ / \ A D /\ G 0 1 / \ F B

Листовые узлы дерева Хаффмана соответствуют символам кодируемого алфавита. Глубина листовых узлов равна длине кода соответствующих символов.

Путь от корня дерева к листовому узлу можно представить в виде битовой строки, в которой "0" соответствует выбору левого поддерева, а "1" - правого. Используя этот механизм, мы без труда можем присвоить коды всем символам кодируемого алфавита. Выпишем, к примеру, коды для всех символов в нашем примере:

A=0010bin	C=000bin	E=011bin	G=0101bin
B=01001bin	D=0011bin	F=01000bin	H=1bin

Теперь у нас есть все необходимое для того чтобы закодировать сообщение S. Достаточно просто заменить каждый символ соответствующим ему кодом:

S^/="0010 1 01000 01001 1 000 011 1 011 1 000 011 0010 1 0011 000 011 011 1 1 1 000 1 1 1 0011 011 0101 1 0101 0101 011 1 000 1 1".

Оценим теперь степень сжатия. В исходном сообщении S было 36 символов, на каждый из которых отводилось по élog₂|A|ù = 3 бита. Таким образом, размер S равен 36*3=108 бит

Размер закодированного сообщения S^/ можно получить воспользовавшись замечанием 2 к определению 1, или непосредственно, подсчитав количество бит в S^/. И в том и другом случае мы получим 89 бит.

Алгоритм декодирования: Начиная с корня дерева двигаться вниз, выбирая левое поддерево, если очередной бит в потоке равен "0", и правое - если "1". Дойдя до листового узла декодируем соответствующий ему символ.

Дата добавления: 2014-12-16