Арифметическое кодирование

Метод Хаффмана является простым и эффективным, однако, он порождает наилучшие коды переменной длины (коды, у которых средняя длина равна энтропии алфавита) только когда вероятности символов алфавита являются степенями числа 2, то есть равны 1/2, 1/4, 1/8 и т.п. Это связано с тем, что метод Хаффмана присваивает каждому символу алфавита код с целым числом битов. Теория информации предсказывает, что при вероятности символа, скажем, 0.4, ему в идеале следует присвоить код длины 1.32 бита, поскольку 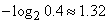. А метод Хаффмана присвоит этому символу код длины 1 или 2 бита.

Арифметическое кодирование решает эту проблему путем присвоения кода всему, обычно, большому передаваемому файлу вместо кодирования отдельных символов. (Входным файлом может быть текст, изображение или данные любого вида.) Алгоритм читает входной файл символ за символом и добавляет биты к сжатому файлу. Чтобы понять метод, полезно представлять себе получающийся код в виде числа из полуинтервала 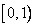. Таким образом, код «9746509» следует интерпретировать как число «0.9746509» однако часть «0.» не будет включена в передаваемый файл.

На первом этапе следует вычислить или, по крайней мере, оценить частоты возникновения каждого символа алфавита. Наилучшего результата можно добиться, прочитав весь входной файл на первом проходе алгоритма сжатия, состоящего из двух проходов. Однако, если программа может получить хорошие оценки частот символов из другого источника, первый проход можно опустить.

В первом примере мы рассмотрим три символа 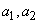и 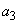с вероятностям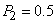и , и 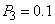, соответственно. Интервал 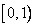делится между этими тремя символами на части пропорционально их вероятностям. Порядок следования этих подынтервалов не существенен. В нашем примере трем символам будут соответствовать подынтервалы 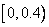, 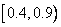и 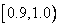. Чтобы закодировать строку «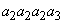», мы начинаем с интервала 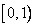. Первый символ 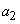сокращает этот интервал, отбросив от него 40% в начале и 10% в конце. Результатом будет интервал 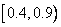. Второй символ 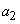сокращает интервал 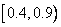в той же пропорции до интервала 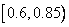. Третий символ 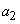переводит его в 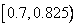. Наконец, символ 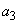отбрасывает от него 90% в начале, а конечную точку оставляет без изменения. Получается интервал 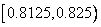. Окончательным кодом нашего метода может служить любое число из этого промежутка. (Заметим, что подынтервал 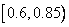получен из 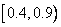с помощью следующих преобразований его концов: 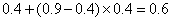и ).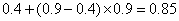

На этом примере легко понять следующие шаги алгоритма арифметического кодирования:

1. Задать «текущий интервал» .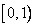

2. Повторить следующие действия для каждого символа 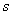входного файла.

2.1. Разделить текущий интервал на части пропорционально вероятностям каждого символа.

2.2. Выбрать подынтервал, соответствующий символу 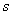, и назначить его новым текущим интервалом.

3. Когда весь входной файл будет обработан, выходом алгоритма объявляется любая точка, которая однозначно определяет текущий интервал.

После каждого обработанного символа текущий интервал становится все меньше, поэтому требуется все больше бит, чтобы выразить его, однако окончательным выходом алгоритма является единственное число, которое не является объединением индивидуальных кодов последовательности входных символов. Среднюю длину кода можно найти, разделив размер выхода (в битах) на размер входа (в символах).

Следующий пример будет немного более запутанным. Мы продемонстрируем шаги сжатия для строки «SWISS_MISS». В таблице ниже указана информация, приготовленная на предварительном этапе (статистическая модель данных). Пять символов на входе можно упорядочить любым способом. Для каждого символа сначала вычислена его частота, затем найдена вероятность ее появления (частота, деленная на длину строки, 10). Область 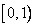делится между символами в любом порядке. Каждый символ получает кусочек или подобласть, равную его вероятности. Таким образом, символ «S» получает интервал 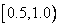длины 0.5, а символу «I» достается интервал 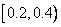длины 0.2. Столбец CumFreq (накопленные частоты) будет использоваться алгоритмом декодирования на стр. 71. CumFreq равно сумме частот всех предыдущих символов, например, для «W», .

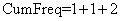Символ	Частота	Вероятность	Область	CumFreq
Общая CumFreq =
S		5/10=0.5	[0.5,1.0)
		1/10=0.1	(0.4,0.5)
I		2/10=0.2	[0.2,0.4)
N		1/10=0.1	[0.1,0.2)
-		1/10=0.1	(0.0,0.1)

Символы и частоты записываются в начало выходного файла до битов кода сжатия.

Процесс кодирования начинается инициализацией двух переменных Low и High и присвоением им 0 и 1, соответственно. Они определяют интервал 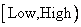. По мере поступления и обработки символов, переменные Low и High начинают сближаться, уменьшая интервал.

После обработки первого символа «S», переменные Low и High равны 0.5 и 1, соответственно. Окончательным сжатым кодом всего входного файла будет число из этого интервала 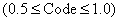. Для лучшего понимания процесса кодирования хорошо представить себе, что новый интервал 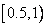делится между пятью символами нашего алфавита в той же пропорции, что и начальный интервал 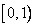. Результатом будет пять подынтервалов , , 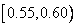, 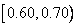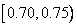и 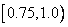. После поступления следующего символа «V» выбирается четвертый интервал, который снова делится на пять подынтервалов.

Символ		Вычисление переменных Low и High
S	L	0.0 + (1.0 – 0.0) × 0.5	=	0.5
	Н	0.0 + (1.0 – 0.0) × 1.0	=	1.0
W	L	0.5 + (1.0 – 0.5) × 0.4	=	0.70
	Н	0.5 + (1.0 – 0.5) × 0.5	=	0.75
I	L	0.7 + (0.75 – 0.70) × 0.2	=	0.71
	Н	0.7 + (0.75 – 0.70) × 0.4	=	0.72
S	L	0.71 + (0.72 – 0.71) × 0.5	=	0.715
	Н	0.71 + (0.72 – 0.71) × 1.0	=	0.72
S	L	0.715 + (0.72 – 0.715) × 0.5	=	0.7175
	Н	0.715 + (0.72 – 0.715) × 1.0	=	0.72
-	L	0.7175 + (0.72 – 0.7175) × 0.0	=	0.7175
	Н	0.7175 + (0.72 – 0.7175) × 0.1	=	0.71775
М	L	0.7175 + (0.71775 – 0.7175) × 0.1	=	0.717525
	Н	0.7175 + (0.71775 – 0.7175) × 0.2	=	0.717550
I	L	0.717525 + (0.71755 – 0.717525) × 0.2	=	0.717530
	Н	0.717525 + (0.71755 – 0.717525) × 0.4	=	0.717535
S	L	0.717530 + (0.717535 – 0.717530) × 0.5	=	0.7175325
	Н	0.717530 + (0.717535 – 0.717530) × 1.0	=	0.717535
S	L	0.7175325 + (0.717535 – 0.7175325) × 0.5	=	0.71753375
	Н	0.7175325 + (0.717535 – 0.7175325) × 1.0	=	0.717535

С каждым поступившим символом переменные Low и High пересчитываются по правилу:

;

;

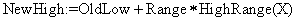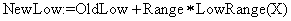где 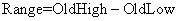, a HighRange(X) и LowRange(X) обозначают верхний и нижний конец области символа X. В нашем примере второй символ это «W», поэтому новые переменные будут 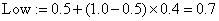, 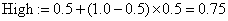. Новый интервал 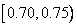покрывает кусок 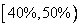подобласти символа «S». В табл. 1.25 приведены все шаги, связанные с кодированием строки «SWISS_MISS». Конечный код - это последнее значение переменной Low, равное 0.71753375, из которого следует взять лишь восемь цифр 71753375 для записи в сжатый файл (другой выбор кода будет обсуждаться позже).

Декодер работает в обратном порядке. Сначала он узнаёт символы алфавита и считывает данные таблицы частот. Затем он читает цифру «7» и узнаёт, что весь код имеет вид 0.7... Это число лежит внутри интервала 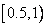символа «S». Значит, первый символ был S. Далее декодер удаляет эффект символа S из кода с помощью вычитания нижнего конца интервала S и деления на длину этого интервала, равную 0.5. Результатом будет число 0.4350675, которое говорит декодеру, что второй символ был «W» (поскольку область «W» - ).

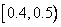Чтобы удалить влияние символа X, декодер делает следующее преобразование над кодом: 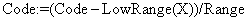, где Range обозначает длину интервала символа X. Процесс декодирования рассмотренной строки:

Символ	Code-Low		Область
S	0.71753375 – 0.5	= 0.21753375	/ 0.5 = 0.4350675
W	0.4350675 – 0.4	= 0.0350675	/ 0.1 = 0.350675
I	0.350675 – 0.2	= 0.150675	/ 0.2 = 0.753375
S	0.753375 – 0.5	= 0.253375	/ 0.5 = 0.50675
S	0.50675 – 0.5	= 0.00675	/ 0.5 = 0.0135
-	0.0135 – 0	= 0.0135	/ 0.1 = 0.135
M	0.135 – 0.1	= 0.035	/ 0.1 = 0.35
I	0.35 – 0.2	= 0.15	/ 0.2 = 0.75
S	0.75 – 0.5	= 0.25	/ 0.5 = 0.5
S	0.5 – 0.5	= 0	/ 0.5 = 0

Дата добавления: 2014-12-16