Импульсных системах

Построение графика переходного процесса в

ОЦЕНКА КАЧЕСТВА ИМПУЛЬСНЫХ СИСТЕМ

Критерий Найквиста.

Импульсная система устойчива, если годограф Найквиста

при изменении частоты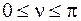

не охватывает точку с координатами .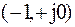

Оценка качества импульсных систем включает в себя определение ошибок системы и расчет ординат переходного

процесса.

1) Вычисление ошибок:

Пусть имеется импульсная система:

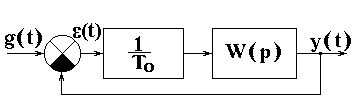
Решетчатая функция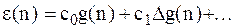

где - коэффициенты ошибки.

,

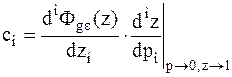Пример 1:

,

, где .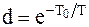

.

,

, ,

.

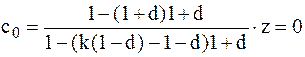
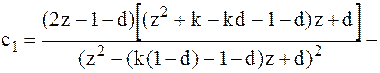
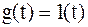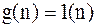Пример 2:

при .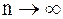

,

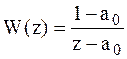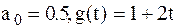
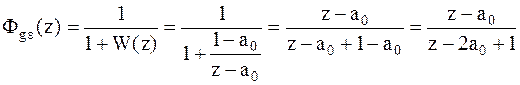
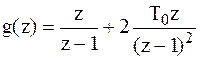
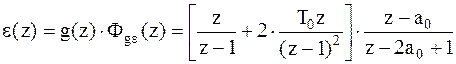
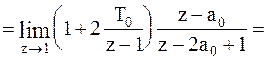
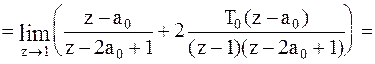
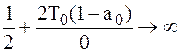
Для расчета решетчатой функции выходного сигнала

системы необходимо найти преобразование сигнала как произведение преобразования входного сигнала на соответствующую передаточную функцию замкнутой системы.

Ординаты выходного сигнала определяются путем разложения изображения выходного сигнала в ряд Лорана по степеням . Разложение в ряд Лорана осуществляется путем деления числителя на знаменатель как многочлена на многочлен, записанных по убывающим степеням 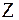. В результате 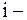ая ордината выходного сигнала равна коэффициенту при 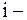ом члене ряда Лорана, т.е. при .

Пример:

1)

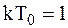
2)

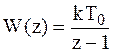
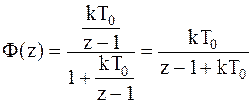
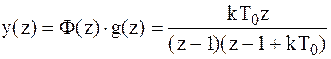
1)

,

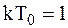
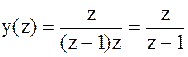Для нахождения промежуточных значений переходной

функции в общем случае, когда непрерывная часть не является интегрирующим звеном, необходимо применять

модифицированное преобразование, то есть находить .

2)

,

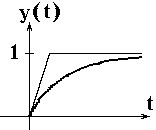
Дата добавления: 2014-12-16