Методы вычислений

Математическая модель

Выходная информация

Отражается, что и в каком виде должно быть получено в результате решения задачи.

Перечень и описание выходных сообщений.

Здесь указываются: • наименования выходных сообщений (документов); • условные обозначения (коды сообщений); • периодичность и сроки выдачи; • количество экземпляров; • получатели выходной информации.

Математическая модель – это приближенное описание какого-либо класса явлений внешнего мира, выраженное с помощью математических символов.

Например: f=-ma, S=gt²/2 и т.д.

Если задача не имеет математической формулировки ее решения, исполь­зуется описание логики последовательных действий в виде выполняемых функ­ций обработки информации по задаче. Математическая или логическая модель решения задачи описывается с достаточной степенью детализации, чтобы в даль­нейшем по модели можно было составить алгоритм и программу решения задачи.

Наиболее часто используются следующие классы моделей формализованного описания постановок задач:

• аналитические (вычислительные) модели; • матричные (балансовые) модели; • графические модели.

Методы вычислений - способы вычислений той или иной величины в соответствии с математическими соотношениями, входящими в математическую модель.

Все вычислительные методы можно разбить на 4 группы:

а) качественные, б) аналитические, в) методы возмущений, г) численные методы.

Качественные методы - методы, которые не дают способ непосредственного вычисления искомой величины, а позволяют определить только саму возможность проведения вычислений и параметры, которые характеризуют процесс вычислений.

Пример: теорема Ферма - всякий многочлен степени n>1 имеет n корней, считая корень столько раз, какова его кратность.

Аналитические методы - методы, позволяющие в принципе сколь угодно точно определить значение искомой величины.

Пример - решение квадратного уравнения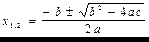

Методы возмущений - это вид аналитических методов, позволяющих приближенно провести вычисления, применяя соотношения, отличающиеся от решаемого аналитическим методом на элемент с малым параметром.

Пример: 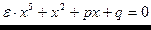(квадратное уравнение + элемент с малым параметром).

Численные методы - методы вычислений, которые сводятся или могут быть сведены к простым арифметическим операциям.

Пример: 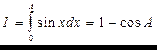- это аналитический метод.

В случае численного метода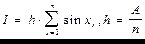

Здесь интегрирование представляет собой сумму произведений.

Для задач, имеющих экономико-математическое описание, обычно выбирается метод ре­шения, который должен обеспечить: необходимую точность расчетов; эффектив­ное решение задачи; программную поддержку (метод - ориентированные ППП, стандартные подпрограммы, встроенные функции и т. п.). Операндами математических формул являются идентификаторы реквизитов входной и выходной информации. Поскольку математическая модель является приближенным отражением реального объекта или процесса, обычно приводит­ся перечень принятых допущений и оценки соответствия принятой модели реаль­ному объекту или процессу в различных режимах и условиях работы (например, аварийные ситуации и т. д.).

Дата добавления: 2014-12-16