Игры с выпуклыми функциями выигрышей

Игры с выпуклыми непрерывными функциями выигрышей, называемые часто ядром, называются выпуклыми.

Напомним, что выпуклой функцией f действительной переменной х на интервале (а,b) называется такая функция, для которой выполняется неравенство

f (a₁ х₁ + a₂ х₂) £ a₁ f (х₁) + a₂ f (х₂),

где х₁ и х₂ – любые две точки из интервала (а,b); a₁, a₂ ³ 0, причём a₁ + a₂ = 1.

Если для a₁ ¹ 0, a₂ ¹ 0 всегда имеет место строгое неравенство

f (a₁ х₁ + a₂ х₂) < a₁ f (х₁) + a₂ f (х₂),

то функция f называется строго выпуклой на (а;b). Геометрически выпуклая функция изображает дугу, график которой расположен ниже стягивающей её хорды (см. рис.)

·

·

·

F(x)

x₂

x₁

x

b

a

a₁ х₁ + a₂ х₂

Напомним, также, что непрерывная и строго выпуклая функция f на замкнутом интервале принимает минимальное значение только в одной точке интервала.

Для нахождения решения выпуклой игры можно воспользоваться следующей теоремой.

Теорема 4. Пусть М (х, y) – непрерывная функция выигрышей игрока 1, на единичном квадрате и строго выпуклая по y для любого х. Тогда имеется единственная оптимальная чистая стратегия y = y_o Î[0;1] для игрока 2, цена игры определяется по формуле

V = 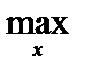M (x, y),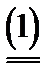

значение y_o определяется как решение следующего уравнения

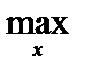M (x, y_o) = V.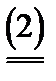

Замечание. Если в теореме 4 не предполагать строгую выпуклость функции М (х, y) по y, а просто выпуклость, то теорема остаётся в силе с тем отличием, что у игрока 2 оптимальная чистая стратегия не будет единственной.

Замечание. Выпуклые игры называют часто выпукло-вогнутыми, т.к. игра в них имеет седлообразное ядро, а так как ядро седлообразное, то игра имеет седловую точку в чистых стратегиях.

Таким образом, если М (х, y) непрерывна и выпукла по y, то цена игры определяется по формуле (1), и игрок 2 имеет оптимальную чистую стратегию, определяемую из уравнения (2).

Аналогично и для игрока 1: если функция выигрышей М (х, y) непрерывна по обоим аргументам и строго вогнута по х при любом y, то в этом случае игрок 1 имеет единственную оптимальную стратегию.

Цена игры определяется по формуле

V = 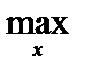M(x,y),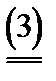

а чистая оптимальная стратегия х_o игрока 1 определяется из уравнения

M (x_o, y) = V.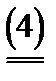

Пример. Пусть на квадрате [0;1] задана функция

М (х, y) = .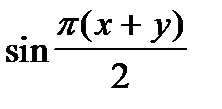

Так как

для x Î[0; 1], y Î(0;1),

то М (х, y) строго вогнута по х для любого y Î(0;1). Следовательно, цена игры находится по формуле (3)

V = .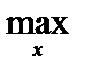

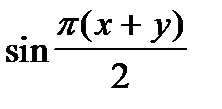Отметим, что при 0 £ х £ справедливо равенство

=

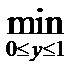
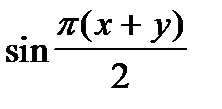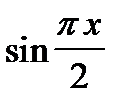
а при 0,5 < х £ 1

=

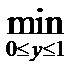
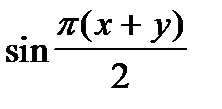Поэтому

V = max [ ; ] =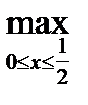

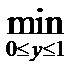
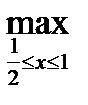
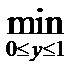
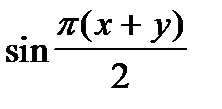= max [ ; ] =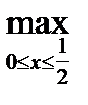

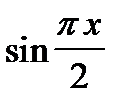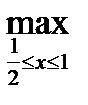
= max [ ; ] = .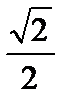

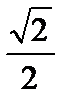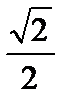При этом значение х получается равным х_o = . Это же значение получается из решения уравнения

= ,

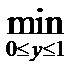
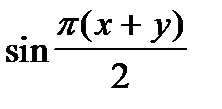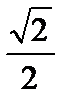т.к. минимум достигается при y = 0, и это уравнение превращается в следующее

= ,

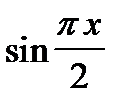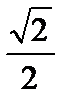откуда следует, что х = .

Заметим, что если в функции выигрышей (5) поменять местами х и y, то она не изменится, а следовательно, эта функция выпукла и по y при всех х Î[0;1]. Поэтому к ней применима та же теория, т.е. у игрока 2 существует оптимальная чистая стратегия y_o, определяемая из уравнения (4)

=

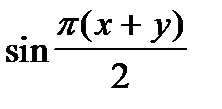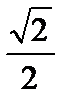
Очевидно, максимум по х достигается при х = , и последнее уравнение примет вид

= .

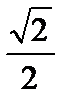Решением последнего уравнения будет y_o = 0. Следовательно, игрок 2 имеет оптимальную чистую стратегию y_o = 0.

Замечание. В приведённом выше примере мы могли определить оптимальную стратегию игрока 1, а игрока 2 - только случайно, в силу “удачного” вида М (х, y).

Рассмотрим теперь метод определения оптимальных стратегий того игрока, для которого функция выигрышей не обязательно выпукла. Пусть непрерывная функция М (х, y), заданная на единичном квадрате, выпукла по y. Нас будет интересовать вопрос нахождения оптимальных стратегий 1 игрока. Предположим также, что для х Î[0; 1], y Î[0; 1] существует частная производная функции М (х, y) по y, причём в точках y = 0 и y = 1 (х, y) = 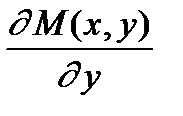понимается как правая и левая производная соответственно. Обозначим через y_o одну из оптимальных чистых стратегий игрока 2 (эта стратегия существует в соответствии с теоремой 4).

Согласно теореме 2 чистые стратегии х игрока 1 могут входить в его оптимальную стратегию с положительной вероятностью, если для них выполняется равенство

М (х, y_o) = V.

Такие чистые стратегии х называются существенными.

Теорема 5. Пусть дана бесконечная антагонистическая игра с непрерывной и дифференцируемой по y на единичном квадрате при любом х функцией выигрышей М (х, y), с оптимальной чистой стратегией y_o игрока 2 и ценой игры V, тогда:

1) если y_o = 1, то среди оптимальных стратегий игрока 1 имеется существенная чистая стратегия х₁, для которой

(х₁, 1) £ 1;

2) если y_o = 0, то среди оптимальных стратегий игрока 1 имеется существенная чистая стратегия х₂, для которой

(х₂, 0) ³ 0;

3) если 0 £ y_o £ 1, то среди оптимальных стратегий игрока 1 найдётся такая, которая является смесью двух существенных стратегий х₁ и х₂. Для этих стратегий

(х₁, y_o) £ 0, (х₂, y_o) ³ 0,

стратегия х₁ употребляется с вероятностью a, стратегия х₂ – с вероятностью (1 - a), где a находится из уравнения

a (х₁, y_o) + (1 - a) (х₂, y_o) = 0.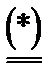

Пример. Пусть функция выигрышей в бесконечной антагонистической игре задана на единичном квадрате и равна

М (х, y) = (х - y)² = х² - 2хy + y².

Эта функция непрерывна по х и y, и поэтому эта игра имеет решение. Кроме того

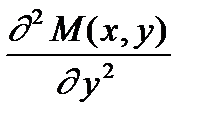= 2 > 0.

Следовательно, М (х, y) выпукла по y, и поэтому согласно теореме 4 цена игры определяется по формуле (1), игрок 2 имеет чистую оптимальную стратегию y_o, определяемую из уравнения (2). Таким образом, имеем

V = 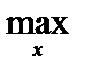(x - y)²;

Для определения 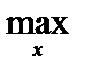(x² - 2xy + y²) последовательно найдём

= 2x - 2 y:= 0 Þ x = y

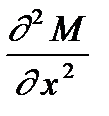= 2 > 0 Þ при x = y функция M имеет минимум для любого y.

Þ максимум достигается в одной из крайних точек x = 0 и (или) x = 1

M (0; y) = y²

M (1; y) = 1 - 2 y + y² = (y - 1)²

Þ V= 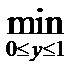max { y²; (1 - y)²}

Данный 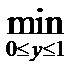max {...} достигается в том случае, если y² = (1 - y)², т.е. y = .

Следовательно V = 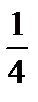при y_o = .

Определим теперь оптимальные стратегии для игрока 1. Поскольку y_o = , то 0 < y_o < 1. Согласно теореме 5 рассмотрим третий случай.

Определим х из уравнения

М (х, y_o) = V,

то есть

(х - )² = .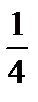

Решая последнее уравнение, получим х₁ = 0, х₂ = 1. Теперь необходимо определить величину a – вероятность применения чистой стратегии х₁ = 0. С этой целью используем уравнение (*).

a (0, ) + (1 - a) (1, ) = 0.

Нетрудно найти

Тогда уравнение для a примет вид:

a - (1 - a) = 0,

откуда a = . Следовательно, стратегия игрока 1

F (х) = J_o (х) + J₁ (х),

а игрока 2

Q (y) = (y).

Здесь через 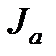(x) обозначена ступенчатая функция

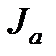(x) = .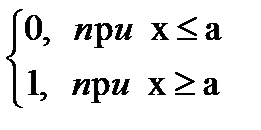

Глава 3. БЕСКОАЛИЦИОННЫЕ ИГРЫ

Антагонистические игры, которые мы изучали ранее, описывают конфликты весьма частного вида. Более того, для большинства имеющих место в реальной жизни конфликтов антагонистические игры либо вовсе не могут считаться приемлемыми, адекватными описаниями, либо, в лучшем случае, могут рассматриваться как первые грубые приближения.

Во-первых, антагонистические игры никак не затрагивают своими описаниями конфликты с числом строк, большим чем два. В месте с тем, такие многосторонние конфликты не только встречаются в действительности, но являются принципиально более сложными, чем конфликты с двумя участниками, и даже не поддаются сведению к последним.

Во-вторых, даже в конфликтах с двумя участниками интересы сторон вовсе не обязаны быть противоположными; во многих конфликтах такого рода случается так, что одна из ситуаций оказывается предпочтительнее другой для обоих участников.

В-третьих, даже если любые две ситуации сравниваются игроками по их предпочтительности противоположным образом, различие разностей в оценках этой предпочтительности оставляет место для соглашений, компромисов и коопераций.

Наконец, в-четвёртых, содержательная острота конфликта не обязательно соответствует его формальной антагонистичности. Например, при встрече двух боевых единиц воюющих сторон (скажем, танков) обоюдное их стремление уничтожить друг друга не выражает антогонистичности конфликта: в антогонистическом конфликте цели сторон оказываются строго противоположными, и стремлению одной стороны уничтожить другую противоположным будет стремление избежать уничтожения.

В качестве примера БАИ рассмотрим:

Дата добавления: 2014-12-16