Табличным способом

Последовательность называется возрастающей (строго), если является возрастающей (строго) числовой функцией, т.е. если .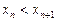

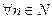Последовательность называется убывающей (строго), если – убывающая (строго) числовая функция, т.е. .

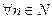Последовательность называется неубывающей, если каждый её член, начиная со второго, не меньше предыдущего, т.е. .

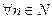Последовательность (х_n) называется невозрастающей, если каждый её член, начиная со второго, не больше предыдущего, т.е. .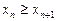

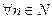Возрастающая и убывающая последовательности называются монотонными последовательностями.

Последовательность называется ограниченной, если существует такие числа m и M, что выполняется неравенство .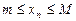

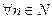Если существует такое число M, что 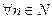, то последовательность называется ограниченной сверху; если существует такое число m, что 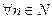, то последовательность называется ограниченной снизу.

Последовательность ограничена тогда и только тогда, когда существует такое положительное число C, что выполняется неравенство

.

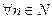Пример 1. Определить, является ли число 28 членом последовательности , если .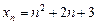

Решение. Число 28 является членом последовательности, если найдётся такой номер 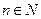, для которого выполняется равенство . Решим это квадратное уравнение 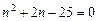, т.е. , . Числа , значит, число 28 не является членом данной последовательности.

Пример 2. Вычислить первые пять членов последовательности 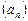, если 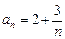. Определить, для каких членов последовательности 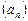выполняется условие .

Решение. Подставляя в формулу общего члена значение n =1,2,3,4,5, получим:

; ;

; ;

.

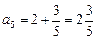Решим неравенство

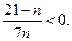
Решением этого неравенства будут . Поэтому для любых членов последовательности с номерами от 1 до 20 включительно выполняется условие .

Пример 3. Последовательность задана следующим образом (реккурентно): и . Вычислить первые 4 ее члена.

Решение: Первый члена последовательности известен: . Для вычисления в заданной формуле для положим . Получим

.

Для вычисления 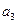в формуле выбираем . Тогда 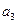выразится через найденный член :

.

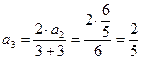Аналогично:

.

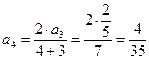Пример 4. Последовательность 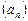задана формулой общего члена: . Задать таблично первые 8 ее членов, изобразить их геометрически и графически.

Решение. Вычислим первые 8 членов заданной последовательности и заполним таблицу.

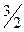
Для геометрической иллюстрации изобразим на числовой оси члены последовательности (рис.1)

Рис.1

В системе координат 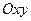укажем точки плоскости, которые имеют координаты для (рис.2).

Рис. 2

Пример 5. Доказать, что последовательность является строго убывающей.

Решение. Если последовательность строго убывающая, то выполняется неравенство 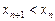или .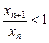

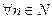Вычисляем

.

Составим отношение

.

Поскольку

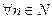, действительно.

Получаем 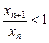для любых натуральных n.

Значит, последовательность является строго убывающей.

Пример 6. Исследовать последователь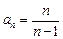ность , на ограниченность.

Решение. Запишем формулу общего члена последовательности следующим образом:

.

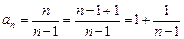Так как 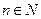и , то , а поэтому

и .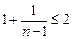

Следовательно, последовательность является ограниченной сверху.

Поскольку неравенство выполняется для всех , то .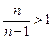

Значит, последовательность является также ограниченной снизу.

Приходим к выводу. что 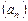– ограниченная последовательность.

Задания для самостоятельного решения

Дата добавления: 2014-12-16