
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Предел функции
|
|
|
|
III уровень
II уровень
I уровень
1.1. Пользуясь определением числовой последовательности, докажите, что:
1) 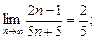 2)
2) 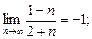
3) 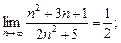 4)
4) 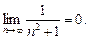
1.2. Вычислите предел:
1) 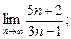 2)
2) 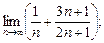
3) 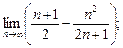 4)
4) 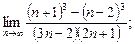
5) 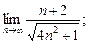 6)
6) 
7) 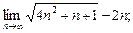 8)
8) 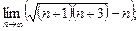
9) 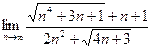 ; 10)
; 10) 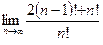 .
.
11) 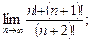 12)
12) 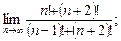
2.1. Вычислите предел:
1) 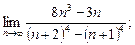 2)
2) 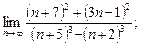
3) 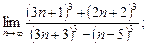 4)
4) 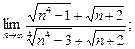
5)  6)
6) 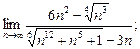
7) 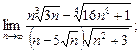 8)
8) 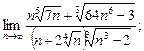
9) 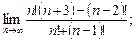 10)
10) 
11) 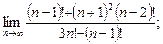 12)
12) 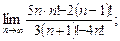
13)  14)
14) 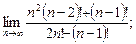
15) 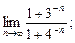 16)
16) 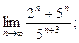
17) 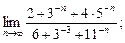 18)
18) 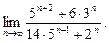
19) 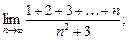 20)
20) 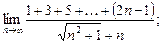
2.2. Докажите, что последовательность 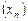 не имеет предела:
не имеет предела:
1) 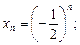 2)
2) 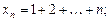
3.1. Задана последовательность
 Найдите
Найдите 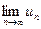 . Определите, каким должно быть
. Определите, каким должно быть 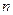 для того, чтобы разность между
для того, чтобы разность между 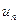 и ее пределом по абсолютной величине не превзошла
и ее пределом по абсолютной величине не превзошла  ?
?
3.2. Вычислите предел последовательности:
1) 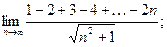 2)
2) 
3) 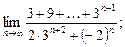 4)
4) 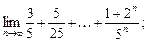
5) 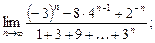 6)
6) 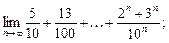
7) 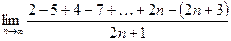 ;
;
8) 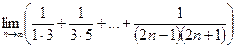 ;
;
9) 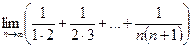 ;
;
10) 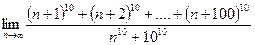 .
.
3.3. Найдите предел последовательности:
1) 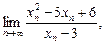 если
если 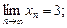
2) 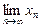 , если
, если 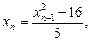
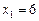 .
.
3.4. Вычислите предел числовой последовательности 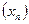 , заданной формулой общего члена при различных значениях параметров
, заданной формулой общего члена при различных значениях параметров 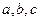 .
.
1)  ;
;
2) 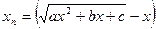 .
.
Рассмотрим функцию  , определённую в некоторой окрестности точки
, определённую в некоторой окрестности точки 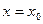 (в самой точке
(в самой точке 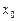 данная функция может быть не определена).
данная функция может быть не определена).
Число А называется пределом функции 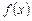 в точке
в точке 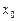 (по Гейне),если для любой последовательности
(по Гейне),если для любой последовательности 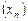 , сходящейся к
, сходящейся к 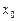
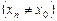 , последовательность
, последовательность 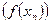 соответствующих значений функции сходится к А.
соответствующих значений функции сходится к А.
Обозначается:
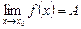
или
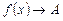 при
при 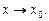
Если функция 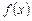 в точке
в точке 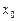 имеет предел, то он единственный.
имеет предел, то он единственный.
Если функции 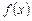 и
и  имеют пределы в точке
имеют пределы в точке 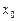 , то справедливы формулы:
, то справедливы формулы:
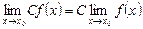 , где С = const; (3)
, где С = const; (3)
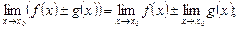 (4)
(4)
 (5)
(5)
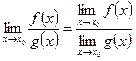 . (6)
. (6)
Если непосредственное вычисление предела по формулам (3) – (6) приводят к неопределённости вида, 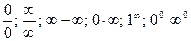 , то необходимо вначале тождественно преобразовать выражение, стоящее под знаком предела.
, то необходимо вначале тождественно преобразовать выражение, стоящее под знаком предела.
Для всех элементарных функций в любой точке их области определения имеет место равенство
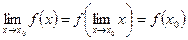 , (7)
, (7)
которое означает, что операции вычисления предела и функции переставимы.
Кроме предела функции в точке рассматривают предел функции на бесконечности: число 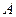 называется пределом функции
называется пределом функции  при
при 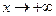 (или
(или 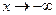 ), если для всякой последовательности
), если для всякой последовательности 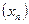 ,
, 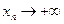 (или
(или 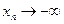 ) при
) при 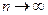 последовательность
последовательность 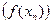 соответствующих значений функции сходится к числу
соответствующих значений функции сходится к числу 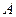 .
.
Обозначают:
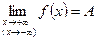 .
.
Для предела функции на бесконечности также справедливы формулы (3) – (6).
Функция 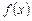 называется бесконечно малой функцией при
называется бесконечно малой функцией при 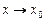 (или
(или 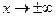 ), если
), если

Функция 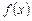 называется бесконечно большой при
называется бесконечно большой при 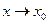
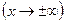 , если для всякой последовательности
, если для всякой последовательности 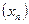 ,
, 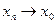 при
при 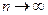 ,
, 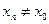 (или
(или 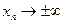 ) последовательность соответствующих значений функции
) последовательность соответствующих значений функции 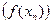 является бесконечно большой.
является бесконечно большой.
Обозначают 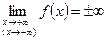 . (8)
. (8)
Если 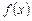 – бесконечно большая функция при
– бесконечно большая функция при 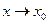
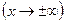 , то она не имеет предела (предел – это число!), запись (8) следует воспринимать лишь как обозначение бесконечно большой функции
, то она не имеет предела (предел – это число!), запись (8) следует воспринимать лишь как обозначение бесконечно большой функции
Пример1. Пользуясь определением предела функции по Гейне доказать, что 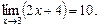
Решение. Пусть 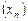 – произвольная последовательность, которая сходится к 3
– произвольная последовательность, которая сходится к 3 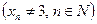 , т.е.
, т.е. 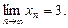
Тогда 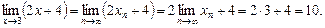
Пример 2. Вычислить пределы функций в точке:
1) 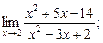 2)
2) 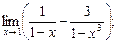
3)  .
.
Решение. 1. При непосредственном использовании формул (3) – (6) получаем неопределённость вида 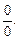
Разложим числитель и знаменатель на множители и сократим дробь на общий множитель. Получим
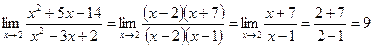 .
.
2. Непосредственное вычисление приводит к неопределённости 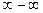 . Для раскрытия приведём выражение в скобках к общему знаменателю:
. Для раскрытия приведём выражение в скобках к общему знаменателю:
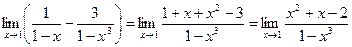 .
.
Далее разлагаем числитель и знаменатель на множители. Получаем
 .
.
3. Непосредственное вычисление предела при 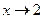 приводит к неопределённости
приводит к неопределённости 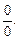 Умножим числитель и знаменатель на неполный квадрат суммы выражений
Умножим числитель и знаменатель на неполный квадрат суммы выражений 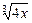 и 2, чтобы в числителе получить разность кубов:
и 2, чтобы в числителе получить разность кубов:
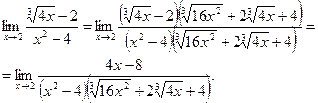
Поскольку неопределенность типа 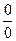 сохранилась, разложим многочлены на множители и сократим:
сохранилась, разложим многочлены на множители и сократим:
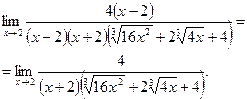
Переход к пределу при 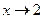 дает
дает
 .
.
Пример 3. С помощью вычислений определить является ли функция  бесконечно малой или бесконечно большой при
бесконечно малой или бесконечно большой при 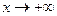 .
.
1)  ; 2)
; 2) 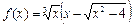
Решение. 1. Чтобы ответить на вопрос задачи, необходимо рассмотреть 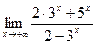 .
.
Непосредственное вычисление этого предела приводит к неопределенности типа 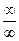 . Вынесем в числителе и знаменателе старшее основание, т.е.
. Вынесем в числителе и знаменателе старшее основание, т.е. 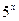 за скобки.
за скобки.
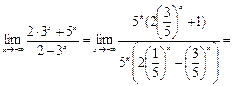

Так как показательная функция 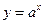 при
при 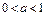 является убывающей, то при
является убывающей, то при 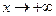 получим:
получим:
 .
.
Тогда согласно определению функция  является бесконечно большой.
является бесконечно большой.
2. Вычислим 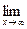
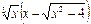 . При
. При  выражение в скобках представляет собой разность двух бесконечно больших величин (
выражение в скобках представляет собой разность двух бесконечно больших величин (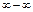 ). Умножив и разделив функцию на выражение
). Умножив и разделив функцию на выражение  , получим:
, получим:
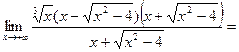
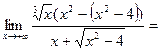
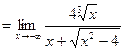 .
.
В результате преобразований возникла неопределенность типа 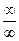 , а поэтому разделим числитель и знаменатель на старшую степень, т.е. на
, а поэтому разделим числитель и знаменатель на старшую степень, т.е. на 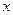 . Получим:
. Получим:
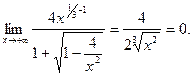
Следовательно, по определению функция 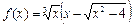 является бесконечно малой.
является бесконечно малой.
Задания для самостоятельного решения
|
|
|
|
|
Дата добавления: 2014-12-16; Просмотров: 460; Нарушение авторских прав?; Мы поможем в написании вашей работы!