
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Адаптивні методи прогнозування
|
|
|
|
Одновимірного ряду динаміки
РОЗДІЛ 7. Економічне прогнозування на основі
Всего 60 баллов.
Методические рекомендации
Колодина
Горбачева
Галина Павловна
Наталья Федоровна
СТАТИСТИКА
Методические рекомендации выходят в авторской редакции
Подп. в пеать 00.00.00. Формат 60x80 1/16.
Бум. офсетная. Гарнитура «Times». Печать цифровая. Объем 00 усл. печ. л. Тираж 000 экз. Заказ № 00.
Оренбургский государственный институт менеджмента
460038, г. Оренбург, ул. Волгоградская, д. 16.
Тел./факс: (3532) 36-19-62, 36-48-18
Отпечатано в типографии ГОУВПО «ОГИМ»
460038, г. Оренбург, ул. Волгоградская, д. 16.
Методи кореляційно-регресійного аналізу, за допомогою яких здійснюють аналітичне вирівнювання рядів динаміки, слугують важливим інструментом передбачення значень майбутніх рівнів. Однак прогнози, які складені на основі моделей аналітичного вирівнювання, можна вважати надійними, за виконання, принаймні таких вимог:
• обсяг вибірки, який використаний для побудови рівняння регресії, є достатньо великим;
• виконуються основні припущення регресійного аналізу;
• коефіцієнти рівняння регресії, яке описує тренд, залишаються незмінними протягом досліджуваного періоду.
Якщо ж вказані вимоги не виконуються, то застосування регресійних моделей для обчислення прогнозних значень рядів динаміки може призвести до хибних результатів.
Ефективними методами прогнозування на основі одновимірних рядів динаміки вважаються адаптивні методи. Вони забезпечують побудову моделей, які самокоригуються на підставі результату прогнозу, зробленого на попередньому кроці, і різної інформаційної цінності рівнів ряду динаміки. Одним із методів, які забезпечують оперативне реагування на умови, що змінюються, є метод експоненційного згладжування Р.Брауна.
За методом Брауна при прогнозуванні враховують всі рівні динамічного ряду, але вважають, що початкові рівні дають менш вагому інформацію, ніж кінцеві. Динамічний ряд вирівнюють за допомогою зваженої плинної середньої, яка визначає значення члена ряду в кінці інтервалу вирівнювання, причому ваги підпорядковуються експоненційному закону. Допускаючи, що досліджуване явище в прогнозованому періоді буде розвиватися так само, як і в аналізованому, можна вважати зважену плинну середню з експоненційно розподіленими вагами ефективним засобом прогнозування.
Розрахунок прогнозних значень будується на використанні експоненційних середніх, які слугують для обчислення рекурентних поправок до коефіцієнтів полінома, що описує тренд динамічного ряду. Експоненційною середньою першого порядку динамічного ряду для моменту t називають таку величину:
 , (7.1)
, (7.1)
де α – параметр згладжування (0< α<1).
Експоненційні середні вищих порядків обчислюють за такою рекурентною формулою:
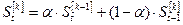 . (7.2)
. (7.2)
Як видно із (7.2), експоненційна середня 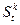 - це лінійна комбінація попередніх спостережень із вагами, які зменшуються згідно з геометричною прогресією стосовно минулих рівнів.
- це лінійна комбінація попередніх спостережень із вагами, які зменшуються згідно з геометричною прогресією стосовно минулих рівнів.
На підставі (7.2) рекурентні співвідношення для знаходження експоненційних середніх можна представити у вигляді:
 (7.3)
(7.3)
Якщо допустити, що ряд динаміки описується поліномом р-го порядку
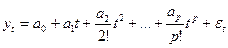 , (7.4)
, (7.4)
то прогнозне значення в момент 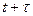 може бути знайдене з допомогою розкладу в ряд Тейлора:
може бути знайдене з допомогою розкладу в ряд Тейлора:
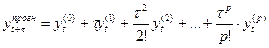
 , (7.5)
, (7.5)
де 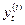 - і-та похідна в момент часу t.
- і-та похідна в момент часу t.
Брауном і Маєром доведено, що будь-яку і-т похідну рівняння (7.5) можна обчислити як лінійну комбінацію експоненційних середніх до (р+1)-го порядку. Мета експоненційного згладжування – розрахунок рекурентних уточнень коефіцієнтів в (7.4).
Першим етапом процедури експоненційного згладжування є розрахунок тренду ряду динаміки. На практиці найчастіше користуються лінійною або квадратичною моделями:
 ; (7.6)
; (7.6)
 . (7.7)
. (7.7)
З урахуванням вибраної моделі тренду прогноз на період 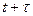 знаходять за формулами:
знаходять за формулами:
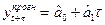 ; (7.8)
; (7.8)
 , (7.9)
, (7.9)
де 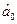 і
і 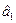 та
та 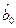 ,
,  і
і  - оцінювальні коефіцієнти, що зв’язують експоненційні середні відповідно з коефіцієнтами рівняння тренду (7.6) та (7.7).
- оцінювальні коефіцієнти, що зв’язують експоненційні середні відповідно з коефіцієнтами рівняння тренду (7.6) та (7.7).
Другим етапом процедури експоненційного згладжування є визначення початкових умов прогнозування – вибір коефіцієнта згладжування α і обчислення значень  .
.
Чітких рекомендацій щодо знаходження оптимального значення коефіцієнта згладжування α нема. Але треба враховувати те, що чим більше значення α, тим істотнішим для розрахунку прогнозних значень буде вплив останніх спостережень. Найчастіше значення α вибирають з урахуванням довжини інтервалу згладжування за такою формулою:
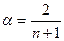 , (7.10)
, (7.10)
де n – кількість спостережень, що входять в інтервал згладжування.
Значення коефіцієнта згладжування можна підібрати в процесі моделювання, із урахуванням відхилень фактичних рівнів ряду динаміки від розрахованих за прогнозною формулою.
Для лінійного тренду початкові значення експоненційних середніх можна вибрати користуючись значеннями коефіцієнтів рівняння регресії (7.6):
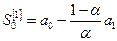 ; (7.11)
; (7.11)
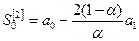 . (7.12)
. (7.12)
Початкові значення експоненційних середніх для квадратичної моделі тренду обчислюють за такими формулами:

 ; (7.13)
; (7.13)
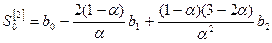 ; (7.14)
; (7.14)
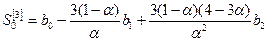 . (7.15)
. (7.15)
Наступним етапом прогнозування є рекурентне обчислення експоненційних середніх і оцінювальних коефіцієнтів.
Якщо тренд описується лінійною моделлю, то оцінювальні коефіцієнти розраховують за формулами:
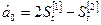 ; (7.16)
; (7.16)
 . (7.17)
. (7.17)
У разі квадратичної моделі тренду оцінювальні коефіцієнти дорівнюють:
 ; (7.18)
; (7.18)
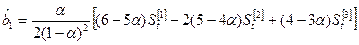 ; (7.19)
; (7.19)
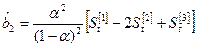 . (7.20)
. (7.20)
На підставі розрахованих оцінювальних коефіцієнтів згідно з (7.8) і (7.9) обчислюють прогнозні значення. Середнє квадратичне відхилення похибки прогнозу для лінійної моделі тренду визначають за формулою:
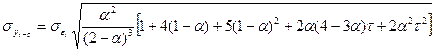 , (7.21)
, (7.21)
а для квадратичної – за такою формулою
 , (7.22)
, (7.22)
де 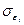 - середня квадратична похибка відхилення фактичних даних від прогнозних.
- середня квадратична похибка відхилення фактичних даних від прогнозних.
Середня квадратична похибка відхилення фактичних даних від прогнозних для лінійної моделі буде становити:
 , (7.23)
, (7.23)
а для квадратичної моделі –
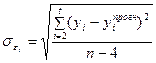 . (7.24)
. (7.24)
Вважаючи, що випадкова величина 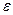 є нормально розподіленою з нульовим математичним сподіванням і дисперсією
є нормально розподіленою з нульовим математичним сподіванням і дисперсією  , можна визначити довірчий інтервал прогнозного значення для вибраного рівня істотності α:
, можна визначити довірчий інтервал прогнозного значення для вибраного рівня істотності α:
 . (7.25)
. (7.25)
Приклад 7.1. Обсяг продукції, реалізованої фірмою за 16 років, характеризується даними, наведеними у табл.7.1.
Таблиця 7.1
| Рік | Обсяг випуску, тис.грн. | Рік | Обсяг випуску, тис.грн. |
| t =1 | t =9 | ||
| t =2 | t =10 | ||
| t =3 | t =11 | ||
| t =4 | t =12 | ||
| t =5 | t =13 | ||
| t =6 | t =14 | ||
| t =7 | t =15 | ||
| t =8 | t =16 |
За даними табл.7.1 необхідно розрахувати прогнозне значення обсягу реалізації продукції у t=17 році, користуючись методом експоненційного згладжування.
Дослідження тренду, який описує залежність між обсягом реалізованої продукції і часом, з допомогою лінійної і квадратичної моделей показало, що кращою моделлю є квадратичне рівняння регресії:
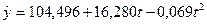 .
.
З урахуванням числових значень параметрів нелінійного тренду і емпірично встановленого значення коефіцієнта згладжування α=2/17=0,118 знаходимо початкові умови згідно з (7.13) – (7.15):
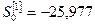 ,
,
 ,
,
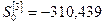 .
.
Користуючись наведеними вище формулами для розрахунку експоненційних середніх, оцінювальних коефіцієнтів та розрахунку прогнозів, знаходимо їхнє значення для кожного року динамічного ряду (табл.7.2).
Точковий прогноз на t=17 рік становить:
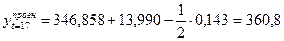 (тис.грн.)
(тис.грн.)
У результаті дослідження тренду динамічного ряду було встановлено, що середньоквадратичне відхилення дорівнює 4,058. Тоді середнє квадратичне відхилення похибки прогнозу буде становити 2,15.
Знаходимо межі індивідуального прогнозного значення для рівня значущості α=0,05:
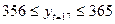 (тис.грн.).
(тис.грн.).
Отже, з ймовірністю р=0,95 стверджуємо, що обсяг випуску продукції t=17 році буде не меншим за 356 тис.грн. і не більшим за 365 тис.грн.
Основними умовами ефективної реалізації методу Р.Брауна слід вважати:
• відносну інерційність у розвитку прогнозованого процесу, яка полягає у тому, що істотні зміни характеристик процесу можливі за певний достатньо значний період;
• відсутність стрибків (стрибкоподібних тенденцій) у рівнях ряду динаміки;
• період часу, для якого існує інформаційна база прогнозування, повинен бути достатнім для встановлення основних закономірностей розвитку прогнозованого процесу;
• оптимальність вибору значення параметра згладжування, який визначає ваговий вплив різних рівнів ряду динаміки на прогнозований показник.
Таблиця 7.2
| Рік | 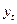
| 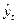
| 
| 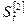
| 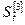
| 
| 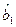
| 
| 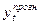
|
| t=1 | 120,7083 | -8,45011 | -145,955 | -291,088 | 121,4257 | 16,23179 | -0,13562 | ||
| t=2 | 136,7809 | 8,896966 | -127,737 | -271,871 | 138,0312 | 16,15128 | -0,13333 | 137,5897 | |
| t=3 | 152,7141 | 25,37968 | -109,723 | -252,794 | 152,5143 | 15,81802 | -0,14166 | 154,1158 | |
| t=4 | 168,5079 | 41,92324 | -91,8825 | -233,864 | 167,5536 | 15,58798 | -0,14534 | 168,2615 | |
| t=5 | 184,1624 | 58,87345 | -74,1465 | -215,073 | 183,9864 | 15,55719 | -0,14057 | 183,0689 | |
| t=6 | 199,6775 | 75,47657 | -56,5438 | -196,423 | 199,6382 | 15,43721 | -0,13971 | 199,4734 | |
| t=7 | 215,0533 | 92,00874 | -39,067 | -177,91 | 215,3169 | 15,33636 | -0,13809 | 215,0056 | |
| t=8 | 230,2897 | 107,7724 | -21,7918 | -159,543 | 229,1491 | 15,01912 | -0,14556 | 230,5842 | |
| t=9 | 245,3868 | 123,4463 | -4,70495 | -141,327 | 243,1264 | 14,75259 | -0,1506 | 244,0955 | |
| t=10 | 260,3445 | 139,629 | 12,27552 | -123,256 | 258,8043 | 14,72691 | -0,14539 | 257,8037 | |
| t=11 | 275,1628 | 155,908 | 29,17346 | -105,323 | 274,8802 | 14,759 | -0,138 | 273,4585 | |
| t=12 | 289,8418 | 172,0365 | 45,98087 | -87,5229 | 290,6439 | 14,75504 | -0,13241 | 289,5702 | |
| t=13 | 304,3814 | 188,3851 | 62,73431 | -69,8455 | 307,1069 | 14,8441 | -0,12318 | 305,3327 | |
| t=14 | 318,7817 | 203,5163 | 79,29689 | -52,2994 | 320,3588 | 14,52984 | -0,13114 | 321,8894 | |
| t=15 | 333,0426 | 218,632 | 95,68926 | -34,8889 | 333,9393 | 14,28837 | -0,13574 | 334,823 | |
| t=16 | 347,1642 | 233,3812 | 111,8883 | -17,621 | 346,8576 | 13,99007 | -0,14252 | 348,1598 |
Іншим методом адаптивного прогнозування, який грунтується на принципі різної інформаційної цінності окремих рівнів ряду динаміки для розрахунку прогнозованого показника, є метод гармонійних ваг, розроблений З.Хелдвігом. В основу цього методу, як і методу експоненційного згладжування Р.Брауна, покладена ідея зважування плинного показника, але замість плинної середньої застосовується плинний тренд. Окремі точки плинного тренду (ламаної лінії) зважуються за допомогою гармонійних ваг, що забезпечує присвоєння пізнішим спостереженням вищої вагомості.
Першим кроком реалізації методу гармонійних ваг є формування фаз. До фази входять k рівнів початкового ряду динаміки у1, у2,,...,уn (з практичного погляду рекомендують вибирати k таким, що дорівнює від 3 до 5). Першу фазу утворюють рівні у1, у2,,...,уk, другу – у2, у3,,...,уk+1, останню – уn-k+1, уn-k+2,,...,уn. Очевидно, що кількість утворених фаз буде дорівнювати K=n-k+1.
Після того, як сформовані фази, для кожної з них за допомогою методу найменших квадратів знаходимо параметри лінійних трендів:
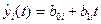
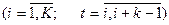 . (7.26)
. (7.26)
На основі (7.26) обчислюють середні значення плинного тренду в точках 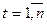 . Наприклад, якщо k=3, то для знаходження середніх значень використовуємо співвідношення:
. Наприклад, якщо k=3, то для знаходження середніх значень використовуємо співвідношення:
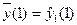 ;
;
 ;
;
 ; (7.27)
; (7.27)
 ;
;
.............;
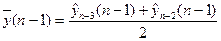 ;
;
 .
.
Для виконання наступних кроків необхідно перевірити припущення про те, що відхилення від плинного тренду мають випадковий характер і становлять стаціонарний процес. Для цього використовують автокореляційну функцію помилок.
Якщо відзначене припущення виконується, то наступним кроком реалізації методу гармонійних ваг є розрахунок середніх приростів. Спочатку розраховують прирости за такою формулою:
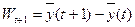 , (7.28)
, (7.28)
а потім знаходять середній приріст за формулою:
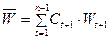 . (7.29)
. (7.29)
Величини 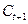 - гармонійні коефіцієнти, які розраховують на підставі гармонійних ваг. Для визначення гармонійних ваг користуються співвідношенням:
- гармонійні коефіцієнти, які розраховують на підставі гармонійних ваг. Для визначення гармонійних ваг користуються співвідношенням:
 , (7.30)
, (7.30)
або

 (7.31)
(7.31)
Найбільш ранній інформації надається вага 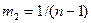 .
.
На підставі (7.31) отримуємо:
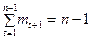 . (7.32)
. (7.32)
Гармонійні коефіцієнти визначаємо за формулою:
 . (7.33)
. (7.33)
Очевидно, що гармонійні коефіцієнти відповідають таким умовам:
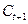 > 0
> 0  ; (7.34)
; (7.34)
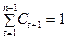 . (7.35)
. (7.35)
За описаною вище схемою розрахунку гармонійних коефіцієнтів кожна наступна інформація має вищу вагомість, ніж попередня.
Точковий прогноз знаходять як суму останнього значення ряду динаміки і середнього приросту:
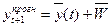 . (7.36)
. (7.36)
Довірчий інтервал прогнозного значення знаходять, користуючись нерівністю Чебишева для випадкової величини 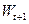 :
:
 >
>  <
< 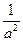 , (7.37)
, (7.37)
де а – задане ціле додатнє число;
 - середнє квадратичне відхилення випадкової величини, оцінка якого становить:
- середнє квадратичне відхилення випадкової величини, оцінка якого становить:
 . (7.38)
. (7.38)
Довірчі границі для прогнозного значення показника будуть становити:
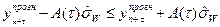 , (7.39)
, (7.39)
де  - горизонт прогнозування, а величину
- горизонт прогнозування, а величину  розраховують за формулою (7.40):
розраховують за формулою (7.40):
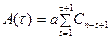 . (7.40)
. (7.40)
Приклад 7.2. За рядом динаміки, наведеним у попередньому прикладі, скласти прогноз обсягу випуску продукції на t=17 рік, користуючись методом гармонійних ваг.
Аналіз початкового ряду динаміки свідчить про відсутність різких стрибків, а інформаційна база є достатньою для прогнозування, що є підставою правомірності застосування методу гармонійних ваг.
Кількість членів ряду динаміки, які утворюють фазу, встановимо такою, що дорівнює k=5. Для кожної фази, застосовуючи метод найменших квадратів, будуємо рівняння плинних трендів (табл.7.3):
На підставі побудованих рівнянь регресії знаходимо значення плинного тренду:
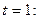
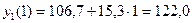 ;
;
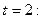
 ,
,
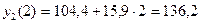 ;
;
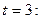
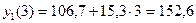 ,
,
 ,
,
 ;
;
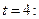
 ,
,
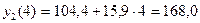 ,
,
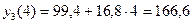 ,
,
 ;
;
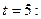
 ,
,
 ,
,
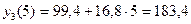 ,
,
 ,
,
 ;
;
................

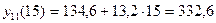 ,
,
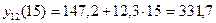 ;
;

 .
.
Далі розраховуємо середні значення плинного тренду у точках 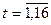 :
:
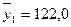 ;
;
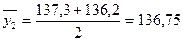 ;
;
 ;
;
...............
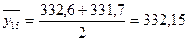 ;
;
 .
.
Таблиця 7.3
Рівняння плинних трендів
| Фази динамічного ряду (к=5) | Порядковий номер періоду | |||||||||||||||

| 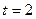
| 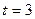
| 
| 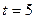
| 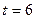
| 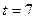
| 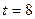
| 
| 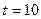
| 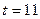
| 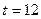
| 
| 
| 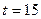
| 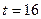
| |
| Фаза 1 | 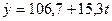 
| |||||||||||||||
| Фаза 2 | 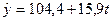 
| |||||||||||||||
| Фаза 3 |  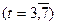
| |||||||||||||||
| Фаза 4 |  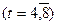
| |||||||||||||||
| Фаза 5 | 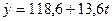 
| |||||||||||||||
| Фаза 6 | 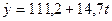 
| |||||||||||||||
| Фаза 7 | 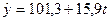 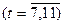
| |||||||||||||||
| Фаза 8 | 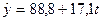 
| |||||||||||||||
| Фаза 9 |  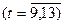
| |||||||||||||||
| Фаза 10 | 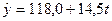 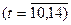
| |||||||||||||||
| Фаза 11 |  
| |||||||||||||||
| Фаза 12 |  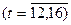
|
У результаті отримаємо такий ряд динаміки середніх величин:
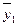
| 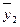
| 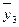
| 
| 
| 
| 
| 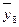
|
| 122,0 | 136,75 | 151,5 | 167,825 | 184,18 | 199,68 | 214,26 | 227,82 |
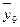
| 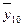
| 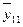
| 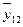
| 
| 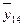
| 
| 
|
| 242,8 | 260,18 | 278,58 | 293,56 | 307,75 | 319,933 | 332,15 |
Для перевірки гіпотези про те, що відхилення від плинного тренду утворюють стаціонарний процес, будуємо автокореляційну функцію. Значення автокореляційної функції спадають, тобто гіпотеза про те, що помилки мають випадковий характер і відображають стаціонарний процес, підтверджується.
Розраховуємо прирости:
| W2 | W3 | W4 | W5 | W6 | W7 | W8 | W9 |
| 14,75 | 14,75 | 16,325 | 16,355 | 15,5 | 14,58 | 13,56 | 14,98 |
| W10 | W11 | W12 | W13 | W14 | W15 | W16 | |
| 17,38 | 18,4 | 14,98 | 14,19 | 12,183 | 12,217 | 11,85 |
Користуючись співвідношеннями (7.31) і (7.36), обчислюємо гармонійні ваги mt і гармонійні коефіцієнти 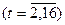 :
:
| m2 | m3 | m4 | m5 | m6 | m7 | m8 | m9 |
| 0,067 | 0,138 | 0,215 | 0,298 | 0,389 | 0,489 | 0,600 | 0,725 |
| m10 | m11 | m12 | m13 | m14 | m15 | m16 | |
| 0,868 | 1,035 | 1,235 | 1,485 | 1,818 | 2,318 | 3,318 | |
| C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 |
| 0,004 | 0,009 | 0,014 | 0,020 | 0,026 | 0,033 | 0,040 | 0,048 |
| C10 | C11 | C12 | C13 | C14 | C15 | C16 | |
| 0,057 | 0,069 | 0,082 | 0,099 | 0,121 | 0,156 | 0,221 |
Знайдені значення гармонійних коефіцієнтів з практичного погляду відповідають умовам (7.34) і (7.35).
За формулою (7.29) знаходимо середній приріст:
 .
.
З урахуванням цього точковий прогноз на t=17 рік згідно (7.36) становитиме:
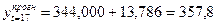 (тис.грн.).
(тис.грн.).
На підставі (7.38), оцінка середнього квадратичного відхилення випадкової величини W буде становити:
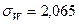 .
.
Приймемо α=4 і з (7.40) та (7.39) послідовно отримаємо:
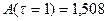 ;
;
 (тис.грн.).
(тис.грн.).
Отже, з ймовірністю р=0,954 стверджуємо, що інтервальний прогноз буде в межах від 355 до 360 тис.грн.
Порівнюючи результати прогнозування, які отримано з допомогою методу експоненційного згладжування і за допомогою методу гармонійних ваг, можна зробити висновок про те, що в такому разі з практичного погляду вони збігаються.
|
|
|
|
|
Дата добавления: 2014-12-16; Просмотров: 3221; Нарушение авторских прав?; Мы поможем в написании вашей работы!