Прогнозування сезонних явищ

Для прогнозування рядів, у яких варіація рівнів має сезонний характер, використовують моделі з виділеним трендом і сезонною компонентою. Найпоширенішими моделями такого типу вважаються моделі з адитивною і мультиплікативною компонентами.

У моделі із адитивною компонентою значення членів ряду динаміки подають за допомогою суми трендового значення (Т), сезонної варіації (S) і похибки (Е):

. (7.41)

У моделі з мультиплікативною компонентою значення членів ряду динаміки подають як добуток величин T, S, E:

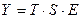. (7.42)

На відміну від моделі з адитивною компонентою, в якій сезонні компоненти є сталими величинами, у мультиплікативних моделях сезонні значення збільшуються або зменшуються зі зміною трендових значень, тобто становлять певну частину даного трендового значення.

Загальна процедура моделювання полягає у виконанні таких кроків:

• обчислення значень сезонної компоненти;

• елімінування сезонної компоненти (десезоналізація даних);

• розрахунок тренду;

• розрахунок прогнозних значень;

• розрахунок похибок прогнозу.

Знаходження оцінок сезонної компоненти здійснюють з використанням середньої плинної. У деяких випадках (наприклад, при вирівнюванні ряду динаміки за чотирма точками під час прогнозування на підставі квартальних даних) оцінки є точками, що лежать між фактичними значеннями рівнів динамічного ряду, хоча повинні відповідати фактичним. Для цього знаходять центровані середні плинні – середні із пари сусідніх значень.

На підставі знайдених значень сезонних компонент розраховують середні сезонні оцінки. Середні оцінки переважно коригують так, щоб їхня сума дорівнювала нулю для адитивної моделі і чотирьом – для мультиплікативної моделі. У першому випадку кожну середню оцінку збільшують (зменшують) на константу, а у другому – множать (ділять) на константу.

Розглянемо модель з адитивною компонентою.

Віднявши значення сезонних компонент від фактичних значень ряду динаміки отримаємо:

. (7.43)

Знайдені десезоналізовані значення (Т+Е) використовують для побудови моделі основного тренду за допомогою рівняння регресії:

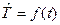, (7.44)

де t – порядковий номер періоду.

Прогнозне значення динамічного ряду обчислюють за формулою:

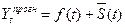, (7.45)

де S(t) – середнє значення сезонної компоненти для періоду t.

Мірою відповідності прогнозованих значень фактичним даним можуть слугувати середнє абсолютне відхилення або середня похибка, які обчислюють відповідно за формулами:

, (7.46)

. (7.47)

Приклад 7.3. Динаміка обсягу виробництва твердих сирів на підприємстві молочно-харчової промисловості характеризується даними, наведеними у табл.7.4. Скласти прогноз обсягу випуску продукції на 1-4-ий квартали t=13 року з допомогою моделі з адитивною компонентою.

Таблиця 7.4

Інтервал часу, рік, квартал	Обсяг виробництва продукції, тис.грн.	Інтервал часу, рік, квартал	Обсяг виробництва продукції, тис.грн.
Разом		Разом
Разом		Разом
Разом		Разом
Разом		Разом
Разом		Разом
Разом		Разом

Візуальний аналіз табл.7.4 і рис.7.1 свідчить про те, що в динаміці обсягів випуску твердих сирів спостерігається регулярна сезонна тенденція зміни ряду динаміки. Сумарні річні обсяги випуску продукції мають чітко виражену тенденцію до зростання, проте у четвер­тому кварталі відбувається спад порівняно із третім. Причиною таких зако­номірностей зміни обсягів випуску твердих сирів можна вважати характер зміни сиро­винної бази – виробництва молока у регіоні.

t, квартал

Рис.7.1. Динаміка обсягу виробництва твердих сирів

Для урахування впливу сезонності під час побудови квартальних прогнозів користуються методами сезонної декомпо­зиції, зокрема моделлю з адитивною компонентою.

Для виявлення тренду динамічного ряду, на рівні якого впливає сезонність, застосуємо метод середніх плинних і найменших квадратів. Плинна середня, яка використовується для цього, має строго визначений період – чо­тири квартали. Для віднесення середньої плинної до певного місяця потрібно здійснити центрування.

Як наслідок отримаємо середні, які можна вважати вільними від сезонних коливань. Віднявши від фактичних значень рівнів динамічного ряду значення центрованих середніх плинних, одержимо оцінки сезонних компонент S адитивної моделі. Розрахунок сезонних оцінок подано в табл.7.5.

На підставі знайдених оцінок сезонних компонент обчислюємо відкориговані середні значення сезонних компонент для кожного кварталу (їх сума дорівнює 0):

;

;

;

.

Значення сезонних компонент віднімаємо від фактичних рівнів динамічного ряду і отримуємо десезоналізовані значення обсягів випуску продукції (табл.7.6), які слугують даними для побудови рівняння тренду. Як рівняння тренду вибираємо лінійну функцію. Скориставшись стандартною функцією ЛИНЕЙН в системі EXCEL, одержимо такі результати:

• рівняння регресії: 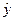= 399,731 + 7,596t;

• розрахункове значення F-критерію: F_розр = 1508,45;

• розрахункові значення t-критерію: ; .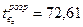

Порівнюючи розрахункові значення критеріїв з табличними для ймовірності р = 0,95, робимо висновок про адекватність регресійної моделі тренду і статистичну значущість коефіцієнтів рівняння регресії.

На підставі знайденого лінійного рівняння тренду будуємо адитивну модель прогнозування:

.

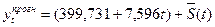Прогнозні значення, отримані за цією моделлю, і відхилення фактичних значень від прогнозних представлені в табл.7.6.

Таблиця 7.5

Розрахунок оцінок сезонних компонент для адитивної моделі

Інтервал часу, рік, квартал	Обсяг виробництва продукції, тис.грн.	Разом за 4 квартали	Середня плинна за 4 квартали	Центрована середня плинна	Оцінка сезонної компоненти
			392,5
				398,75	31,25
				416,25	-56,25
				427,5
					438,75	-18,75
				456,25	43,75
			462,5
			467,5
				468,75	-58,75
					471,25	-31,25
			472,5
				473,75	36,25
				487,5	-67,5
					492,5	-12,5
				497,5	32,5
				503,75	46,25
			507,5
				516,25	-76,25
					533,75	-23,75
			542,5
			547,5
				553,75	66,25
				562,5	-102,5
					567,5	-7,5
				581,25	38,75
			592,5

Продовження табл. 7.5

				597,5
				601,25	-51,25
						-30
				613,75	36,25
			612,5
			617,5
				621,25	-81,25
					628,75	-28,75
			632,5
				637,5	42,5
			642,5
			647,5
				648,75	-68,75
					653,75	-33,75
			657,5
			662,5
			667,5
				672,5	-72,5
				677,5
					681,25	-41,25
				687,5	42,5
				692,5	77,5
				698,75	-78,75
				702,5
						-45
			707,5
			712,5
			717,5
				722,5	-82,5
				727,5
					731,25	-51,25
				737,5	62,5

Таблиця 7.6

Десезоналізовані і прогнозні обсяги випуску продукції, які розраховані за допомогою адитивної моделі

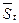
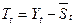
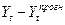
Інтервал часу, рік, квартал	Обсяг випуще­ної про­дукції, тис.грн. ,Yt	Значення сезонної компо­ненти,	Десезоналі-зований випуск,	Номер періоду, t	Прог- ноз,	Абсолютна похибка прогнозу,	Відносна похибка прогнозу,
			-29,4602	399,4602		377,8672	-7,86719	0,021263
		42,69886	367,3011		457,6223	-47,6223	0,116152
		59,17614	370,8239		481,6955	-51,6955	0,120222
		-72,4148	432,4148		357,7006	2,299364	0,006387
			-29,4602	449,4602		408,2512	11,74882	0,027973
		42,69886	457,3011		488,0063	11,99374	0,023987
		59,17614	460,8239		512,0795	7,920466	0,015232
		-72,4148	482,4148		388,0846	21,91538	0,053452
			-29,4602	469,4602		438,6352	1,364837	0,003102
		42,69886	467,3011		518,3903	-8,39025	0,016451
		59,17614	470,8239		542,4635	-12,4635	0,023516
		-72,4148	492,4148		418,4686	1,531394	0,003646
			-29,4602	509,4602		469,0191	10,98085	0,022877
		42,69886	487,3011		548,7742	-18,7742	0,035423
		59,17614	490,8239		572,8475	-22,8475	0,041541
		-72,4148	512,4148		448,8526	-8,85259	0,02012
			-29,4602	539,4602		499,4031	10,59687	0,020778
		42,69886	557,3011		579,1582	20,84178	0,034736
		59,17614	560,8239		603,2315	16,76851	0,027046
		-72,4148	532,4148		479,2366	-19,2366	0,041819
			-29,4602	589,4602		529,7871	30,21288	0,053952
		42,69886	577,3011		609,5422	10,45779	0,016867
		59,17614	580,8239		633,6155	6,384525	0,009976
		-72,4148	622,4148		509,6206	40,37944	0,073417
			-29,4602	609,4602		560,1711	19,8289	0,034188
		42,69886	607,3011		639,9262	10,07381	0,015498
		59,17614	620,8239		663,9995	16,00054	0,02353
		-72,4148	612,4148		540,0045	-0,00455	8,42E-06
			-29,4602	629,4602		590,5551	9,44491	0,015742
		42,69886	637,3011		670,3102	9,689823	0,01425
		59,17614	650,8239		694,3834	15,61655	0,021995
		-72,4148	652,4148		570,3885	9,611467	0,016571
			-29,4602	649,4602		620,9391	-0,93907	0,001515
		42,69886	647,3011		700,6942	-10,6942	0,015499
		59,17614	680,8239		724,7674	15,23257	0,020585
		-72,4148	672,4148		600,7725	-0,77252	0,001288
			-29,4602	669,4602		651,3231	-11,3231	0,017692
		42,69886	687,3011		731,0781	-1,07815	0,001477
		59,17614	710,8239		755,1514	14,84858	0,019284
		-72,4148	692,4148		631,1565	-11,1565	0,017994

Продовження табл.7.6

			-29,4602	689,4602		681,707	-21,707	0,032889
		42,69886	717,3011		761,4621	-1,46213	0,001924
		59,17614	730,8239		785,5354	4,464598	0,005651
		-72,4148	712,4148		661,5405	-21,5405	0,033657
			-29,4602	709,4602		712,091	-32,091	0,047193
		42,69886	757,3011		791,8461	8,153882	0,010192
		59,17614	760,8239		815,9194	4,080613	0,004976
		-72,4148	732,4148		691,9245	-31,9245	0,04837
			-29,4602			742,475
		42,69886			822,2301
		59,17614			846,3034
		-72,4148			722,3085

Згідно з результатами моделювання з допомогою адитивної моделі прогнозні значення квартальних випусків твердих сирів становлять:

= 743 (тис.грн.);

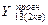= 822 (тис.грн.);

= 846 (тис.грн.);

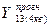= 722 (тис.грн.).

Середня відносна похибка прогнозування за ретроспективними даними становить 2,61%, що можна вважати досить високим показником якості прогнозу.

Прогнозування на основі моделі з мультиплікативною компонентою здійснюють аналогічно. Відмінність полягає лише в обчисленні оцінки сезонної компоненти.

Оцінка сезонної компоненти для мультиплікативної моделі дорівнює частці від ділення фактичного значення рівня ряду динаміки на значення центрованої середньої плинної. На підставі оцінок сезонних компонент знаходять їхнє середнє значення, після чого середні значення коригуються (сума повинна дорівнювати 4).

На підставі відкоригованих середніх значень сезонних оцінок знаходять десезоналізовані ріні ряду динаміки:

(7.48)

Прогнозні значення для моделі з мультиплікативною компонентою обчислюють за формулою:

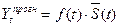, (7.49)

де f(t) і S(t) мають таку ж інтерпретацію, як і в (7.45).

Приклад 7.4. Користуючись даними табл.7.4, скласти прогноз обсягу випуску продукції на І-ІV квартали t=13 року за допомогою мультиплікативної моделі.

За значеннями центрованих середніх плинних (табл.7.5) знаходимо оцінки сезонних компонент та їхні відкориговані середні значення.

В табл.7.7 наведено результати обчислення оцінок сезонних компонент для мультиплікативної моделі. Відкориговані (сума дорівнює 4) середні значення сезонних компонент для кожного кварталу відповідно становлять:

;

;

;

.

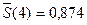Поділивши фактичні значення рівнів динамічного ряду на середні значення сезонних компонент, отримаємо десезоналізовані рівні (табл.7.7), на основі яких будуємо рівняння тренду:

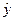= 399,637 + 7,61t.

Розрахункові значення F-критерію та t-критеріїв становлять:

F_розр = 1927,83;

;

.

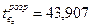Таблиця 7.7

Десезоналізовані і прогнозні обсяги випуску, які обчислені за допомогою мультиплікативної моделі

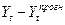
Інтер-вал ча-су, рік, квартал	Обсяг виробни-цтва про-дукції, Yt, тис.грн.	Оцінка сезонної компо-ненти	Відкориго-ване середнє значення сезонної компоненти, St	Десезона­лізований випуск, Tt=Yt/St	Но- мер періо-ду, t	Прогноз, тис.грн.,	Абсолют-на похиб-ка прогно-зу,	Відносна похибка прогнозу,
				0,95156	388,8353		387,520252	-17,5203	0,047352
			1,072166	382,4036		444,7958933	-34,7959	0,084868
		1,07837	1,102209	390,1258		465,6473151	-35,6473	0,082901
		0,864865	0,874066	411,8682		375,9161901	-15,9162	0,044212
			0,957265	0,95156	441,3806		416,4858429	3,514157	0,008367
		1,09589	1,072166	466,3459		477,4327411	22,56726	0,045135
		1,11828	1,102209	471,78		499,1986767	20,80132	0,040003
		0,874667	0,874066	469,0721		402,5228666	7,477133	0,018237
			0,933687	0,95156	462,3987		445,4514339	-5,45143	0,01239
		1,076517	1,072166	475,6728		510,0695889	-0,06959	0,000136
		1,104167	1,102209	480,8527		532,7500384	-2,75004	0,005189
		0,861538	0,874066	480,5129		429,1295432	-9,12954	0,021737
			0,974619	0,95156	504,435		474,4170248	5,582975	0,011631
		1,065327	1,072166	494,3266		542,7064367	-12,7064	0,023974
		1,091811	1,102209	498,9981		566,3014001	-16,3014	0,029639
		0,8523	0,874066	503,3944		455,7362197	-15,7362	0,035764
			0,955504	0,95156	535,9622		503,3826157	6,617384	0,012975
		1,100917	1,072166	559,6151		575,3432846	24,65672	0,041095
		1,119639	1,102209	562,5069		599,8527618	20,14724	0,032496
		0,817778	0,874066	526,276		482,3428963	-22,3429	0,048572
			0,986784	0,95156	588,5075		532,3482066	27,65179	0,049378
		1,066667	1,072166	578,2689		607,9801324	12,01987	0,019387
		1,07563	1,102209	580,6523		633,4041235	6,595877	0,010306
		0,914761	0,874066	629,243		508,9495728	41,05043	0,074637
			0,95082	0,95156	609,5256		561,3137976	18,6862	0,032218
		1,059063	1,072166	606,2496		640,6169802	9,38302	0,014435
		1,105691	1,102209	616,9431		666,9554851	13,04451	0,019183
		0,869215	0,874066	617,8022		535,5562494	4,443751	0,008229
			0,954274	0,95156	630,5437		590,2793885	9,720612	0,016201
		1,066667	1,072166	634,2304		673,253828	6,746172	0,009921
		1,100775	1,102209	644,1612		700,5068468	9,493153	0,013371
		0,894027	0,874066	663,5654		562,1629259	17,83707	0,030754
			0,948375	0,95156	651,5618		619,2449794	0,755021	0,001218
		1,045455	1,072166	643,5573		705,8906759	-15,8907	0,02303
		1,112782	1,102209	671,3793		734,0582085	5,941791	0,008029
		0,892193	0,874066	686,4469		588,7696025	11,2304	0,018717
			0,93945	0,95156	672,58		648,2105703	-8,21057	0,012829
		1,061818	1,072166	680,865		738,5275237	-8,52752	0,011682
		1,111913	1,102209	698,5973		767,6095702	2,39043	0,003104
		0,887299	0,874066	709,3285		615,376279	4,623721	0,007458

Продовження табл. 7.7

			0,93617	0,95156	693,5981		677,1761613	-17,1762	0,026024
		1,070423	1,072166	708,8457		771,1643715	-11,1644	0,01469
		1,104895	1,102209	716,7427		801,1609319	-11,1609	0,014128
		0,885813	0,874066	732,2101		641,9829556	-1,98296	0,003098
			0,929915	0,95156	714,6162		706,1417522	-26,1418	0,038444
		1,084746	1,072166	746,1534		803,8012193	-3,80122	0,004752
			1,102209	743,9608		834,7122936	-14,7123	0,017942
			0,874066	755,0916		668,5896321	-8,58963	0,013015
				0,95156			735,1073431
			1,072166			836,4380672
			1,102209			868,2636552
			0,874066			695,1963087

Порівнюючи розрахункові значення критеріїв з табличними (a = 0,05), можна зробити висновок про те, що модель тренду, яка описується лінійним рівнянням регресії є адекватною, а оцінки коефіцієнтів рівняння регресії - статистично значущими.

Отже, прогнозна модель з мультиплікативною компонентою має вигляд:

.

Прогнозні значення квартальних випусків твердих сирів за мультиплікативною моделлю становлять (табл.7.7):

= 735 (тис.грн.);

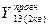= 836 (тис.грн.);

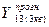= 868 (тис.грн.);

= 695 (тис.грн.).

Середня відносна похибка прогнозування за ретроспективними даними для мультиплікативної моделі складає 2,42%.

Із аналізу і порівняння відносних похибок прогнозування можна зробити висновок, що обидві моделі з практичного погляду є задовільними, проте мультиплікативна модель є точнішою. Відзначимо також, що у наведених моделях не відображено дію цінового чинника, що потребує додаткового дослідження. Можна вважати, що обсяги виробництва продукції виражені не у поточних, а в порівняльних цінах першого року.

Дата добавления: 2014-12-16