Примеры применения теоремы Гаусса 1 страница

1. Напряженность электростатического поля, создаваемого равномерно заряженной сферической поверхностью.

Пусть сферическая поверхность радиуса R (рис. 13.7) несет на себе равномерно распределенный заряд q, т.е. поверхностная плотность 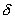заряда в любой точке сферы будет одинакова.

a. Заключим нашу сферическую поверхность в симметричную поверхность S с радиусом r>R. Поток вектора напряженности через поверхность S будет равен

По теореме Гаусса

Следовательно

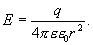
(13.8)

Сравнивая это соотношение с формулой для напряженности поля точечного заряда, можно прийти к выводу, что напряженность поля вне заряженной сферы такова, как если бы весь заряд сферы был сосредоточен в ее центре.

b. Для точек, находящихся на поверхности заряженной сферы радиуса R, по аналогии с вышеприведенным уравнением, можно написать

(13.9)

c. Проведем через точку В, находящуюся внутри заряженной сферической поверхности, сферу S радиусом г<R. Внутри сферы S зарядов нет, т.к. все они расположены на внешней сферической поверхности, т.е. Следовательно, по теореме Гаусса, и напряженность электростатического поля внутри полой равномерно заряженной сферы будет равна нулю. Зависимость напряженности поля заряженной сферы от расстояния r приведена на рис. 13.8.

2. Электростатическое поле шара.

Пусть имеем шар радиуса R, равномерно заряженный с объемной плотностью.

В любой точке А, лежащей вне шара на расстоянии r от его центра (r>R), его поле аналогично полю точечного заряда , расположенного в центре шара. Тогда вне шара

(13.10)

а на его поверхности (r=R)

(13.11)

В точке В, лежащей внутри шара на расстояний r от его центра (r>R), поле определяется лишь зарядом 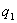, заключенным внутри сферы радиусом r. Поток вектора напряженности через эту сферу равен

с другой стороны, в соответствии с теоремой Гаусса

Из сопоставления последних выражений следует

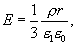
(13.12)

где - диэлектрическая проницаемость внутри шара. Зависимость напряженности поля, создаваемого заряженной сферой, от расстояния до центра шара приведена на (рис.13.10)

3. Напряженность поля равномерно заряженной бесконечной прямолинейной нити (или цилиндра).

Предположим, что полая цилиндрическая поверхность радиуса R заряжена с постоянной линейной плотностью .

Проведем коаксиальную цилиндрическую поверхность радиуса Поток вектора напряженности через эту поверхность

По теореме Гаусса

Из последних двух выражений определяем напряженность поля, создаваемого равномерно заряженной нитью:

(13.13)

4. Напряженность поля, создаваемого, бесконечной равномерно заряженной плоскостью.

Пусть плоскость имеет бесконечную протяженность и заряд на единицу площади равен σ. Из законов симметрии следует, что поле направлено всюду перпендикулярно плоскости, и если не существует никаких других внешних зарядов, то поля по обе стороны плоскости должны быть одинаковы. Ограничим часть заряженной плоскости воображаемым цилиндрическим ящиком, таким образом, чтобы ящик рассекался пополам и его образующие были перпендикулярны, а два основания, имеющие площадь S каждое, параллельны заряженной плоскости (рис 1.10).

Суммарный поток вектора; напряженности равен вектору , умноженному на площадь S первого основания, плюс поток вектора через противоположное основание. Поток напряженности через боковую поверхность цилиндра равен нулю, т.к. линии напряженности их не пересекают. Таким образом, С другой стороны по теореме Гаусса

Следовательно

но тогда напряженность поля бесконечной равномерно заряженной плоскости будет равна

(13.14)

В это выражение не входят координаты, следовательно электростатическое поле будет однородным, а напряженность его в любой точке поля одинакова.

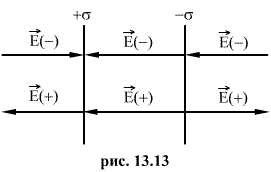
5. Напряженность поля, создаваемого двумя бесконечными параллельными плоскостями, заряженными разноименно с одинаковыми плотностями.

Как видно из рисунка 13.13, напряженность поля между двумя бесконечными параллельными плоскостями, имеющими поверхностные плотности зарядов и , равны сумме напряженностей полей, создаваемых пластинами, т.е.

Таким образом,

(13.15)

Вне пластины векторы от каждой из них направлены в противоположные стороны и взаимно уничтожаются. Поэтому напряженность поля в пространстве, окружающем пластины, будет равна нулю Е=0.

5. Работа по перемещению заряда в электрическом поле. Циркуляция вектора напряженности электрического поля.

Элементарная работа, совершаемая силой F при перемещении точечного электрического заряда из одной точки электростатического поля в другую на отрезке пути 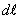, по определению равна

где - угол между вектором силы F и направлением движения 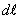. Если работа совершается внешними силами, то dA0. Интегрируя последнее выражение, получим, что работа против сил поля при перемещении пробного заряда из точки “а” в точку “b” будет равна

где 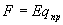- кулоновская сила, действующая на пробный заряд в каждой точке поля с напряженностью Е. Тогда работа

Пусть заряд перемещается в поле заряда q из точки “а”, удалённой от q на расстоянии в точку “b”, удаленную от q на расстоянии 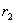(рис 1.12).

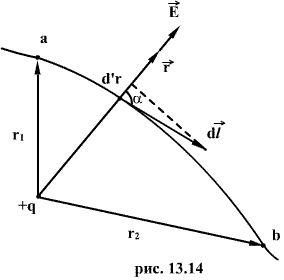
Как видно из рисунка тогда получим

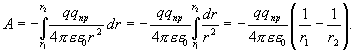
Как было сказано выше, работа сил электростатического поля, совершаемая против внешних сил, равна по величине и противоположна по знаку работе внешних сил, следовательно

Циркуляцией вектора напряженности называется работа, которую совершают электрические силы при перемещении единичного положительного заряда по замкнутому пути L

(13.18)

Так как работа сил электростатического поля по замкнутому контуру равна нулю (работа сил потенциального поля), следовательно циркуляция напряженности электростатического поля по замкнутому контуру равна нулю.

6. Потенциал. Разность потенциалов. Эквипотенциальные поверхности.

Внося в данную точку поля различные пробные заряды мы будем, соответственно, изменять потенциальную энергию, т.е. получим различные . Но отношение потенциальной энергии к заряду остается величиной постоянной. Следовательно для характеристики поля можем использовать это отношение. Обычно оно обозначается буквой 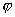и называется потенциалом поля в данной точке

(13.19)

Потенциал является энергетической характеристикой поля. Он численно равен работе, которую надо затратить против сил электрического поля при перенесении единичного положительного точечного заряда из бесконечности в данную точку поля. Единица измерения потенциала - вольт. С учетом (1.16)

(13.20)

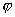Когда поле образовано несколькими произвольно расположенными зарядами , потенциал его в данной точке равен алгебраической сумме потенциалов , создаваемых каждым зарядом в отдельности, т.е.

(13.21)

Если из точки “а” в точку “b” электрического поля перемещается заряд q’, то при этом совершается работа против электрических сил, равная

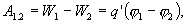
где 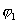и - потенциалы поля в точках “а” и ” b”.

В СИ за единицу разности потенциалов принимают Вольт (В), Разность потенциалов между двумя точками поля равна одному Вольту, если для перемещения между ними заряда в один Кулон нужно совершить работу в один Джоуль

В атомной физике и электронике часто употребляют для измерения работы и энергии, величину называемую электронвольтом (эВ). Один электронвольт равен работе, совершаемой при перемещении заряда, равного заряду электрона, между двумя точками поля с разностью потенциалов один вольт.

1. Электрическое поле сферической поверхности радиуса R.

a. Разность потенциалов между двумя точками, лежащими на расстоянии и 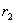от центра заряженной сферической поверхности , находим из формулы

Интегрируя левую и правую части этого уравнения

получим

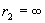b. Положив и , получим потенциал заряженной сферической поверхности

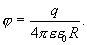
c. Внутри заряженной сферы поля нет, и потому весь ее объём эквипотенциален, т.е.

и

и равен потенциалу на поверхности (при r=R).

2. Потенциал электрического поля плоскости.

Найдем разность потенциалов между двумя точками М и N, лежащими на расстоянии и 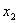от плоскости. , Но для плоскости , поэтому

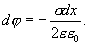
Проинтегрировав последнее выражение по х от до 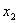и обозначив потенциал в точках М и N через 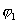и , получим

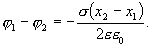
3. Разность потенциалов между двумя параллельными плоскостями

Находящимися на расстоянии а друг от друга, найдем аналогичным путем:

, или (с учетом 13.15)

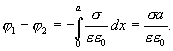
4. Электрическое поле бесконечного длинного прямого кругового цилиндра.

Воспользуемся, как прежде, связью потенциала с напряженностью и уравнением (13.13):

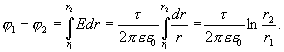
7. Связь между напряженностью поля и потенциалом.

Из выше сказанного следует, что электрическое поле характеризуется двумя физическими величинами: напряженностью (силовая характеристика) и потенциалом (энергетическая характеристика). Выясним как они связаны между собой. Пусть положительный заряд q перемещается силой электрического поля с эквипотенциальной поверхности, имеющей потенциал , на близко расположенную эквипотенциальную поверхность, имеющую потенциал 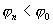(рис. 13.16).

Напряженность поля Е на всем малом пути dx можно считать постоянной. Тогда работа перемещения С другой стороны . Из этих уравнений получаем

(13.22)

Знак минус обусловлен тем, что напряженность поля направлена в сторону убывания потенциала, тогда как градиент потенциала направлен в сторону возрастания потенциала.

8. Диэлектрики в электростатическом поле. Поляризация диэлектриков.

Свободные заряды, имеющиеся в любом проводнике, перемещаются под действием внешнего электрического поля и спустя очень малый промежуток времени создают поле, полностью компенсирующее внешнее. Поэтому напряженность электрического поля внутри проводника (при отсутствии тока) равна нулю.

Термин “диэлектрики” был введен Фарадеем. Диэлектриком является любая среда (газ, жидкость или твердое тело), в которой длительное время может существовать электрическое поле. В отличие от проводников в диэлектриках отсутствуют свободные электрические заряды. Т.е. диэлектриками называют тела в которых заряды не могут перемещаться из одной части в другую.

Атомы и молекулы диэлектрика содержат равные количества положительных и отрицательных микроскопических зарядов и в целом электрически нейтральны. В зависимости от строения все диэлектрические вещества можно разделить на три большие группы.

1. К первой группе принадлежат диэлектрики, состоящие из молекул, у которых “центры тяжести” положительных и отрицательных зарядов совпадают (например, бензол и др). Молекулы таких диэлектриков в отсутствие внешнего электрического поля не обладают дипольным моментом (рис.14.1.а). Во внешнем электрическом поле “центы тяжести” положительных и отрицательных (электронных оболочек) зарядов молекулы смещаются в противоположные стороны на некоторое расстояние L, малое по сравнению с размерами молекулы (рис.14.1 б). Каждая молекула при этом становится полярной (дипольной), подобной электрическому диполю и приобретает дипольный электрический момент Такого рода поляризация называется электронной. При помещений диэлектрика в электрическое поле все неполярные молекулы превращаются в дипольные, расположенные цепочками вдоль силовых линий поля (рис.14.2). В результате торцы диэлектрика приобретают разноименные заряды - диэлектрик поляризуется. Степень электронной поляризации зависит от его свойств и от величины напряженности поля .

2. Вторую группу диэлектриков составляют такие вещества, как вода, нитробензол и др. В таких веществах молекулы всегда (ив отсутствие внешнего поля) несимметричны, т.е. являются дипольными. Благодаря тепловому движению дипольные молекулы расположены в диэлектрике беспорядочно (рис.14.3 а). Поэтому диэлектрик в целом оказывается не поляризованным. Под влиянием электрического поля все дипольные молекулы диэлектрика повернутся так, что их оси расположатся приблизительно вдоль силовых линий поля (рис.14.3 б). Такого рода поляризация называется ориентационной или дипольной поляризацией. Полной ориентации препятствует тепловое движение.

3. К третьей группе относятся кристаллические диэлектрики, имеющие ионное строение (хлористый натрий, хлористый калий и др). У кристаллических диэлектриков с ионной решеткой каждая пара соседних разноименных ионов подобна диполю (рис. 14.4.а) В электрическом поле эти диполи деформируются: удлиняются, если их оси направлены по полю, и укорачиваются, если оси направлены против поля. В результате диэлектрик поляризуется. Введем величину, характеризующую степень поляризации диэлектрика. Если просуммировать все дипольные моменты диэлектрика в единице объема, то получим вектор поляризации

Для определения степени поляризации в точке необходимо ΔV устремить к нулю. Вектор направлен вдоль электрического поля , в котором находится диэлектрик. Для не слишком сильных полей можно принять, что величина вектора поляризации пропорциональна величине напряженности поля, т.е. Р~Е

В системе СИ вектор поляризации

(14.1)

где - называется диэлектрической восприимчивостью вещества и зависит от его строения.

9. Вектор поляризации. Напряженность поля в диэлектриках. Связь вектора поляризации с поверхностной плотностью связанных зарядов.

Рассмотрим диэлектрическую пластинку, заполняющую плоский конденсатор (рис.14.5) и находящуюся, следовательно, в практически однородном внешнем поле .

В результате поляризации на гранях диэлектрика, обращенных к пластинам конденсатора, концы молекулярных диполей окажутся нескомпенсированными соседними диполями. Поэтому на правой грани, обращенной к отрицательной пластине конденсатора, окажется избыток положительного заряда с некоторой поверхностной плотностью 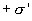. На противоположной стороне диэлектрика . Эти так называемые поляризационные, или связанные заряды не могут быть переданы соприкосновением другому телу без разрушения молекул диэлектрика, т.к. они обусловлены самими поляризованными молекулами. Возникновение поляризованных зарядов приводит к возникновению дополнительного электрического поля , направленного против внешнего поля . Результирующее электрическое поле Е внутри диэлектрика равно

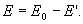
(14.2)

Для определения применим формулу вычисления напряженности конденсатора

(14.3)

Свяжем 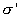с вектором поляризации Р. Для этого определим полный дипольный момент (во всем объеме) диэлектрика. Осуществим это двумя способами:

С одной стороны Р по определению дипольный момент единицы объема и если умножим на V, получим полный дипольный момент

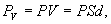
(14.4)

где S - площадь пластины конденсатора.

С другой стороны рассмотрим диэлектрик как большой диполь, у которого с одной стороны заряд , а с другой 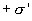и расстояние d. Отсюда

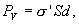
(14.5)

Приравнивая (14.4) и (14.5), получим

Подставляя 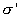в (14.3), и затем результат в (14.2), получим

Подставим значение Р из выражения (14.1), тогда

(14.6)

Величина

(14.7)

называется диэлектрической проницаемостью или относительной диэлектрической проницаемостью. Диэлектрическая проницаемость показывает во сколько раз уменьшается напряженность в диэлектрике по сравнению с напряженностью в вакууме. и , т.е. с ростом температуры диэлектрические свойства ухудшаются.

10. Теорема Остроградского-Гаусса для поля в диэлектриках.

Согласно принципу суперпозиции полей, напряженность поля в диэлектрике равна геометрической сумме напряженностей полей свободных и связанных зарядов

.

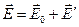Теорема Остроградского-Гаусса для электростатического поля в вакууме может быть распространена на электростатическое поле в среде, если под понимать алгебраическую сумму всех свободных и связанных зарядов, охватываемых замкнутой поверхностью .

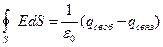(8)

(9)

Подставим (9) в (8)

-

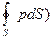
или

.

В обоих интегралах интегрирование проводится по одной и той же замкнутой поверхности . Поэтому

Вектор

(10)

называется электрическим смещением. Размерность [D]=Кл/м ². Тогда теорема Остроградского-Гаусса для электростатического поля в диэлектрике запишется в форме

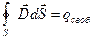. (11)

Дата добавления: 2014-12-16