Примеры применения теоремы Гаусса 2 страница

Поток электрического смещения электростатического поля сквозь произвольную замкнутую поверхность, проведенную в поле, равен алгебраической сумме свободных зарядов, охватываемых этой поверхностью.

При расчете полей в среде удобней пользоваться электрическим смещением 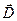, так как оно в отличие от напряженности поля 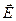не испытывает скачкообразные изменения при переходе через границу диэлектриков.

11. Сегнетоэлектрики.

егнетоэлектрики — диэлектрики, которые обладают в определенном интервале температур спонтанной (самопроизвольной) поляризованностью, т. е. поляризованностью в условиях отсутствия внешнего электрического поля. К сегнетоэлектрикам относятся, например, подробно изученные И. В. Курчатовым (1903—1960) и П. П. Кобеко (1897—1954) сегнетова соль NaKC₄H₄O₆•4Н₂O (от нее и было получено данное название) и титанат бария ВаТiO₃.

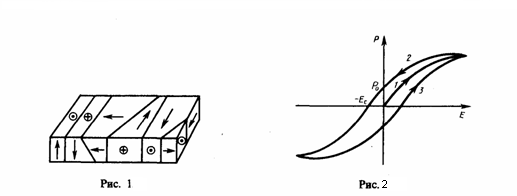
При отсутствии внешнего электрического поля сегнетоэлектрик есть как бы мозаика из доменов — областей с различными направлениями поляризованности. Это показано на примере титаната бария (рис. 1), где стрелки и знаки точек и плюсов в кружках указывают направление вектора Р. Так как в смежных доменах эти направления отличаются, то в целом дипольный момент диэлектрика равен нулю. При внесении во внешнее поле сегнетоэлектрика осуществляется переориентация дипольных моментов доменов по полю, а возникшее при этом суммарное электрическое поле доменов будет поддерживать их некоторую ориентацию и после прекращения действия внешнего поля. Поэтому сегнетоэлектрики имеют очень большие значения диэлектрической проницаемости (для сегнетовой соли, например, ε_max≈10⁴).

Сегнетоэлектрические свойства вществ сильно зависят от температуры. Для каждого сегнетоэлектрика есть определенная температура, выше которой его данные необычные свойства исчезают и он превращается в обычный диэлектрик. Эта температура называется точкой Кюри (в честь французского физика Пьера Кюри (1859—1906)). Обычно, сегнетоэлектрики обладают только одной точкой Кюри; исключение составляют лишь сегнетова соль (—18 и +24°С) и изоморфные с нею соединения. В сегнетоэлектриках вблизи точки Кюри наблюдается также резкое возрастание теплоемкости вещества. Превращение сегнетоэлектриков в обычный диэлектрик, которое происходит в точке Кюри, сопровождается фазовым переходом II рода.

Диэлектрическая проницаемость ε (а значит, и диэлектрическая восприимчивость θ) сегнетоэлектриков зависит от напряженности Е поля в веществе, при этом эти величины являются характеристиками вещества для других диэлектриков.

Для сегнетоэлектриков не соблюдается формула связи поляризованности и напряженности поля P =θε₀ E; для них зависимость между векторами поляризованности (Р) и напряженности (Е) нелинейная и зависит от значений Е в предыдущие моменты времени. В сегнетоэлектриках наблюдается явление диэлектрического гистерезиса (запаздывания). Как видно из рис. 2, с ростом напряженности Е внешнего электрического поля поляризованность Р растет, достигая при этом насыщения (кривая 1). Уменьшение Р с уменьшением Е происходит по кривой 2, и при Е=0 сегнетоэлектрик сохраняет остаточную поляризованность Р₀, т.е. сегнетоэлектрик остается поляризованным в отсутствие внешнего электрического поля. Чтобы уничтожить остаточную поляризованность, надо приложить внешнее электрическое поле обратного направления (—E_с). Величина Е_c называется коэрцитивной силой (от лат. coercitio — удерживание). Если далее Е изменять, то Р изменяется по кривой 3 петли гистерезиса.

Росту изучения сегнетоэлектриков послужило открытие аномальных диэлектрических свойств титаната бария академиком Б. М. Вулом (1903—1985). Титанат бария из-за его высокой механической прочности и химической устойчивости, а также по причине сохранения сегнетоэлектрических свойств в широком температурном интервале нашел широкое научно-техническое применение (например, в качестве приемника и генератора ультразвуковых волн). В настоящее время известно более сотни сегнетоэлектриков, не считая их твердых растворов. Сегнетоэлектрики широко используются также в качестве материалов, которые обладают большими значениями ε (например, в конденсаторах).

Следует кратко рассказать еще о пьезоэлектриках — кристаллических веществах, в которых при растяжении или сжатии в некоторых направлениях возникает электрическая поляризация даже в отсутствие внешнего электрического поля (прямой пьезоэффект). Можно наблюдать и обратный пьезоэффект — появление механической деформации под действием электрического поля. У некоторых пьезоэлектриков в состоянии термодинамического равновесия решетка положительных ионов смещена относительно решетки отрицательных ионов, в результате чего они оказываются поляризованными даже в отсутствии внешнего электрического поля. Такие кристаллы называются пироэлектриками. Еще существуют электреты — диэлектрики, которые длительно сохраняют поляризованное состояние после снятия внешнего электрического поля (электрические аналоги постоянных магнитов). Эти вещества находят широкое применение в технике и бытовых устройствах.

12.Проводники в электростатическом поле. Электростатическая индукция.

Если проводник поместить во внешнее электростатическое поле или зарядить его, то на заряды данного проводника будет действовать электростатическое поле, под действием которого они начнут двигаться. Движение зарядов (ток) будет длиться до тех пор, пока не установится равновесное распределение зарядов, при котором электростатическое поле внутри данного проводника обращается в нуль. Это происходит в течение очень короткого времени. Действительно, если бы поле не было равно нулю, то в проводнике появилось бы упорядоченное движение зарядов без затраты энергии от внешнего источника, что не согласуется с законом сохранения энергии. Значит, напряженность поля во всех точках внутри проводника равна нулю:

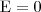
Если внутри проводника электрического поле отсутствует, то потенциал во всех точках внутри проводника одинаков (φ = const), т. е. поверхность проводника в электростатическом поле является эквипотенциальной. Это означает, что вектор напряженности поля на внешней поверхности проводника направлен по перпендикуляру к каждой точке его поверхности. Если это было бы не так, то под действием касательной составляющей Е заряды начали бы перемещаться по поверхности проводника, что, в свою очередь, противоречило бы равновесному распределению зарядов.

Если проводнику дать некоторый дополнительный заряд Q, то нескомпенсированные заряды разместяться только на поверхности проводника. Это вытекает непосредственно из теоремы Гаусса, согласно которой заряд Q, который находится внутри проводника в некотором объеме, ограниченном произвольной замкнутой поверхностью, равен

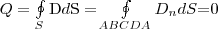
поскольку во всех точках внутри замкнутой поверхности D=0.

Теперь мы будем искать взаимосвязь между напряженностью Е поля вблизи поверхности заряженного проводника и поверхностной плотностью зарядов на его поверхности σ. Для этого используем теорему Гаусса для бесконечно малого цилиндра с основаниями ΔS, который пересекает границу проводник—диэлектрик. Ось цилиндра направлена вдоль вектора Е (рис. 1). Поток вектора электрического смещения через внутреннюю часть цилиндрической поверхности равен нулю, так как внутри проводника Е₁ (а следовательно, и D₁) есть нуль, поэтому поток вектора D сквозь замкнутую цилиндрическую поверхность определяется только потоком сквозь наружное основание цилиндра. Используя теорему Гаусса, этот поток (DΔS) равен сумме зарядов (Q=σΔS), находящихся внутри поверхности: DΔS=σΔS т.е.

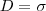(1)

или

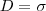(2)

где ε — диэлектрическая проницаемость среды, находящаяся вокруг проводника.

Значит, напряженность электростатического поля у поверхности проводника задается поверхностной плотностью зарядов. Можно показать, что формула (2) задает напряженность электростатического поля вблизи поверхности проводника абсолютно произвольной формы.

Если во внешнее электростатическое поле поместить нейтральный проводник, то свободные заряды (электроны, ионы) будут совершать движение: положительные — по полю, отрицательные — против поля (рис. 2, а). На одном конце проводника будет собираться избыток положительного заряда, на другом — избыток отрицательного заряда. Эти заряды называются индуцированными (наведенными). Процесс будет продолжаться до тех пор, пока внутри проводника напряженность поля не станет равной нулю, а линии напряженности вне проводника — перпендикулярными его поверхности (рис. 2, б). Значит, нейтральный проводник, который внесен в электростатическое поле, разрывает часть линий напряженности; эти линии напряженности заканчиваются на отрицательных индуцированных зарядах и вновь начинаются на положительных. Индуцированные заряды распределяются на внешней поверхности нашего проводника. Явление перераспределения поверхностных зарядов на проводнике во внешнем электростатическом поле называется электростатической индукцией.

Из рис. 2, б мы видим, что индуцированные заряды образуются на проводнике вследствие смещения их под действием поля, т. е. σ есть поверхностной плотностью смещенных зарядов. Согласно (1), электрическое смещение D вблизи проводника численно равно поверхностной плотности смещенных зарядов. По этой причине вектор D получил название вектора электрического смещения.

Поскольку в состоянии равновесия заряды отсутствуют внутри проводника, то создание внутри него полости не окажет влияния на конфигурацию расположения зарядов и тем самым на электростатическое поле. Значит, поле будет отсутствовать внутри полости. Если теперь заземлить данный проводник с полостью, то потенциал во всех точках полости будет равен нулю, т. е. полость полностью является изолированной от влияния внешних электростатических полей. На этом основана электростатическая защита — экранирование тел, например измерительных приборов, от влияния внешних электростатических полей. Для защиты вместо сплошного проводника может быть использована густая металлическая сетка, которая, также эффективна при наличии не только постоянных, но и переменных электрических полей.

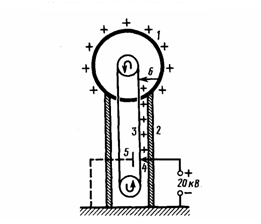
Свойство зарядов располагаться на внешней поверхности проводника на практике используется для устройства электростатических генераторов, которые предназначены для накопления больших зарядов и достижения разности потенциалов в несколько миллионов вольт. Электростатический генератор, который изобретен американским физиком Р. Ван-де-Граафом (1901—1967), состоит из шарообразного полого проводника 1 (рис. 3), укрепленного на изоляторах 2. Движущаяся замкнутая лента 3 из прорезиненной ткани заряжается от источника напряжения с помощью системы остриев 4, которые соединены с одним из полюсов источника, второй полюс которого заземлен. Заземленная пластина 5 усиливает стекание зарядов с остриев на ленту. Другая система остриев 6 снимает заряды с ленты и передает их полому шару, и они переходят на его внешнюю поверхность. Значит, сфера постепенно получает большой заряд и удается достичь разности потенциалов в несколько миллионов вольт. Электростатические генераторы широко применяются в высоковольтных ускорителях заряженных частиц, а также в слаботочной высоковольтной технике.

ЭЛЕКТРОСТАТИЧЕСКАЯ ИНДУКЦИЯ - перераспределение зарядов на поверхности проводника или поляризация диэлектрика под действием стороннего электрич. поля E _ст(r). Вследствие Э. и. у электрически нейтральных (в целом) тел появляется индуцированный электрич. диполь-ный момент р ^е и, в общем случае, более высокие моменты: квадрупольный, октупольный и т. д. (см. Мультиполи). Для металлич. шара, радиус к-рого а мал по сравнению с масштабом неоднородности поля, р ^е = а ³ E _сг, для диэлек-трич. шара p ^е = а ³ [(e- l)/(e + 2)] E _ст (в электростатике ди-электрич. проницаемость e>=1). На несимметричные тела в общем случае действует момент сил M = [ p ^e E _cт], разворачивая их до тех пор, пока р ^e не станет параллельным электрич. полю: р ^e a E _ст, a>0. Так, вытянутые объекты (иглы, нити, молекулярные цепочки) ориентируются вдоль силовых линий поля. Др. эффектом Э. и. является втягивание частиц в область сильных полей под действием силы F =( p ^e ) E _ст=(l/2)a 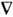| E _ст|². Этим объясняется интенсивное оседание пыли на наэлектризованных деталях телевизоров, ткацких машин и т. д. На явлении Э. и. основаны принципы работы эл--статич. фильтров, эл--графич. машин, эл--статич. сепараторов молекул

13.Электроемкость проводников. Взаимная емкость. Конденсаторы.

Сообщенный проводнику заряд q распределяется по его поверхности так, чтобы напряженность поля внутри проводника была равна нулю. Если проводнику, уже несущему заряд q, сообщить еще заряд той же величины, то второй заряд должен распределиться по проводнику точно также, как и первый, в противном случае он создает в проводнике поле, не равное нулю. Таким образом, различные по величине заряды распределяются на удаленном от других тел (уединенном) проводнике подобным образом, т.е. отношение плотностей заряда в двух произвольных точках поверхности проводника при любой величине заряда будет одно и то же.

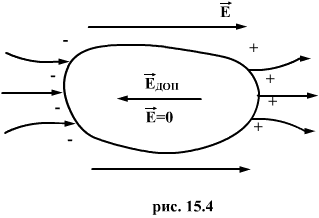
Отсюда вытекает, что потенциал уединенного проводника пропорционален находящемуся на нем заряду. Действительно, увеличение в некоторое число раз заряда приводит к увеличению в тоже число раз напряженности поля в каждой точке окружающего проводника пространства, т.е.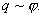

Вводя соответствующий коэффициент пропорциональности, запишем 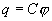или

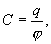
(15.2)

где С - называется электроемкостью.

Таким образом, электроемкость уединенного проводника есть физическая величина численно равная величине заряда, который необходимо сообщить данному проводнику для увеличения его потенциала на единицу. В СИ единицей емкости является Фарад (Ф).

Определим электроемкость уединенного шара. Потенциал заряженного шара радиуса R

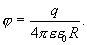
Сравнивая с 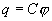получаем

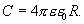
Взаимная емкость.

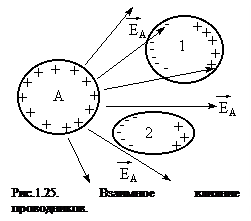
Пусть вблизи заряженного проводника А нахо­дятся незаряженные проводни­ки или диэлектрики. Под действием поля проводника А в телах 1 и 2 возни­кают индуцированные (если 1 и 2 проводники) или свя­занные (если диэлектрики) заряды, причем ближе к А будут располагаться заряды противоположного знака (рис.1.25). Индуцированные (или связанные) заряды соз­дают свое поле противоположного на­правления, чем ослабляют поле проводника А, уменьшая его потенциал и увеличи­вая его электроемкость.

На практике существует потребность в устройствах, которые при относитель­но небольшом потенциале накапливали (конденсировали) бы на себе заметные по вели­чине заряды. В основу таких устройств, называемых конденсаторами, поло­жен факт, что емкость проводника возрастает при приближении к нему других тел. Простейший плоский конденсатор состоит из двух близко расположенных про­водников, заряженных равными по величине и противоположными по знаку заряда­ми. Образующие данную систему проводники называются обкладка­ми.

Для того, чтобы поле, создаваемое заряженны­ми обкладками, было полностью сосредоточено внутри конденсатора, обкладки должны быть в виде двух близко рас­положенных пластин, или коаксиаль­ных цилиндров, или концентрических сфер. Со­ответ­ственно конденсаторы называются плоскими, цилиндрическими или сфериче­скими.

Разность потенциалов между обкладками пропорциональна абсолютной вели­чине заряда обкладки. Поэтому отношение 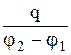есть величина постоянная для конкретного кон­денсатора. Она обозначается С и называется взаимной электроемкостью провод­ников или емкостью конденсатора. Емкость конденсатора численно равна заряду, который нужно перенести с одной обкладки конденсатора на другую, чтобы изме­нить разность их потенциалов на единицу.

Разность потенциалов плоского конденсатора равна 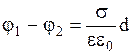, где 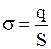поверхностная плотность заряда обкладки. S - площадь обкладки конденса­тора.. Отсюда емкость плоского конденсатора 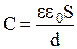. Из этой формулы следует, что С плоского конденсатора зави­сит от его геометрических размеров, т.е. от S и d, и диэлектри­ческой проницаемости диэлектрика, заполняющего межплоско­стное пространство. Применение в качестве прослойки сегнетоэлектриков значительно увеличива­ет емкость конденсатора, т.к. e у них достигает очень больших значений. В очень сильных полях (порядка Е_пр»10⁷ В/м) происходит разруше­ние диэлектрика или «пробой», он перестает быть изо­ля­тором и становится проводником. Это «пробивное напряжение» зависит от формы обкладок, свойств диэлектрика и его толщины..

Для получения устройств различной электроемкости конденсаторы соединяют парал­лельно и после­довательно.

Параллельное соединение конденсаторов (Рис. 1. 26). В данном случае, так как соединенные провода-проводники имеют один и тот же потенциал, то разность потенциалов на обкладках всех конденсаторов оди­накова и равна 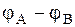. Заряды конденсаторов будут

, …, .

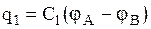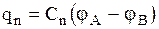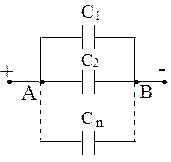Рис.1.26. Параллельное соединение конденса­торов.

Заряд, запасенный всей батареей .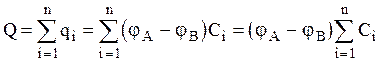

Отсюда видно, что полная емкость системы из параллельно соединенных конденсаторов 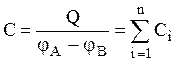равна сумме емкостей всех конденсаторов.

Последовательное соединение конденсаторов (Рис. 1. 27). В данном случае, вследствие электростатической индукции, заряды на всех обкладок q будут равны по мо­дулю, а общая разность потенциалов складывается из разностей на отдельных конденсаторах . Так как 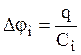, то 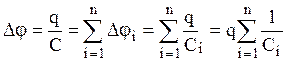. Отсюда .

Рис.1.27. Последовательное соеди­нение конденса­то­ров.

При последовательном сое­динении конденсаторов обратная величина результирующей емкости равна сумме обратных величин емкостей всех конденсаторов.

Для получения устройств, которые при небольшом относительно среды потенциале накапливали бы на себе (конденсировали) заметные по величине заряды используют тот факт, что электроемкость проводника возрастает при приближении к нему других тел. Действительно, под действием поля, создаваемого заряженными проводниками, на поднесенном к нему теле возникают индуцированные (на проводнике) или связанные (на диэлектрике) заряды (рис.15.5). Заряды, противоположные по знаку заряду проводника q располагаются ближе к проводнику, чем одноименные с q, и, следовательно, оказывают большое влияние на его потенциал.

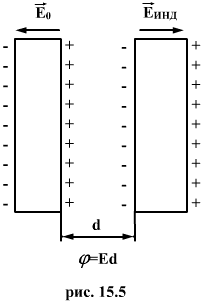
Поэтому при поднесении к заряженному проводнику какого либо тела напряженность поля 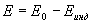уменьшается, а, следовательно, уменьшается потенциал проводника. Согласно уравнение 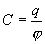это означает увеличение емкости проводника.

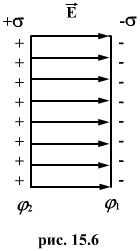
Конденсатор состоит из двух проводников (обкладок) (рис.15.6), разделенных прослойкой диэлектрика. При приложении к проводнику некоторой разности потенциалов его обкладки заряжаются равными по величине зарядами противоположного знака. Под электроемкостью конденсатора понимается физическая величина, пропорциональная заряду q и обратно пропорциональна разности потенциалов между обкладками

Определим емкость плоского конденсатора.

Если площадь обкладки S, а заряд на ней q, то напряженность поля между обкладками

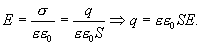
С другой стороны разность потенциалов между обкладками 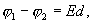откуда

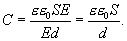
14.Электроемкость плоского, сферического и цилиндрического конденсаторов.

Дата добавления: 2014-12-16