Способы перевода чисел из одной системы счисления в другую

Билет № 4. Перевод чисел в недесятичные системы счисления

Например

Билет № 3. Кодирование и декодирование текстовой информации различными способами

(открыть Word → вставка → символ и выбираете нужные символы и буквы)

1. Закодируйте с помощью кодировочной таблицы ASCII и представь­те в шестнадцатеричной системе счисления следующие тексты:

а) Password; б) Windows; в) Norton Commander.

Ответ:

а) 50 61 73 73 77 6F 72 64;
б) 57 69 6Е 64 6F 77 73;
в) 4С 6F 67 69 6Е.

2. Декодируйте с помощью кодировочной таблицы ASCII следующие тексты, заданные шестнадцатеричным кодом:

а) 54 6F 72 6Е 61 64 6F;
б) 49 20 6С 6F 76 65 20 79 6F 75;
в) 32 2А 78 2В 79 3D 30.

Ответ:

a) Tornado;
б) I love you;
в) 2 * X + Y = 0

3. Декодируйте следующие тексты, заданные десятичным кодом:

а) 087 111 114 100;
б) 068 079 083;
в) 080 097 105 110 116 098 114 117 115 104.

Ответ:

Word VOS Paintbrush

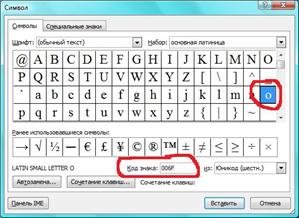
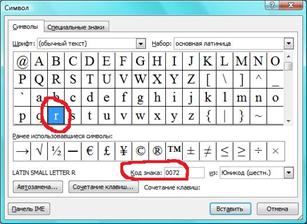
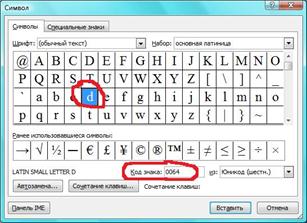
Получилось слово Word (нули не берем). если даны цифры, а нужно узнать слово, то делаем наоборот, смотри код знака и какая это буква.

Перевод чисел из одной позиционной системы счисления в другую: перевод целых чисел.

Чтобы перевести целое число из одной системы счисления с основанием d1 в другую с основанием d2 необходимо последовательно делить это число и получаемые частные на основание d2 новой системы до тех пор, пока не получится частное меньше основания d2. Последнее частное – старшая цифра числа в новой системе счисления с основанием d2, а следующие за ней цифры - это остатки от деления, записываемые в последовательности, обратной их получению. Арифметические действия выполнять в той системе счисления, в которой записано переводимое число.

Пример 2. Перевести число 122(10) в восьмеричную систему счисления.

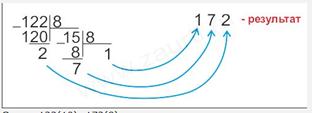
Ответ: 122(10)=172(8).

Пример 3. Перевести число 500(10) в шестнадцатеричную систему счисления.

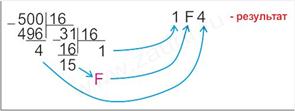
Ответ: 500(10)=1F4(16).

Перевод чисел из одной позиционной системы счисления в другую: перевод правильных дробей.

Чтобы перевести правильную дробь из системы счисления с основанием d1 в систему с основанием d2, необходимо последовательно умножать исходную дробь и дробные части получающихся произведений на основание новой системы счисления d2. Правильная дробь числа в новой системе счисления с основанием d2 формируется в виде целых частей получающихся произведений, начиная с первого.
Если при переводе получается дробь в виде бесконечного или расходящегося ряда, процесс можно закончить при достижении необходимой точности.

При переводе смешанных чисел, необходимо в новую систему перевести отдельно целую и дробную части по правилам перевода целых чисел и правильных дробей, а затем оба результата объединить в одно смешанное число в новой системе счисления.

Пример 2. Перевести число 0,6(10) в восьмеричную систему счисления.

Ответ: 0,6(10)=0,463(8).

Пример 2. Перевести число 0,7(10) в шестнадцатеричную систему счисления.

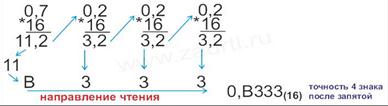
Ответ: 0,7(10)=0,В333(16).

Перевод восьмеричных и шестнадцатеричных чисел в двоичную систему счисления и обратно.

Для перевода числа из восьмеричной системы счисления в двоичную необходимо каждую цифру этого числа записать трехразрядным двоичным числом (триадой).

Для обратного перевода двоичного числа в восьмеричную систему счисления, необходимо исходное число разбить на триады влево и вправо от запятой и представить каждую группу цифрой в восьмеричной системе счисления. Крайние неполные триады дополняют нулями.

Для перевода числа из шестнадцатеричной системы счисления в двоичную необходимо каждую цифру этого числа записать четырехразрядным двоичным числом (тетрадой).

Пример: записать число 7A,7E(16) в двоичной системе счисления.

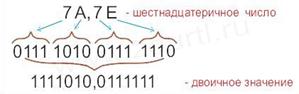
Ответ: 7A,7E(16)= 1111010,0111111(2).

Примечание: незначащие нули слева для целых чисел и справа для дробей не записываются.

Для обратного перевода двоичного числа в шестнадцатеричную систему счисления, необходимо исходное число разбить на тетрады влево и вправо от запятой и представить каждую группу цифрой в шестнадцатеричной системе счисления. Крайние неполные триады дополняют нулями.

Дата добавления: 2014-12-16