Проектування елементарних

ГЕОМЕТРИЧНИХ ФІГУР

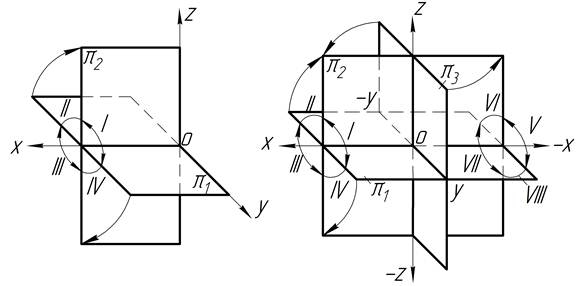
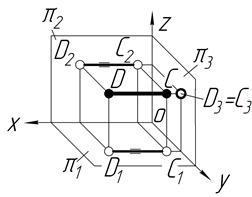
Побудова проекцій геометричних елементів ґрунтується на методі ортогонального паралельного проектування. В ортогональному проектуванні знаходять кілька проекцій оригіналу на взаємно перпендикулярні площини проекцій (рис. 1.1)

а) б)

Рисунок 1.1 – Ортогональна система двох (а) та трьох (б) площин проекцій

Дві площини проекцій ділять весь простір на чотири двогранні кути, які називають квадранти або чверті.

Три координатні площини проекцій ділять весь простір на вісім тригранних кутів, які називають октантами. Знаки координат в октантах представлені в таблиці 1.1.

Таблиця 1.1 – Знаки координат

Октанти	Координати	Октанти	Координати
Х	Y	Z	Х	Y	Z
І ІІ ІІІ ІV	+ + + +	+ - - +	+ + - -	V VI VII VIII	- - - -	+ - - +	+ + - -

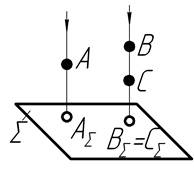
Основні положення проекції точки:

1) прямокутною проекцією точки є основа перпендикуляра, який опущений з даної точки на площину проекцій (рис.1.2);

2) проекцією точки завжди буде точка;

3) кожна точка має тільки одну проекцію на даній площині проекцій;

4)

Рисунок 1.2 ─ Ортогональне проектування точки на площину проекцій

дві точки, розміщені на одному проекційному промені, проектуються в одну точку (рис.1.2).

Одна проекція точки не визначає її положення в просторі відносно площин проекцій, тоді як дві проекції точки визначають положення самої точки відносно площин проекцій.

1.1 Проекція точки на дві площини проекцій, епюр точки

Множина двох (або більше) ортогональних проекцій точки (після суміщення площин проекцій) називається епюром (від французького epure – креслення). Більш загальне визначення епюра: зображення, яке отримуємо при суміщенні площин проекцій. На рисунку 1.3 показано епюр точки А і зображено приклад проектування точки, яка знаходиться в І чверті простору. При суміщенні площин проекцій, проекції точки А (А₁ і А₂) розміщені по обидві сторони від осі ОХ і на одному перпендикулярі до неї. Відстань від проекції А₂ до осі ОХ на епюрі відповідає відстані від точки А до горизонтальної площини проекцій, відстань від проекції А₁ до осі ОХ відповідає відстані від точки А до фронтальної площини проекцій. А₁А₂ - лінія проекційного зв’язку.

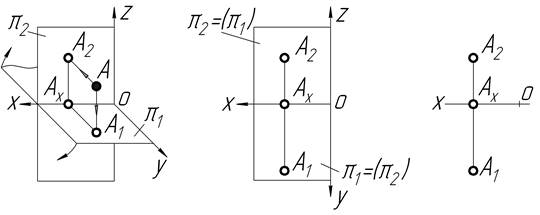
Рисунок 1.3 ─ Послідовність утворення епюру

В таблиці 1.2 зведені приклади епюрів точок, розміщених в І, ІІ, ІІІ, ІV чвертях простору.

Таблиця 1.2 – Точка в чвертях простору

Чверть	Наочне зображення	Епюр
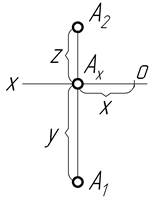
І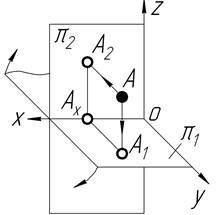
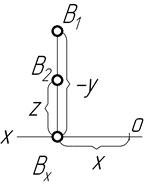
ІІ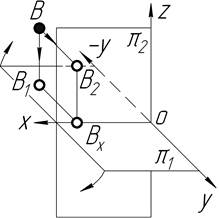
Продовження таблиці 1.2
Чверть	Наочне зображення	Епюр
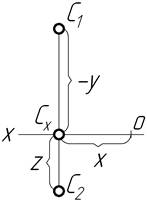
ІІІ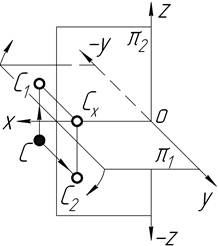
ІV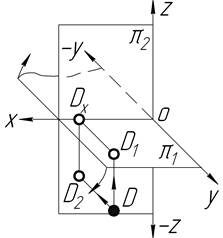

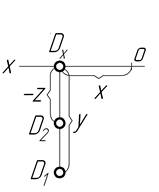
З таблиці 1.2 видно, що точка А знаходиться в просторі І чверті, точка В – в ІІ чверті, точка C – в ІІІ чверті і точка D – в ІV чверті

Якщо точка лежить на площинах проекцій, то одна її проекція обов’язково співпадає з даною точкою, а друга – лежить на осі проекцій. Одна із координат рівна нулю.

Таблиця 1.3 – Проекції точок, які лежать в площинах проекції

Необхідна умова	Наочне зображення	Епюр
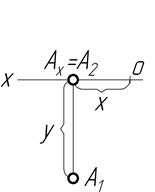
На передній полі p1 Z=0 Y>0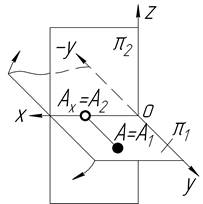
Продовження таблиці 1.3
Необхідна умова	Наочне зображення	Епюр
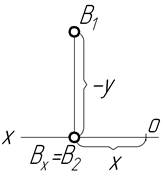
На задній полі p1 Z=0 Y<0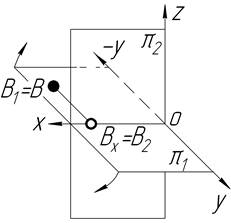
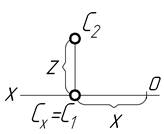
На верхній полі p2 Y=0 Z>0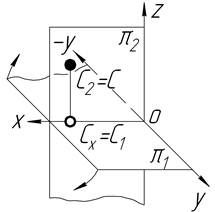
На нижній полі p2 Y=0 Z<0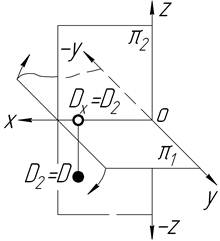
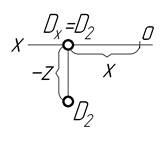
На осі OX Z=Y=0

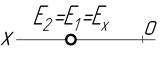
Наочні зображення і епюри точок, які лежать в площинах проекцій, показані в таблиці 1.3: точка А – в горизонтальній площині проекцій на її передній полі;

точка В – в горизонтальній площині проекцій на її задній полі;

точка С – у фронтальній площині проекцій на її верхній полі;

точка D – у фронтальній площині проекцій на її нижній полі;

точка Е – на осі проекцій (одночасно лежить на двох площинах проекцій, тому обидві проекції точки Е співпадають з даною точкою і дві координати рівні нулю.

1.2 Проекція точки на три площини проекцій

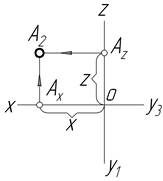
У таблиці 1.4 показано послідовну побудову проекцій точки за її координатами. Координати точки записуються завжди у визначеному порядку, із своїми знаками: А (х; y; z). Кожна проекція визначається своїми координатами. Координата — це відстань від точки до площин проекцій. Так, координати х та y визначають горизонтальну проекцію точки, координати х та z ─ фронтальну, а координати y та z — профільну проекцію точки.

Таблиця 1.4. ─ Координати проекцій точки

Координати	Наочне зображення	Епюр
X та Z	Фронтальна проекція точки
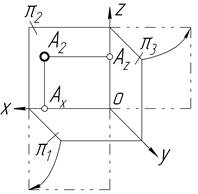
X та Y	Горизонтальна проекція точки
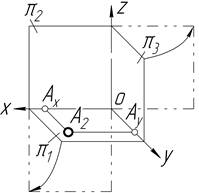
Z та Y	Профільна проекція точки

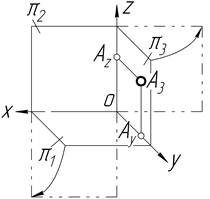
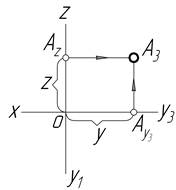
На рис. 1.4 зображено побудови наочного зображення та епюру точки за заданими координатами цієї точки: А (х; y; z).

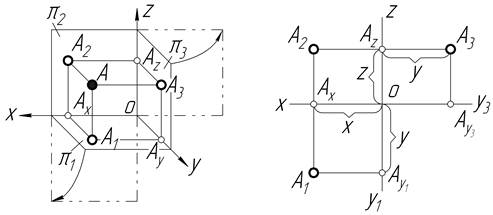
Рисунок 1.4 ─ Побудова наочного зображення та епюру точки А (х; y; z)

Так як всі три координати точки А додатні, то точка розміщена в І октанті.

Відрізки, які відповідають координатам точки, відкладаємо на відповідних координатних осях: ОАх на осі ОХ, ОАy на осі OY і ОАz на осі ОZ. Після цього через точки Ах, Аy, Аz, проводимо лінії проекційного зв’язку, на перетині яких маємо шукані проекції точки А.

Так само, маючи епюр точки, можна знайти її координати і тим самим визначити положення точки в просторі відносно площин проекцій.

1 Для комплексного креслення (рисунка) або епюра точки маємо такі положення:

2 Фронтальна та горизонтальна проекції точки завжди знаходяться на одній вертикальній лінії проекційного зв’язку (рис. 1.4).

3 Фронтальна та профільна проекції точки знаходяться на одній горизонтальній лінії проекційного зв’язку (рис. 1.4).

4 Віддаль від фронтальної проекції точки до осі OX визначає віддаль самої точки від горизонтальної площини проекцій П₁ (висоту), числова величина якої виражається координатою Z (рис. 1.4).

5 Віддаль від горизонтальної проекції точки до осі OX визначає величину віддалі самої точки до фронтальної площини проекцій π₂ (глибину) і виражається координатою Y (рис. 1.4).

6 Віддаль від профільної проекції точки до осі OZ дорівнює віддалі від горизонтальної проекції точки до осі OX або координаті Y (рис. 1.4).

7 За фронтальною та горизонтальною проекціями точки завжди можна визначити її профільну проекцію або графічною побудовою, або перенесенням величини координати Y з горизонтальної площини проекції на профільну (рис. 1.5).

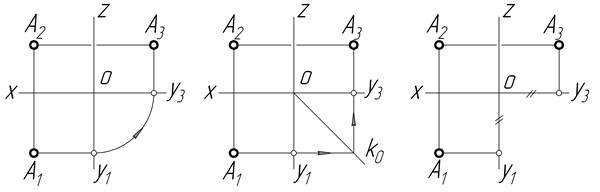
а) б) в)

Рисунок 1.5 ─ Побудова профільної проекції точки: а) проекційний спосіб;

б) за допомогою постійної прямої К₀; в) координатний спосіб

У таблиці 1.5 зведені приклади наочних зображень та епюри точок в октантах простору.

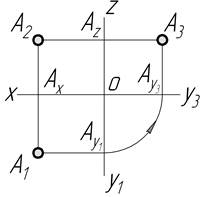
Таблиця 1.5 ─ Наочні зображення та епюри точок в октантах простору

Октант	Наочне зображення	Епюр
І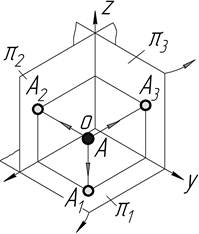
ІІ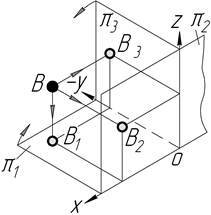
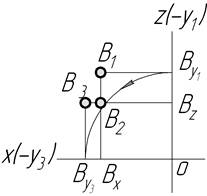
ІІІ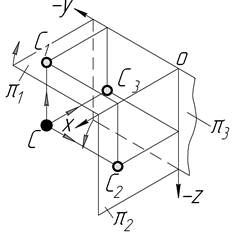
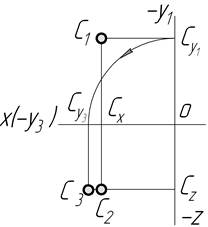
ІV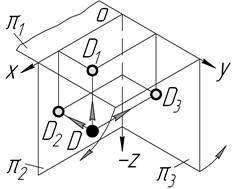
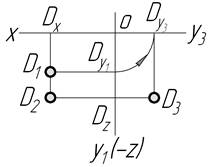
Продовження таблиці 1.5
Октант	Наочне зображення	Епюр
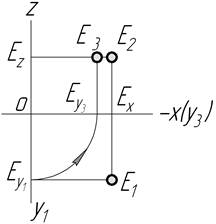
V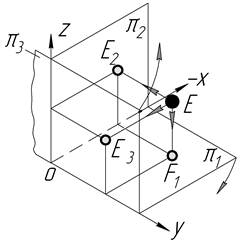
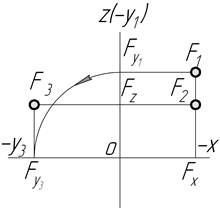
VІ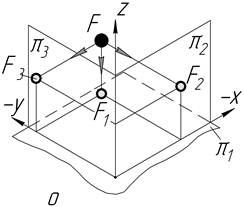
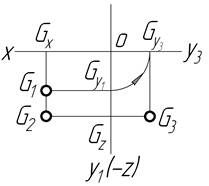
VІІ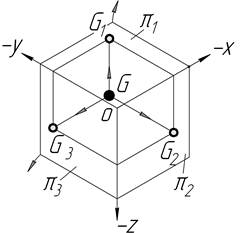
VІІІ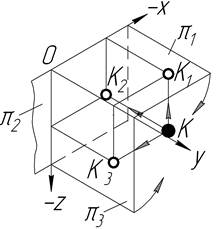

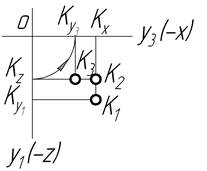
приклади розв’язку задач

Задача 1 Побудувати епюр та наочне зображення точок в системі двох площин проекцій: А(30,40,25), N(25,0,30), М(25,30,0)

Будь-яка точка простору може бути однозначно задана трьома координатами ─ x, y, z або скорочено А(x, y, z). За даними умови задачі для побудови комплексного креслення точки необхідно вздовж осі ОХ відкласти від початку координат число x, що дає точку А_х ─ проекцію точки А на осі ОХ. Далі через цю точку проводимо пряму лінію(лінію проекційного зв’язку), яка повинна бути перпендикулярною до осі ОХ. Відкладаючи на цій лінії координати y та z, отримаємо відповідно горизонтальну А₁ та фронтальну А₂ проекці точки А. Послідовність побудови епюру та наглядного зображення для точок А, N та M подано у таблиці 1.6.

Таблиця 1.6 ─ Розв’язок задачі 1

	Наочне зображення	Епюр
Точка А X=30 Y=40 Z=25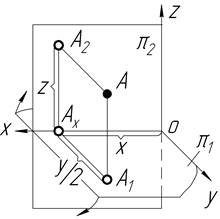
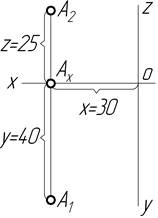
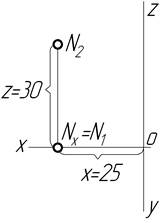
Точка N X=25 Y= 0 Z=30 на p2 верхній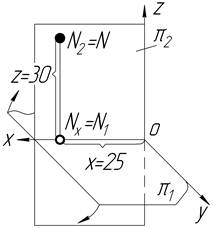
Точка М X=25 Y=30 Z= 0 на p2 передній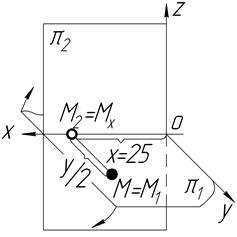

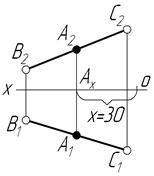
Задача 2 Побудувати наочне зображення та епюр точки В, яка симетрична точці А (25,30,15) відносно p₁ та точки С, яка симетрична точці А відносно p₂.

Згідно умови задачі координати точки А додатні, а отже, точка знаходиться у першій чверті. Точка В, яка буде симетрична точці А, матиме такі самі координати за абсолютною величиною, але координата Y змінить свій знак на протилежний. Отже, точка В знаходитьсяу другій чверті. Точка С, яка симетрична точці А відносно горизонтальної площини проекцій, розміщена у четвертій чверті, а отже, координата Z змінить свій знак на протилежний.

Розв’язок задачі представлений у таблиці 1.7.

Таблиця 1.7 ─ Розв’язок задачі 3

	Наочне зображення	Епюр
Точка А X=25 Y=30 Z=15 І чверть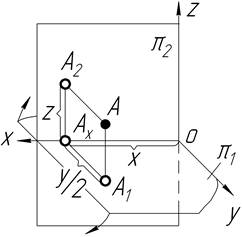
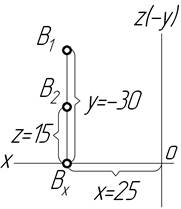
Точка В X=25 Y=-30 Z=15 ІІ чверть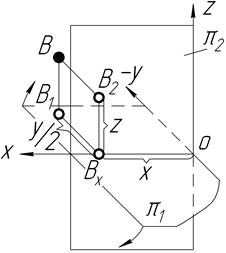
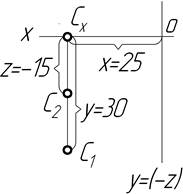
Точка С X=25 Y=30 Z=-15 ІV чверть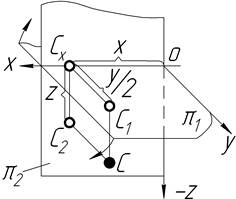

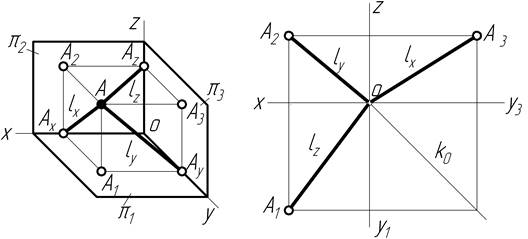
Задача 3 Вказати найкоротшу віддаль від точки А до координатних осей на наочному зображенні та комплексному рисунку (епюрі) (рис.1.6).

Відстань від точки А до координатних осей позначимо на епюрі і на ночному зображенні суцільною потовщеною лінією, де: l_x ─ віддальвід точки А до осі ОХ; l_y ─ віддаль від тоски А до осі ОY; l_z ─ віддаль від точки А до осі ОZ.

а) б) Рисунок 1.6  

ЗАПИТАННЯ ТА ЗАВДАННЯ ДЛЯ САМОПЕРЕВІРКИ

1 По якій осі перетинаються площини проекцій:

- горизонтальна і фронтальна?

- горизонтальна і профільна?

- фронтальна і профільна?

2 Яка координата визначає відстань від точки до:

- горизонтальної площини проекцій?

- фронтальної площини проекцій?

- профільної площини проекцій?

3 У якій площині проекцій розташовані точки, які мають такі координати:

- X≠0, Y≠0, Z=0

- X=0, Y≠ 0, Z≠0

- X=0, Y≠0, Z≠0

4 На якій осі проекцій розташовані точки, які мають такі координати:

- X≠0, Y=0, Z=0

- X=0, Y≠0, Z=0

- X=0, Y=0, Z≠0

5 Вкажіть місце розташування точок

А(20,30,40), В(0,30,0), С(10,-30,-20), D(40,-15,0), Е(50,0,-10)

6 Задані координати шести точок:

А (30,10,0), В(10,20,20), С(20,-10,30), D(40,0,20), E(30,50,10), F(20,0,0)

- Яка з точок розміщена у фронтальній площині проекцій?

- Яка з точок розміщена у горизонтальній площині проекцій?

- Яка з точок розміщена у другій чверті?

- Яка з точок розміщена у першій чверті?

- Яка з точок найбільше віддалена від фронтальної площини проекцій?

- Яка точка лежить на осі проекції ОХ.

7 Вказати місце розташування у просторі заданих на епюрі точок:

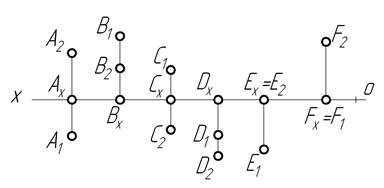
8 На рисунку задано епюри декількох точок. За комплексним рисунком визначити:

- Яка з точок розташована у третій чверті?

- Яка з точок розташована у другій чверті?

- Яка з точок рівновіддалена від двох площин проекцій?

- Яка з точок найбільше віддалена від горизонтальної площини проекцій?

- Яка з точок найближче знаходиться до горизонтальної площини проекцій?

- У якої з точок координата Z дорівнює нулю?

9 Яка з точок знаходиться найближче до осі проекцій OY?; а яка до OZ?

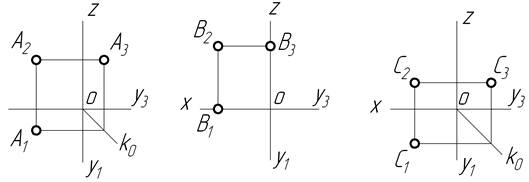
а) б) в)

10 Яка з точок найближче розташована до фронтальної площини проекцій?

а) А (35;-80;-40); в) С (25;30;-55);

б) В (15;5;5); г) D (15;15;-15)

11. Яка з точок належить горизонтальній площині проекцій?

а) А (0;50;10); в) С (10;-30;-30);

б) В (15;10;65); г) D (35;25;5)

1.3 Пряма лінія

Положення прямої у просторі визначається положенням її відносно площин проекцій. Спроектувати пряму лінію означає спроектувати дві її точки та з’єднати однойменні проекції точок між собою. Кожна пряма у просторі проектується на площину проекцій у вигляді прямої лінії або точки (якщо пряма перпендикулярна до площини проекцій). Пряма може лежати на будь-якій площині проекцій чи розміщуватись на одній із трьох осей проекцій.

Пряма у просторі визначається за двома точками,які лежать на цій прямій. Якщо у просторі точка лежить на прямій,то на епюрі проекції цієї точки лежать на однойменних проекціях прямої.

Прямою довільного положення називають пряму, яка не паралельна і не перпендикулярна до жодної з площин проекцій. Проекції такої прямої нахилені до усіх трьох осей проекцій.

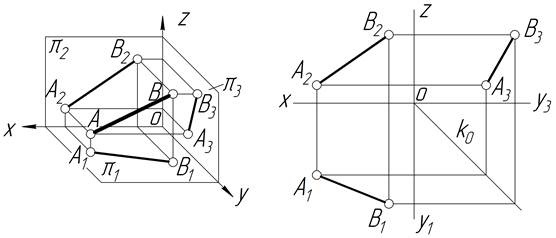
а) б)

Рисунок 1.7 –Зображення прямої загального положення

б)на комплексному рисунку; а) на наочному зображенні

Відрізок прямої довільного положення проектується на три площини проекцій у вигляді відрізків,які менші за сам відрізок і тим менші,чим більший кут нахилу відрізка до відповідної площини проекцій.Проекції відрізка довільного положення завжди менші ніж відрізок у просторі. Жодна з проекцій такого відрізка не паралельна і не перпендикулярна до осей проекцій.

Крім довільного,пряма може мати особливе положення. Пряма паралельна до однієї з площин проекцій ─ пряма рівня, пряма перпендикулярна до однієї з площин проекцій — пряма проекційна.

Особливі прямі, які паралельні до однієї з площин проекцій:

фронтальна – пряма, паралельна до площини π ₂;

горизонтальна – пряма, паралельна до площини π ₁;

профільна – пряма, паралельна до площини π ₃ .

Особливі прямі, які паралельні до двох площин проекцій і перпендикулярні до третьої площини проекцій:

фронтально-проекційна – пряма, перпендикулярна до площини π ₂ ;

горизонтально-проекційна –пряма, перпендикулярна до площини π ₁ ;

профільно-проекційна – пряма, перпендикулярна до площини π ₃

Для перших трьох прямих (про які згадано вище) характерним є те, що одна із проекцій відрізка, яким задана пряма, проектується в дійсну величину і саме на ту площину проекцій, до якої він паралельний.

Для наступних трьох прямих (про які згадано вище) характерним є те, що одна із проекцій відрізка, яким задана пряма, вироджується в точку і саме на ту площину проекцій, до якої він перпендикулярний.

Прямі особливого положення у просторі зведені у таблиці 1.8

Таблиця 1.8 ─ Прямі особливого положення

Умова	Наочне зображення	Епюр
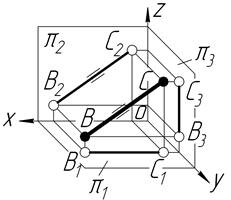
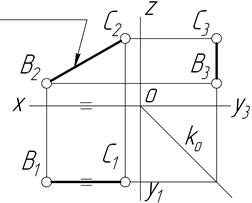
Const YC=YB	Фронтальний відрізок
Дійсна величина
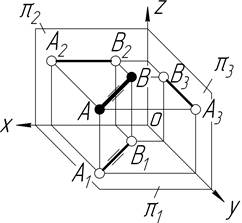
Const ZA=ZB	Горизонтальний відрізок
Дійсна величина
Const XC=XD	Профільний відрізок
Продовження таблиці 1.8
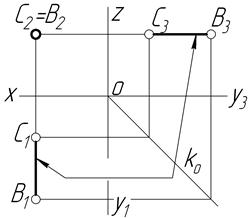
Const XВ=XC ZB=ZС	Фронтально-проекційний відрізок
	Дійсна величина
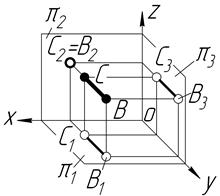
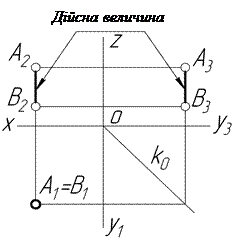
Const XА=XВ YА=YВ	Горизонтально-проекційний відрізок
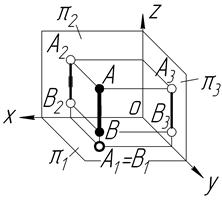
Const XD=XC YD=YС	Профільно-проекційний відрізок

Точка на прямій. Поділ відрізка прямої у заданому співвідношенні

Якщо точка лежить на прямій, то на епюрі проекції точки лежать на однойменних проекціях цієї прямої (рис.1.8).

Правильне також обернене твердження: якщо на епюрі проекції прямої проходять через однойменні проекції точки, то в просторі ця пряма проходить через точку (рис.1.8).

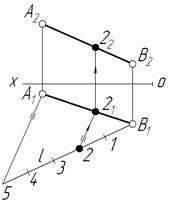Спираючись на властивості паралельного проектування щодо співвідношення відрізків прямої та їх проекцій, виявляємо, що для поділу відрізкапрямої в заданому пропорційному співвідношенні досить поділити у цьому співвідношенні одну з проекцій відрізка, а потім за допомогою ліній зв’язку перенести точки поділу на інші проекції відрізка (рис.1.9).

		Рисунок 1.9 - Поділ відрізка у співвідношенні 2:3

Рисунок 1.8 - Належність точки до прямої

Сліди прямої

Точка перетину прямої з відповідною площиною проекцій називаєтьсяслідом прямої.

Слід прямої ─ це точка,яка має одну координату рівну нулю,оскільки вона лежить на одній з площин проекцій.

Слід прямої ─ це границя переходу прямої з чверті в чверть і з октанту в октант.

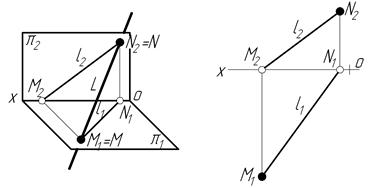
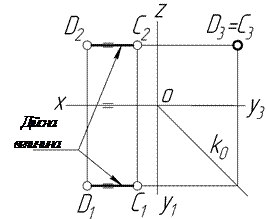
Рисунок 1.10 – Побудова слідів прямої l у системі трьох площин проекцій

Пряма загального положення в системі трьох площин проекцій має три сліди:

- перетин з горизонтальною площиною проекцій — горизонтальний слід;

- перетин з фронтальною площиною проекцій — фронтальний слід;

- перетин з профільною площиною проекцій — профільний слід.

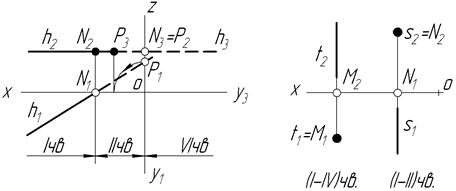
Прямі, які паралельні до однієї з площин проекцій, мають два сліди ─ сліду немає на площині, до якої пряма паралельна (рис. 1.11,а).

Прямі, перпендикулярні до однієї з площин проекцій, мають тільки один слід ─ до двох інших площин така пряма паралельна, тому перетин з ними відсутній (рис. 1.11,б).

	а) б) Рисунок 1.11 – Побудова слідів прямих особливого положення

Слід – це точка, яка лежить на прямій і в той же час належить площині проекцій. Тобтоце точка, яка має одну координату рівну нулю. Для фронтального сліду N, Y_N = 0, для горизонтального сліду М ─ Z_M = 0, а для профільного сліду Р ─ Х_Р = 0.

За положеннями слідів прямої на епюрі можна робити висновок про те, через які просторові кути проходить пряма і, яке положення вона займає в просторі.

Побудова дійсної величини відрізка прямої

Дата добавления: 2014-12-16