
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Электромагнетизм 1 страница
|
|
|
|
1. Связь магнитной индукции  с напряженностью
с напряженностью 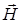 магнитного поля.
магнитного поля.
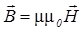 ,
,
где m - магнитная проницаемость однородной среды; m 0 - магнитная постоянная. В вакууме m = 1, и магнитная индукция в вакууме
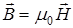 .
.
2. Закон Био-Савара-Лапласа
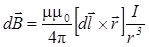 или
или 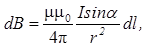
где 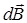 - магнитная индукция поля, создаваемого элементом провода длиной
- магнитная индукция поля, создаваемого элементом провода длиной 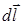 c током I;
c током I; 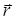 - радиус-вектор, направленный от элемента проводника к точке, в которой определяется магнитная индукция; a - угол между радиус-вектором и направлением тока в элементе провода.
- радиус-вектор, направленный от элемента проводника к точке, в которой определяется магнитная индукция; a - угол между радиус-вектором и направлением тока в элементе провода.
3. Принцип суперпозиции магнитных полей
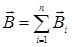 или
или 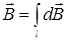
|
для 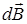 , созданных элементом тока
, созданных элементом тока 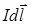 .
.
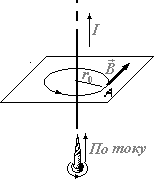
Направление вектора магнитной индукции 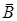 поля, создаваемого прямым током, определяется по правилу буравчика (правого винта). Для этого проводим магнитную силовую линию (штриховая линия на рис.) и по касательной к ней в интересующей нас точке проводим вектор
поля, создаваемого прямым током, определяется по правилу буравчика (правого винта). Для этого проводим магнитную силовую линию (штриховая линия на рис.) и по касательной к ней в интересующей нас точке проводим вектор 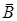 . Вектор магнитной индукции
. Вектор магнитной индукции 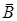 в точке А направлен перпендикулярно плоскости чертежа от нас.
в точке А направлен перпендикулярно плоскости чертежа от нас.
Рис. 1
4. Магнитная индукция в центре кругового тока
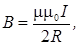
где R - радиус кругового витка.
Магнитная индукция на оси кругового тока
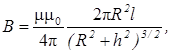
где h - расстояние от центра витка до точки, в которой определяется магнитная индукция.
Магнитная индукция поля, создаваемого отрезком провода с током (вывод этой формулы в примере № 1):
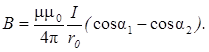
Магнитная индукция поля, создаваемого бесконечно длинным прямолинейным проводником с током:
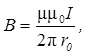
где r 0 - расстояние от оси провода до точки, в которой определяется магнитная индукция.
Магнитная индукция поля бесконечно длинного соленоида
B = mm0 nI,
где n - отношение числа витков соленоида N к его длине l.
5. Сила, действующая на элемент провода с током в магнитном поле (закон Ампера):
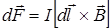 ,
,
где 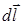 - вектор, равный по модулю длине участка провода и совпадающий по направлению с током; a - угол между направлением тока в проводе и вектором магнитной индукции
- вектор, равный по модулю длине участка провода и совпадающий по направлению с током; a - угол между направлением тока в проводе и вектором магнитной индукции  .
.
Для однородного магнитного поля и прямого отрезка провода получим:
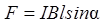 .
.
6. Магнитный момент плоского контура с током
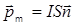 ,
,
где 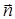 - единичный вектор нормали (положительной) к плоскости контура; I - сила тока, протекающего по контуру; S - площадь контура.
- единичный вектор нормали (положительной) к плоскости контура; I - сила тока, протекающего по контуру; S - площадь контура.
7. Механический вращающий момент, действующий на контур с током, помещенный в однородное магнитное поле:
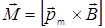 или
или 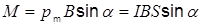 ,
,
где a - угол между векторами 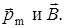
8. Сила Лоренца
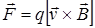 или
или 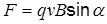 ,
,
где 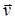 - скорость заряженной частицы; a - угол между векторами
- скорость заряженной частицы; a - угол между векторами 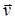 и
и  .
.
Если частица находится одновременно в электрическом и магнитном полях, то на нее действует сила
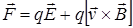 .
.
9. Магнитный поток (через поверхность S):
а) в случае однородного магнитного поля и плоской поверхности
Ф = BS cos a или Ф = B n S,
где S - площадь контура; a - угол между нормалью к плоскости контура и вектором магнитной индукции;
б) в случае неоднородного поля и произвольной поверхности
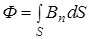
(интегрирование ведется по всей поверхности).
Потокосцепление (полный поток) – Y = NФ.
Эта формула верна для соленоида и тороида с равномерной намоткой плотно прилегающих друг к другу N витков.
10. Работа по перемещению замкнутого контура с током в магнитном поле dA=I dФ или А=I×DФ.
11. Основной закон электромагнитной индукции (закон Фарадея-Максвелла): 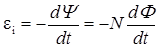 .
.
Разность потенциалов на концах проводника, движущегося со скоростью 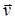 в магнитном поле, U = Blv· sin a,
в магнитном поле, U = Blv· sin a,
где l - длина провода; a - угол между векторами 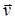 и
и  .
.
Заряд, протекающий по замкнутому контуру при изменении магнитного потока, пронизывающего этот контур: 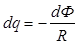 или
или 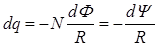 , где R - сопротивление контура.
, где R - сопротивление контура.
12. Индуктивность контура L = Ф / I.
Индуктивность соленоида L = mm0 n 2 lS,
где n - отношение числа витков соленоида к его длине; l – длина соленоида, S – площадь его поперечного сечения.
13. Э.д.с. самоиндукции
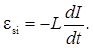
14. Мгновенное значение силы тока в цепи, обладающей сопротивлением R и индуктивностью L:
а) 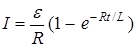 - при замыкании цепи, где e -э.д.с. источника тока; t - время, прошедшее после замыкания цепи;
- при замыкании цепи, где e -э.д.с. источника тока; t - время, прошедшее после замыкания цепи;
б) 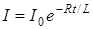 - при размыкании цепи, где I 0 - сила тока в цепи при t = 0; t - время, прошедшее с момента размыкания цепи.
- при размыкании цепи, где I 0 - сила тока в цепи при t = 0; t - время, прошедшее с момента размыкания цепи.
15. Энергия магнитного поля соленоида W = 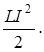
Объемная плотность энергии магнитного поля (отношение энергии поля к его объему)
w = BH /2 = B 2/(2mm0) = mm0 H 2/2.
4.1. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
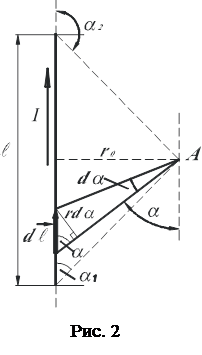
№ 1. По отрезку прямого провода длиной l = 80 см течет ток I = 50 А. Определить магнитную индукцию  поля, создаваемого этим током в точке А, равноудаленной от концов отрезка провода и находящейся на расстоянии r 0 = 30 см от его середины.
поля, создаваемого этим током в точке А, равноудаленной от концов отрезка провода и находящейся на расстоянии r 0 = 30 см от его середины.
Р е ш е н и е.
Для решения задачи воспользуемся законом Био-Савара-Лапласа
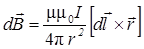 (1)
(1)
и принципом суперпозиции магнитных полей:
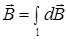 , (2)
, (2)
где символ l означает, что интегрирование распространяется на всю длину провода, 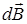 магнитная индукция, создаваемая элементом тока
магнитная индукция, создаваемая элементом тока 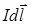 в точке, определяемой радиус-вектором
в точке, определяемой радиус-вектором 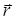 ; m 0 - магнитная постоянная; m - магнитная проницаемость среды, в которой находится провод (в нашем случае m = 1). Векторы
; m 0 - магнитная постоянная; m - магнитная проницаемость среды, в которой находится провод (в нашем случае m = 1). Векторы 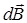 от различных элементов тока сонаправлены, поэтому выражения (1), (2) можно переписать в скалярной форме:
от различных элементов тока сонаправлены, поэтому выражения (1), (2) можно переписать в скалярной форме:
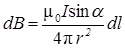 ,
, 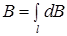 ,
,
где a есть угол между вектором 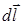 и радиус-вектором
и радиус-вектором 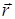 . Таким образом,
. Таким образом,
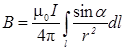 . (3)
. (3)
Выразим длину элемента провода dl через угол d a: dl = rd a/sina.
Запишем выражение 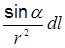 в виде
в виде 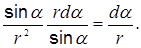 Переменная r также зависит от a (r = r 0/sina), следовательно:
Переменная r также зависит от a (r = r 0/sina), следовательно: 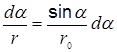 . Таким образом, выражение (2) можно переписать в виде
. Таким образом, выражение (2) можно переписать в виде 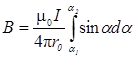 , где a1 и a2 - пределы интегрирования.
, где a1 и a2 - пределы интегрирования.
Выполним интегрирование:
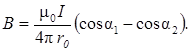 (4)
(4)
При симметричном расположении точки А относительно отрезка провода cos a2 = -cos a1. С учетом этого формула (4) примет вид
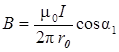 . (5)
. (5)
Из рис.2 следует
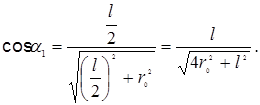
Подставив выражение cosa1 в формулу (5), получим
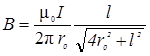 . (6)
. (6)
Произведя вычисления по формуле (6), получим В = 26,7 мкТл.
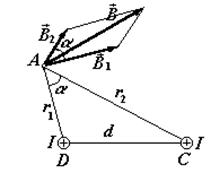
№ 2. Два бесконечно длинных провода D и С, по которым текут в одном направлении токи силой I = 60 А, расположены на расстоянии d = 10 см друг от друга. Определить магнитную индукцию  поля, создаваемого проводниками в точке А. (см. рис.), отстоящей от оси одного проводника на расстояние r 1 = 5 см, от другого на r 2 = 12 см.
поля, создаваемого проводниками в точке А. (см. рис.), отстоящей от оси одного проводника на расстояние r 1 = 5 см, от другого на r 2 = 12 см.
|
Р е ш е н и е.
Для нахождения магнитной индукции  в точке А воспользуемся принципом суперпозиции магнитных полей:
в точке А воспользуемся принципом суперпозиции магнитных полей:  =
=  1+
1+  2.
2.
Модуль вектора  может быть найден из теоремы косинусов
может быть найден из теоремы косинусов
Рис. 3
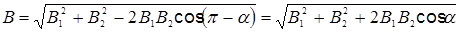 , (1)
, (1)
где a - угол между векторами  1 и
1 и  2.
2.
Магнитные индукции  1 и
1 и  2 выражаются соответственно через силу тока I и расстояния r 1 и r 2 от проводов до точки А
2 выражаются соответственно через силу тока I и расстояния r 1 и r 2 от проводов до точки А
В 1 = m0 I /(2p r 1); B 2 = m0 I /(2p r 2).
Подставляя выражения В 1 и В 2 в формулу (1), получаем
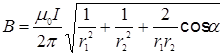 . (2)
. (2)
Вычислим cos a по теореме косинусов (Ð a = Ð DAC как углы с соответственно перпендикулярными сторонами), d2 = r 12 + r 22 - 2 r 1 r2 cos a,
где d - расстояние между проводами. Отсюда
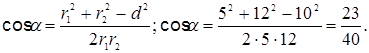
Подставим в формулу (2) числовые значения физических величин и произведем вычисления:
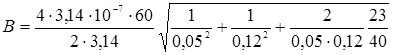 = 308 мкТл.
= 308 мкТл.
№ 3. По тонкому проводящему кольцу радиусом R = 10 см течет ток I = 80 А. Найти магнитную индукцию  в точке А, равноудаленной от всех точек кольца на расстояние r = 20 см.
в точке А, равноудаленной от всех точек кольца на расстояние r = 20 см.
Р е ш е н и е.
Для решения задачи воспользуемся законом Био-Савара-Лапласа:
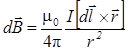 ,
,
где d  - магнитная индукция поля, создаваемого элементом тока I
- магнитная индукция поля, создаваемого элементом тока I 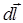 в точке, определяемой радиус-вектором
в точке, определяемой радиус-вектором 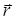 .
.
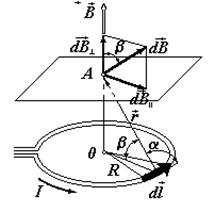
Выделим на кольце элемент 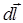 и от него в точку А проведем радиус-вектор
и от него в точку А проведем радиус-вектор 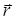 (рис. 4). Вектор d
(рис. 4). Вектор d  направим в соответствии с правилом буравчика.
направим в соответствии с правилом буравчика.
|
Согласно принципу суперпозиции магнитных полей, магнитная индукция  в точке А определяется интегрированием:
в точке А определяется интегрированием: 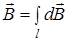 , где интегрирование ведется по всем элементам dl кольца.
, где интегрирование ведется по всем элементам dl кольца.
Разложим вектор d  на две составляющие: перпендикулярную плоскости
на две составляющие: перпендикулярную плоскости
кольца d  ^ и параллельную d
^ и параллельную d  ||, т.е.
||, т.е. 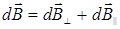 .Тогда
.Тогда 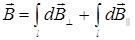 ,
,
Рис. 4
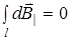 из соображений симметрии, а векторы
из соображений симметрии, а векторы 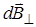 от различных элементов dl сонаправлены, следовательно
от различных элементов dl сонаправлены, следовательно 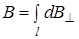 , где dB ^ = dB cos b и dB =
, где dB ^ = dB cos b и dB = 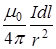 (поскольку
(поскольку 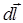 перпендикулярен
перпендикулярен 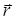 , то sin a = 1). Таким образом,
, то sin a = 1). Таким образом, 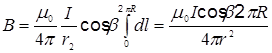 , где cosb = R / r (см. рис 4). Окончательно получим:
, где cosb = R / r (см. рис 4). Окончательно получим: 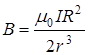 .
.
Выразим все величины в единицах СИ и произведем вычисления:
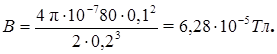
Вектор  направлен по оси кольца в соответствии с правилом буравчика.
направлен по оси кольца в соответствии с правилом буравчика.
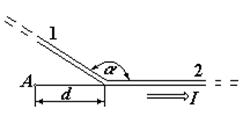
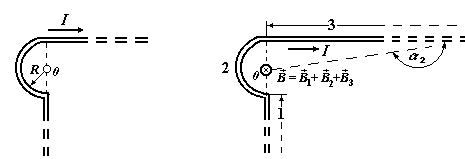
№ 4. Длинный провод с током I = 50 А изогнут под углом a = (2/3)p.. Определить магнитную индукцию  в точке А (см. рис. 5). Расстояние d = 5 см.
в точке А (см. рис. 5). Расстояние d = 5 см.
|
|
Рис. 5
Рис. 5
Р е ш е н и е.
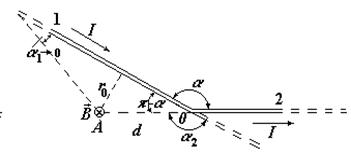
Изогнутый провод можно рассматривать как два длинных провода, концы которых соединены в точке О (Рис. 5) В соответствии с принципом суперпозиции магнитных полей магнитная индукция  в точке А будет равна геометрической сумме индукций
в точке А будет равна геометрической сумме индукций  1 и
1 и  2 магнитных полей, создаваемых отрезками длинных проводов 1 и 2, т.е.
2 магнитных полей, создаваемых отрезками длинных проводов 1 и 2, т.е.  =
=  1 +
1 +  2.
2.
Магнитная индукция  2 равна нулю. Это следует из закона Био-Савара-Лапласа, согласно которому в точках, лежащих на оси провода, d
2 равна нулю. Это следует из закона Био-Савара-Лапласа, согласно которому в точках, лежащих на оси провода, d  = 0, т.к. [ d
= 0, т.к. [ d 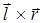 ]= 0.
]= 0.
Магнитную индукцию B 1 найдем, воспользовавшись соотношением (4), из примера 1: 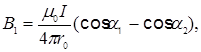 где r 0 - кратчайшее расстояние от провода 1 до точки А (см. рис. 5)
где r 0 - кратчайшее расстояние от провода 1 до точки А (см. рис. 5)
В нашем случае a 1®0 (провод длинный), a 2 = a = 2 p /3. Расстояние r 0 = d sin(p - a). Тогда магнитная индукция 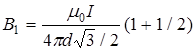 .
.
Так как B =B 1 (B 2 = 0), то 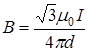 .
.
Вектор 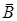 сонаправлен с вектором
сонаправлен с вектором 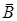 1 и направление его определяется правилом правого винта. На рис. 5 это направление отмечено крестиком в кружочке (перпендикулярно плоскости чертежа, от нас).
1 и направление его определяется правилом правого винта. На рис. 5 это направление отмечено крестиком в кружочке (перпендикулярно плоскости чертежа, от нас).
Произведем вычисления:
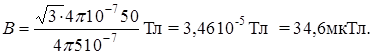
№ 5. Два бесконечно длинных провода скрещены под прямым углом (см. рис. 6) По проводам текут токи I 1 = 80 A и I 2 = 60 A. Расстояние d между проводами равно 10 см. Определить магнитную индукцию 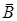 в точке А, одинаково удаленной от обоих проводов.
в точке А, одинаково удаленной от обоих проводов.
Р е ш е н и е.
В соответствии с принципом суперпозиции магнитных полей индукция 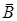 магнитного поля, создаваемого токами I 1 и I 2, определяется
магнитного поля, создаваемого токами I 1 и I 2, определяется
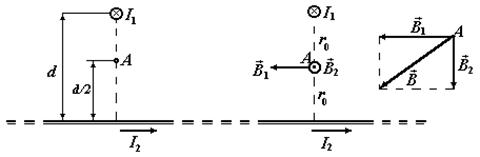
Рис. 6
выражением  =
=  1 +
1 +  2, где
2, где  1 - индукция магнитного поля, созданного в точке А током I 1;
1 - индукция магнитного поля, созданного в точке А током I 1;  2 - индукция магнитного поля, созданного в точке А током I 2 (направление отмечено точкой в кружочке - перпендикулярно плоскости чертежа к нам).
2 - индукция магнитного поля, созданного в точке А током I 2 (направление отмечено точкой в кружочке - перпендикулярно плоскости чертежа к нам).
Векторы  1 и
1 и  2, взаимно перпендикулярны, их направления находятся по правилу буравчика, и изображены в двух проекциях на рисунке. Модуль
2, взаимно перпендикулярны, их направления находятся по правилу буравчика, и изображены в двух проекциях на рисунке. Модуль  можно определить по теореме Пифагора (см. рис. 6)
можно определить по теореме Пифагора (см. рис. 6)
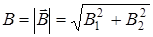 ,
,
В 1 и В 2 определяются по формулам расчета магнитной индукции для бесконечно длинного прямолинейного провода с током:
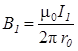 и
и 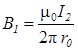 .
.
В нашем случае r 0 = d /2. Тогда 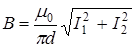 .
.
Произведем вычисления: 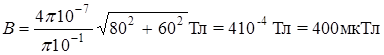 .
.
 № 6. Бесконечно длинный провод изогнут так, как изображено на рис.7. Радиус R дуги окружности равен 10 см. Определить индукцию
№ 6. Бесконечно длинный провод изогнут так, как изображено на рис.7. Радиус R дуги окружности равен 10 см. Определить индукцию  магнитного поля, создаваемого в точке О током I = 80 А, текущим по этому проводу.
магнитного поля, создаваемого в точке О током I = 80 А, текущим по этому проводу.
Р е ш е н и е.
Магнитную индукцию  в точке О найдем, используя принцип суперпозиции магнитных полей:
в точке О найдем, используя принцип суперпозиции магнитных полей: 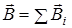 .
.
|
Рис. 7
В нашем случае провод можно разбить на три части (см. рис 7): два прямолинейных провода (1 и 3), одним концом уходящие в бесконечность, и дугу полуокружности (2) радиуса R. Тогда 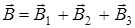 , где
, где 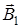 ,
, 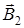 и
и 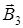 - индукции магнитных полей в точке О, создаваемые током первого, второго и третьего участков провода.
- индукции магнитных полей в точке О, создаваемые током первого, второго и третьего участков провода.
Так как точка О лежит на оси провода 1, то 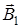 = 0 и тогда
= 0 и тогда  =
= 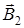 +
+ 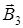 . Учитывая, что векторы
. Учитывая, что векторы 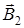 и
и 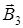 направлены в соответствии с правилом буравчика перпендикулярно плоскости чертежа от нас, геометрическое суммирование можно заменить алгебраическим: В = В 2 + В 3.
направлены в соответствии с правилом буравчика перпендикулярно плоскости чертежа от нас, геометрическое суммирование можно заменить алгебраическим: В = В 2 + В 3.
Магнитную индукцию В 2 найдем, воспользовавшись выражением для магнитной индукции в центре кругового тока: 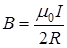 .
.
В нашем случае магнитное поле в точке О создается лишь половиной кругового тока, поэтому 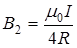 .
.
Магнитную индукцию В 3 найдем, применив соотношение (4), пример 1: 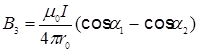 .
.
В нашем случае r 0 = R, a1 = p/2 (cos a1 = 0), a 2 ®p (cos a2 = -1). Тогда 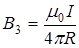 .
.
Используя найденные выражения, получим В = В 2 + В 3 = 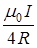 +
+ 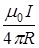 ,
,
ли 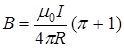 .
.
Произведем вычисления:
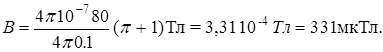
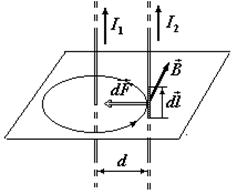
№ 7. По двум параллельным прямым проводам длиной l = 2 м каждый, находящихся на расстоянии d = 20 см друг от друга, текут одинаковые токи I = 1 кА. Вычислить силу взаимодействия токов.
Р е ш е н и е.
Взаимодействие двух проводов, по которым текут токи, осуществляется через магнитное поле. Каждый ток создает магнитное поле, которое действует на другой провод.
Предположим, что оба тока (обозначим их I 1 и I 2) текут в одном направлении. Ток I 1 создает в месте расположения второго провода (с током I 2) магнитное поле, направление вектора магнитной индукции 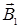 определяется по правилу буравчика. Модуль магнитной индукции В 1 задается соотношением
определяется по правилу буравчика. Модуль магнитной индукции В 1 задается соотношением
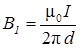 . (1)
. (1)
Согласно закону Ампера, на каждый элемент 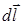 второго провода действует в магнитном поле сила
второго провода действует в магнитном поле сила 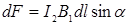 . Так как вектор
. Так как вектор 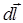 перпендикулярен вектору
перпендикулярен вектору  , то
, то 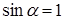 и тогда dF = I 2 B 1 dl. Подставив в это выражение значение В 1, получим
и тогда dF = I 2 B 1 dl. Подставив в это выражение значение В 1, получим 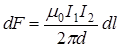 .
.
|
Силу F взаимодействия токов найдем интегрированием:
|
|
|
|
|
Дата добавления: 2014-12-16; Просмотров: 755; Нарушение авторских прав?; Мы поможем в написании вашей работы!