Электромагнетизм 2 страница

.

Учитывая, что I ₁= I ₂ = I, получим

.

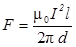Произведем вычисления:

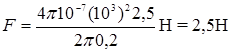
Рис. 8

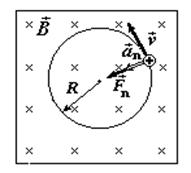
Сила 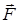сонаправлена с силой d 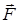, а направление d 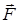определяется правилом левой руки.

№ 8. Протон, прошедший ускоряющую разность потенциалов U = 600 В, влетел в однородное магнитное поле с индукцией В = 0,3 Тл и начал двигаться по окружности. Вычислить радиус R окружности.

Р е ш е н и е.

Движение заряженной частицы в одно­родном магнитном поле будет происходить по окружности только в том случае, если частица влетит в магнитное поле перпендикулярно линиям индукции: 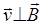. Так как сила Лоренца перпендикулярна вектору 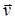, то она сообщает Рис. 9

частице (протону) нормальное ускорение 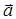_n.

Согласно второму закону Ньютона,

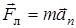, (1)

где m - масса протона. На рис. 9 совмещена траектория протона с плоскостью чертежа и дано (произвольно) направление вектора скорости 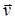. Силу Лоренца направим перпендикулярно вектору 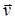к центру окружности (векторы 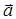_n и 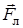сонаправлены.). Используя правило левой руки, определим направление магнитных силовых линий (направление вектора ).

Перепишем выражение (1) в скалярной форме (в проекции на радиус):

F _л = ma _n. (2)

В скалярной форме F _л = qvB sin a. В нашем случае 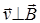и sin a = 1, тогда F _л = qvB. Так как нормальное ускорение a _n = v ²/ R, то выражение (2) перепишем следующим образом: qvB = m v ²/ R. Отсюда выразим радиус окружности:

R = mv / (qB). (3)

Скорость протона найдем, воспользовавшись связью между работой сил электрического поля и изменением кинетической энергии протона, т.е. А = D W, или q (j ₁ - j ₂) = W ₂ - W ₁, где (j₁ - j₂) = U - ускоряющая разность потенциалов (или ускоряющее напряжение); W ₁ и W ₂ - начальная и конечная кинетические энергии протона.

Пренебрегая начальной кинетической энергией протона W ₁» 0, и, учитывая, что W _к = mv ²/2, получим qU = mv ²/2.

Найдем из этого выражения скорость 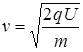и подставим ее в формулу (3), в результате получим

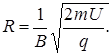(4)

Произведем вычисления: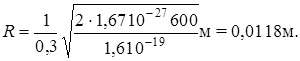

№ 9. Электрон, влетев в однородное магнитное поле(В = 0,2 Тл), стал двигаться по окружности радиуса R = 5 см. Определить магнитный момент р _m эквивалентного кругового тока.

Р е ш е н и е.

Электрон начинает двигаться по окружности, если он влетает в однородное магнитное поле перпендикулярно линиям магнитной индукции.

Движение электрона по окружности эквивалентно току, который в данном случае определяется выражением: 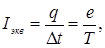где е - заряд электрона; Т - период его обращения.

Период обращения можно найти через скорость электрона и путь, проходимый электроном за период Т = (2 pR)/ v. Тогда

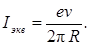(1)

По определению, магнитный момент контура с током выражается соотношением

P _m = I _эквS, (2)

где S - площадь, ограниченная окружностью, описываемой электроном S = pR ². Учитывая (1), (2) и (3), получим Р _m = 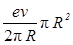или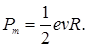

Известно, что R = mv/(еB) (см. пример 8). Тогда для скорости v электрона находим 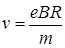. Подставив это выражение в (4) для магнитного момента P_m электрона получим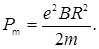

Произведем вычисления:

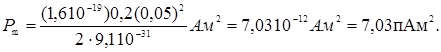
№ 10. Электрон движется в однородном магнитном поле по винтовой линии, радиус R которой равен 1 см и шаг h = 6 см. Определить период Т обращения электрона и его скорость v.

Р е ш е н и е.

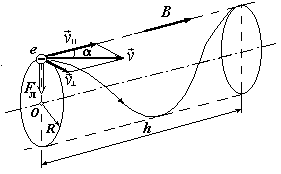
Электрон будет двигаться по винтовой линии, если он влетает в однородное магнитное поле под некоторым углом (a ¹ p/2) к линиям магнитной индукции. Разложим, как это показано на рис. скорость 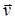электрона на две составляющие: параллельную

Рис. 10 вектору индукции 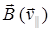и перпендикулярную ему (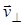). Скорость 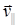в магнитном поле не изменяется и обеспечивает перемещение электрона вдоль силовых линий. Скорость 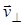в результате действия силы Лоренца будет изменяться только по направлению 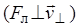(в отсутствие параллельной составляющей скорости движение электрона происходило бы по окружности в плоскости, перпендикулярной магнитным силовым линиям). Таким образом, электрон будет участвовать одновременно в двух движениях: равномерном со скоростью 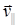и равномерном движении по окружности со скоростью .

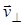Период обращения электрона связан с перпендикулярной составляющей скорости соотношением

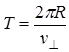. (1)

Найдем отношение R / v _^. Сила Лоренца сообщает электрону нормальное ускорение a _n = v ²/ R. Согласно второму закону Ньютона F _л = ma _n или

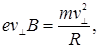(2)

где v _^ = v·sina. Получим соотношение R / v _^ = m / eB и подставим его в формулу (1);

(3)

Произведем вычисления: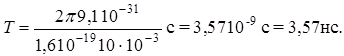

Модуль скорости v определяем через v _|| и v _^: .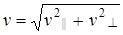

Из формулы (2) выразим перпендикулярную составляющую скорости: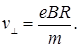

Параллельную составляющую скорости v _|| найдем из следующих соображений. За время, равное периоду обращения Т, электрон пройдет вдоль силовой линии расстояние, равное шагу винтовой линии, т.е. h = Tv _||, откуда v _|| = h / T. Подставив вместо Т правую часть выражения (3), получим

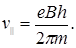
Таким образом, модуль скорости электрона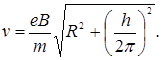

Произведем вычисления:

№ 11. Альфа-частица прошла ускоряющую разность потенциалов U = 104 В и влетела в скрещенные под прямым углом электрическое (Е = 10 кВ/м) и магнитное (В = 0,1 Тл) поля. Найти отношение заряда q a - частицы к ее массе m, если, двигаясь перпендикулярно обоим полям, частица не испытывает отклонений от прямолинейной траектории.

Р е ш е н и е.

Для того, чтобы найти отношение заряда q a - частицы к ее массе m, воспользуемся связью между работой сил электрического поля и изменением кинетической энергии частицы: qU = mv²/2, откуда

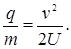(1)

Скорость v альфа-частицы определим из следующих соображений. В скрещенных электрическом и магнитном полях на движущуюся частицу действуют две силы: сила Лоренца F _л = q 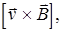направленная перпендикулярно скорости 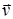и вектору магнитной индукции ; кулоновская сила F _к = qE, сонаправленная с вектором напряженности 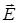электростатического поля.

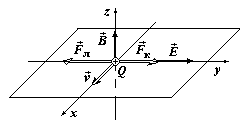
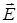Направим вектор магнитной индукции вдоль оси Оz, а вектор вдоль оси Oy (см. рис.), скорость 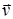- в положительном направлении оси Ох, тогда силы и 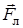будут направлены так, как показано на рис. 11.

Рис. 11 Альфа-частица не будет испытывать отклонения, если геометрическая сумма сил Кулона и Лоренца будет равна нулю + 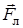= 0. В проекции на ось Оу получим равенство (при этом 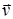^ и sin a = 1): qE - qvB = 0, откуда

v = E / B (2)

Подставив (2) в формулу (1), получим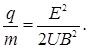

Произведем вычисления: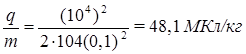

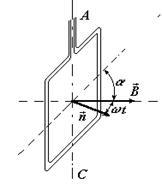
№ 12. Короткая катушка, содержащая N = 10³ витков, равномерно вращается с частотой n = 10 с^-1 относительно оси АС, лежащей в плоскости катушки и перпендикулярной линиям индукции однородного магнитного поля (В = 0,04 Тл). Определить мгновенное значение э.д.с. индукции e для тех моментов времени, когда плоскость катушки составляет угол a = 60⁰ с линиями поля. Площадь S катушки равна 100 см².

Р е ш е н и е.

Мгновенное значение э.д.с. индукции e_i определяется законом Фарадея

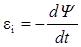. (1)

Потокосцепление Y = NФ, где N - число витков катушки, пронизываемых магнитным потоком Ф. Подставив это выражение в формулу (1), получим

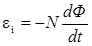. (2)

При вращении катушки магнитный поток Ф, пронизывающий катушку, изменяется по закону Ф =BS· cosj = BS· cos wt, где В - магнитная индукция; S - площадь катушки; j - угол между 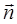и 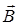; w - угловая скорость вращения.

Подставив в формулу (2) выражение магнитного потока Ф и, продифференцировав по

Рис. 12 времени, найдем мгновенное значение э.д.с. индук­ции: e_i = ωNBS· sinw t.

Учитывая, что угловая скорость вращения w катушки связана с частотой вращения n соотношением w = 2p n и что угол w t = p/2 - a (см. рис.), sin (p/2 - a) = cosa, получим e_i = 2p nNBS· cos a.

Произведем вычисления: e_i = 2×3,14×10×10³×0,04×10^-2×0,5 = 25,1 В.

№ 13. Квадратная проволочная рамка со стороной а = 5 см и сопротивлением R = 10 мОм находится в однородном магнитном поле (В = 40 мТл). Нормаль к плоскости рамки составляет угол a = 30⁰ с линиями магнитной индукции. Определить заряд q, который пройдет по рамке, если магнитное поле выключить.

Р е ш е н и е.

При выключении магнитного поля произойдет изменение магнитного потока. Вследствие этого в рамке возникнет э.д.с. индукции 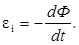Возникшая э.д.с. индукции вызовет в рамке индукционный ток, мгновенное значение которого можно определить по закону Ома для полной цепи I _i = e_i/ R, где R - сопротивление рамки. Тогда .

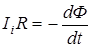Так как мгновенное значение силы индукционного тока I _i = dq / dt, то предыдущее выражение можно переписать в виде ,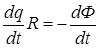

откуда

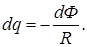(1)

Проинтегрировав выражение (1), найдем 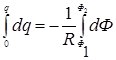или .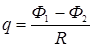

При выключенном поле Ф ₂ = 0, и последнее равенство перепишется в виде q = Ф ₁/ R. (2)

По определению магнитного потока Ф ₁ = BS· cosa. В нашем случае площадь рамки S = а ². Тогда

Ф ₁ = Ва ²cosa. (3)

Подставив (3) в (2), получим .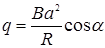

Произведем вычисления: .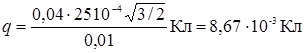

№ 14. Плоский квадратный контур со стороной а = 10 см, по которому течет ток I = 100 А, свободно установился в однородном магнитном поле (В = 1 Тл). Определить работу А, совершаемую внешними силами при повороте контура относительно оси, проходящей через середину его противоположных сторон, на угол j = 90⁰. При повороте контура сила тока в нем поддерживается неизменной.

Р е ш е н и е.

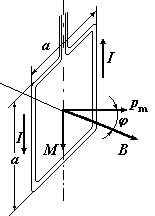
На контур с током в магнитном поле действует момент силы (см. рис. 13)

M = p _m B sin j, (1)

где p _m = IS= Ia ² - магнитный момент контура; В - индукция магнитного поля; j - угол между векторами 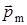(направлен по нормали к контуру) и .

По условию задачи в начальном положении контур свободно установился в магнитном поле. При этом момент силы равен нулю (М = 0), а значит, угол j = 0, т. е. векторы 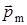и сонаправлены. Если внешние силы выведут контур из положения равновесия, то возникший момент сил будет стремиться возвратить контур в исходное положение. Против этого момента и будет совершаться работа внешними силами. Так как момент сил переменный (зависит от угла поворота j), то для подсчета работы применим

Рис. 13 формулу работы в дифференциальной форме dA = Mdj. Учитывая формулу (1), получаем dA = IBa ²sinj d j.

Взяв интеграл от этого выражения, найдем работу при повороте на конечный угол . Работа при повороте на угол j = 90⁰

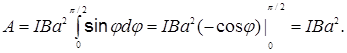(2)

Произведем вычисления: А = 100× 1 (0,1)² = 1 Дж.

Задачу можно решить другим способом.

Работа внешних сил по перемещению контура с током в магнитном поле равна произведению силы тока в контуре на изменение магнитного потока, пронизывающего контур: А = -IDФ = I(Ф ₁ - Ф ₂), где Ф ₁ - магнитный поток до перемещения, Ф ₂ - после. Ф ₁ = BS cos0⁰ = BS; Ф ₂ = BS cos90⁰ = 0. Следовательно, А = IBS = IBa ², что совпадает с формулой (2).

№ 15. На железный стержень длиной 50 см и сечением 2 см² намотан в один слой провод так, что на каждый сантиметр длины стержня приходится 20 витков. Определить энергию магнитного поля в сердечнике соленоида, если сила тока в обмотке 0,5 А.

Р е ш е н и е.

Энергия магнитного поля соленоида с индуктивностью L, по обмотке которого течет ток I, выражается формулой:

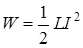. (1)

Индуктивность соленоида зависит от числа витков на единицу длины n, от объема сердечника V и от магнитной проницаемости m сердечника, т.е. L = mm ₀ n ² V, где m ₀ = магнитная постоянная.

Магнитную проницаемость можно выразить следующей формулой: 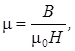где В - индукция магнитного поля, Н - напряженность.

Подставив в формулу (1) выражение индуктивности L и магнитной проницаемости, получим .

Объем сердечника выразим через длину l и сечение S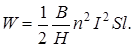

Напряженность магнитного поля найдем по формуле: Н = nI.

Подставив данные в единицах СИ, получим: Н = 2×10³× 0,5 А/м = 10³ А/м.

Значению напряженности намагничивающего поля в 10³ А/м в железе соответствует индукция В = 1,3 Тл (см. график зависимости между Н и В в приложении).

Произведем вычисления:

№ 16. Обмотка соленоида состоит из одного слоя плотно прилегающих друг к другу витков медного провода. Диаметр провода 0,2 мм, диаметр соленоида – 5 см. По соленоиду течет ток 1 А. Определить, какое количество электричества протечет через обмотку, если концы ее замкнуть накоротко. Толщиной изоляции пренебречь.

Р е ш е н и е.

Количество электричества dq, которое протекает по проводнику за время dt при силе тока I, определяется равенством: dq = Idt. Общее количество электричества, протекшее через проводник за время t будет: q = .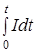

Сила тока в данном случае убывает экспоненциально со временем и выражается формулой: 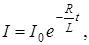где I ₀ - сила тока до замыкания, R - сопротивление обмотки соленоида, L - индуктивность соленоида.

Внося выражение для силы тока I под знак интеграла и интегрируя от 0 до ¥ (при t ®¥, I ® 0), получим:

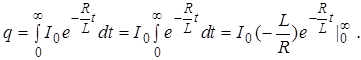
Подставим пределы интегрирования и определим количество электричества, протекающее через обмотку.

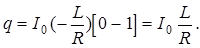(1)

Найдем L и R. Индуктивность соленоида

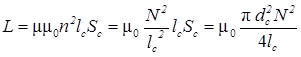. (2)

Сопротивление обмотки соленоида

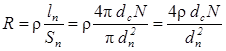(3)

Подставляя (2) и (3) в (1) и учитывая, что 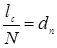, получим:

.

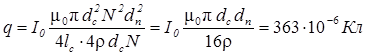4.2. ТРЕНИРОВОЧНЫЕ ЗАДАЧИ

1. Напряженность магнитного поля Н = 100 А/м. Вычислить магнитную индукцию В этого поля в вакууме. (Ответ. 126 мкТл).

2. По двум длинным проводам текут в одинаковом направлении токи I ₁ = 10 A и I ₂ = 15 A. Расстояние между проводами а = 10 см. Определить напряженность Н магнитного поля в точке, удаленной от первого провода на расстояние r ₁ = 8 см и от второго на r ₂ = 6 см. (Ответ. 44,5 А/м).

3. Решить задачу 2 при условии, что токи текут в противоположных направлениях. Точка удалена от первого провода на r ₁ = 15 см и от второго на r ₂ = 10 см. (Ответ. 17,4 А/м).

4. По тонкому проводнику, изогнутому в виде правильного шестиугольника со стороной а = 10 см, идет ток силой I = 20 А. Определить магнитную индукцию в центре шестиугольника. (Ответ. 138 мкТл).

5. Обмотка соленоида содержит два слоя плотно прилегающих друг к другу витков диаметром d = 0,2 мм. Определить магнитную индукцию В на оси соленоида, если по проводнику идет ток силой I = 0,5 А. (Ответ. 6,28 мТл).

6. В однородном магнитном поле с индукцией В = 0,01 Тл помещен прямой проводник длиной l = 20 см (подводящие провода находятся вне поля). Определить силу F, действующую на проводник, если по нему течет ток силой I = 5 А, а угол j между направлением тока и вектором магнитной индукции равен 30 ⁰. (Ответ. 50 мН).

7. Рамка с током силой I = 5 А содержит N = 20 витков тонкого провода. Определить магнитный момент р _m рамки с током, если ее площадь S = 10 см². (Ответ. 0,1 Ам²).

8. По витку радиусом R = 10 см течет ток I = 50 А. Виток помещен в однородное магнитное поле с индукцией В = 0,2 Тл. Определить момент силы М, действующей на виток, если плоскость витка составляет угол j = 60⁰ с линиями индукции. (Ответ. 0,157 Н м).

9. Протон влетел в магнитное поле перпендикулярно линиям индукции и описал дугу радиусом R = 10 см. Определить скорость v протона, если магнитная индукция В = 1 Тл. (Ответ. 9,57×10⁶ м/с).

10. Определить частоту n обращения электрона по круговой орбите в магнитном поле с индукцией В = 1 Тл. (Ответ. 2,8×10¹⁰с^-1).

11. Электрон в однородном магнитном поле движется по винтовой линии радиусом R = 5 см и шагом h = 20 см. Определить скорость v электрона, если магнитная индукция В = 0,1 мТл. (Ответ. 1,04×10⁶ м/с).

12. Кольцо радиусом R = 10 см находится в однородном магнитном поле с индукцией В = 0,138 Тл. Плоскость кольца составляет угол j= 30⁰ с линиями индукции. Вычислить магнитный поток Ф, пронизывающий кольцо. (Ответ. 5 мВб).

13. По проводнику, согнутому в виде квадрата со стороной а = 10 см, течет ток силой I =20 А. Плоскость квадрата перпендикулярна силовым линиям магнитного поля. Определить работу А, которую необходимо совершить для того, чтобы удалить проводник за пределы поля. Магнитная индукция В = 0,1 Тл. Поле считать однородным. (Ответ. 0,02 Дж).

14. Проводник длиной l = 1 м движется со скоростью v = 5 м/с перпендикулярно линиям индукции магнитного поля. Определить магнитную индукцию В, если на концах проводника возникает разность потенциалов U = 0,02 В. (Ответ. 4 мТл).

15. Рамка площадью S = 50 см², содержащая N = 100 витков, равномерно вращается в однородном магнитном поле (В = 40 мТл). Определить максимальную э.д.с. индукции e_max, если ось вращения лежит в плоскости рамки и перпендикулярна линиям индукции, а рамка вращается с частотой n = 96 об/мин. (Ответ. 2,01 В).

16. Кольцо из проволоки сопротивлением R = 1 мОм находится в однородном магнитном поле (В = 0,4 Тл). Плоскость кольца составляет угол j = 90⁰ с линиями индукции. Определить заряд q, который протечет по кольцу, если его выдернуть из поля. Площадь кольца S = 10 см². (Ответ. 0,4 Кл).

17. Соленоид содержит N = 4000 витков провода, по которому течет ток силой I = 20 А. Определить магнитный поток Ф и потокосцепление y, если индуктивность L = 0,4 Гн. (Ответ. 2 мВб. 8 Вб).

18. На картонный каркас длиной l = 50 см и площадью сечения S = 4 см² намотан в один слой провод диаметром d = 0,2 мм так, что витки плотно прилегают друг к другу (толщиной изоляции пренебречь). Определить индуктивность L получившегося соленоида. (Ответ. 6,28 мГн).

19. Определить силу тока в цепи через время t = 0,01 с после ее размыкания. Сопротивление цепи r = 20 Ом и индуктивность L = 0,1 Гн. Сила тока до размыкания цепи I ₀ = 50 А. (Ответ. 6,75 А).

20. По обмотке соленоида индуктивностью L = 0,2 Гн течет ток силой I = 10 А. Определить энергию W магнитного поля соленоида. (Ответ. 10 Дж).

4.3. ПРОВЕРОЧНЫЙ ТЕСТ

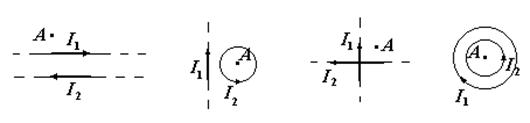
1. Указать все случаи, когда напряженность магнитного поля в точке А направлена за плоскость рисунка (I ₁ = I ₂).

1. 2. 3. 4.

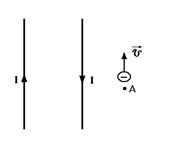
2. Поле создано двумя длинными параллельными проводами с то­ками I ₁ = I ₂ = I. Через точку А пролетает электрон. Как направлена сила, действующая на электрон?

Варианты ответа:

1) влево, 2) вправо, 3) к нам, 4) от нас

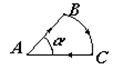
3. По контуру АВСА идет ток I = 12 А. Определить магнитную индукцию в точке А, если радиус дуги АВ = АС = 10 см, а угол a = 60⁰.

Дата добавления: 2014-12-16