Биномиальный закон распределения

Дискретной случайной величиной называется такая переменная величина, которая может принимать конечную или бесконечную совокупность значений, причем принятие ею каждого из значений есть случайное событие с определенной вероятностью.

Соотношение, устанавливающее связь между отдельными возможными значениями случайной величины и соответствующими им вероятностями, называется законом распределения дискретной случайной величины. Если обозначить возможные числовые значения случайной величины Х через , ,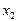... ...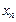, а через вероятность появления значения , то дискретная случайная величина полностью определяется следующей таблицей

			...
			...

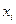
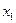
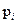
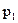
где значения , ,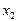... 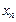записываются, как правило, в порядке возрастания. Таблица называется законом или рядом распределения дискретной случайной величины Х. Поскольку в верхней строчке ряда распределения записаны все значения случайной величины Х, то нижняя строчка обладает тем свойством, что

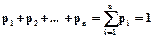
Графическое изображение ряда распределения называется многоугольником распределения (полигоном распределения) (рис. 4.1):

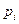
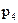
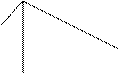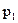
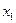
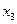
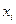
Для этого по оси абсцисс откладывают значения случайной величины, по оси ординат - вероятности значений. Полученные точки соединяют отрезками прямой. Построенная фигура и называется многоугольником распределения вероятностей.

Дискретная случайная величина может быть задана функцией распределения.

Функцией распределения случайной величины Х называется функция F (x), выражающая вероятность того, что Х примет значение, меньшее чем х:

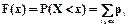
- здесь для каждого значения х суммируются вероятности тех значений 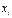, которые лежат левее точки х.

Функция F (x) есть неубывающая функция;

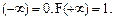
Для дискретных случайных величин функция распределения F(x) есть разрывная ступенчатая функция, непрерывная слева

Вероятность попадания случайной величины Х в промежуток от 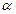до 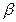(включая 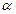) выражается формулой:

Случайная величина Х называется непрерывной, если ее функция распределения непрерывна и имеет производную.

Как уже было показано (формула 4.2), функцией распределения случайной величины Х называется функция F(x), выражающая вероятность выполнения условия :

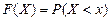
Функция распределения обладает следующими свойствами:

1.Вероятность попадания случайной величины в промежуток от 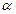до равна приращению функции распределения на концах этого промежутка:

так как вероятность любого отдельного значения случайной величины равна нулю, если функция распределения непрерывна при этом значении, т. Е.:

, когда F(x) - непрерывна в точке =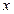

2.Функция распределения удовлетворяет условиям:

Плотностью распределения (дифференциальной функцией) непрерывной случайной величины называется функция

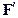f(x) = (x).

Плотность распределения любой случайной величины неотрицательна:

Несобственный интеграл от дифференциальной функции в пределах от - до + равен 1:

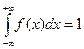
График функции y = f(x) называется кривой распределения или графиком плотности распределения. Кривая y = f (x) располагается над осью абсцисс.

Вероятность попадания случайной величины в промежуток от до может быть вычислена по формуле:

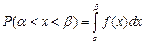
Подинтегральное выражение f(x)dx называется элементом вероятности. Оно выражает вероятность попадания случайной точки в промежуток между точками х и , где 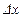бесконечно малая величина.

Функция распределения F(x) выражается через плотность f(x) формулой:

Математическое ожидание непрерывной случайной величины Х вычисляется по формуле:

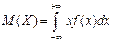
дисперсия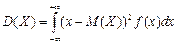

Математическим ожиданием дискретной случайной величины называется:

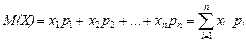
В случае бесконечного множества значений 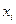в правой части находится ряд, и мы будем рассматривать только те значения Х, для которых этот ряд абсолютно сходится.

М(Х) представляет собой среднее ожидаемое значение случайной величины. Оно обладает следующими свойствами:

1) М(С)=С, где С=const

2) M (CX)=CM (X)

3) M (X+Y)=M(X)+M(Y), для любых Х и Y.

4) M (XY)=M (X)M(Y), если Х и Y независимы.

Для оценки степени рассеяния значений случайной величины около ее среднего значения M(X)= а вводятся понятия дисперсии D(X) и среднего квадратического (стандартного) отклонения 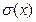. Дисперсией называется математическое ожидание квадрата разности (X- 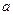), т.е.

где 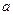= М(X); 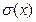определяется как квадратный корень из дисперсии, т.е. .

Для вычисления дисперсии пользуются формулой:

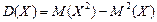
Свойства дисперсии и среднего квадратического отклонения:

1) D(C)=0, где С=сonst

2) D(CX)=C²D(X), 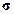(CX)= çCç 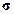(X)

3) D(X+Y) =D(X)+D(Y), 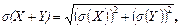если Х и У независимы.

Размерность величин 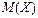и совпадает с размерностью самой случайной величины Х, а размерность D(X) равна квадрату размерности случайной величины Х.

Пусть случайная величина Х принимает значения с вероятностями 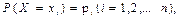а случайная величина Y- значения 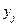с вероятностями 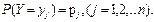Произведение КX случайной величины Х на постоянную величину К - это новая случайная величина, которая с теми же вероятностями, что и случайная величина Х, принимает значения, равные произведениям на К значений случайной величины Х. Следовательно, ее закон распределения имеет вид

			...
			...

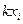
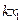
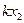
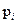
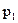
Квадрат случайной величины Х, т.е. , - это новая случайная величина,которая с теми же вероятностями, что и случайная величина Х, принимает значения, равные квадратам ее значений.

Сумма случайных величин Х и У - это новая случайная величина, которая принимает все значения вида 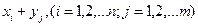с вероятностями 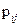, выражающими вероятность того, что случайная величина Х примет значение 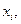а У - значение 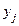, то есть

Если случайные величины Х и У независимы, то:

Аналогично определяются разность и произведение случайных величин Х и У.

Разность случайных величин Х и У - это новая случайная величина, которая принимает все значения вида 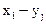, а произведение - все значения вида с вероятностями, определяемыми по формуле (4.8), а если случайные величины Х и У независимы, то по формуле (4.9).

Тема 5. «Законы распределения СВ»

Рассмотрим последовательность n идентичных повторных испытаний, удовлетворяющих следующим условиям:

1. Каждое испытание имеет два исхода, называемые успех и неуспех.

Эти два исхода - взаимно несовместные и противоположные события.

2. Вероятность успеха, обозначаемая p, остается постоянной от испытания к испытанию. Вероятность неуспеха обозначается q.

3. Все n испытаний - независимы. Это значит, что вероятность наступления события в любом из n повторных испытаний не зависит от результатов других испытаний.

Вероятность того, что в n независимых повторных испытаниях, в каждом из которых вероятность появления события равна , событие наступит ровно m раз (в любой последовательности), равна

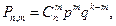
где q=1-р.

Вероятности того, что событие наступит:

а) менее m раз,

б) более m раз,

в) не менее m раз,

г) не более m раз - находятся соответственно по формулам:

Биномиальным называют закон распределения дискретной случайной величины Х - числа появлений события в n независимых испытаниях, в каждом из которых вероятность наступления события равна р; вероятности возможных значений Х = 0,1,2,..., m,...,n вычисляются по формуле Бернулли.

Число успехов Х=m				...	m	...	n
Вероятность				...		...

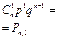
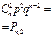
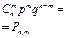
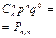
Так как правая часть формулы представляет общий член биноминального разложения 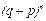, то этот закон распределения называют биномиальным. Для случайной величины Х, распределенной по биноминальному закону, имеем:

M(X)=nр

D(X)=nрq

Если число испытаний велико, а вероятность появления события р в каждом испытании очень мала, то пользуются приближенной формулой:

(*)

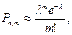где m - число появлений события в n независимых испытаниях, 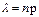(среднее число появлений события в n испытаниях).

Дата добавления: 2014-12-16